Временные системы в терминах «ВХОД — ВЫХОД»

Множество моментов времени. Первая часть первого пред­положения о характере функционирования систем гласит: систе­ма функционирует во времени. Множество моментов времени t, в которые рассматривается функционирование системы, обозначим Т, t ОТ. Множество T будем считать подмножеством множе­ства действительных чисел. В частности, оно может быть конечным или счетным. В зависимости от характера множества Т различают: дискретное, непрерывное и дискретно-непрерывное время. На практике часто представляют интерес только такие множества Т, элементы которых располагаются в изолированных точках числовой оси. В этом случае говорят, что система функционирует в дискретном времени, например контактные схемы, конечные автоматы, вычислительные устройства ЭВМ и т. д. Вместо моментов времени t₀, t_l , ... часто пишут ряд натуральных чисел 0, 1,2, ..., которые называются тактами.

Множество Т представляет собой множество некоторого (конечного или бесконечного) интервала числовой оси. В этом случае говорят, что система функционирует в непрерывном времени, например механические и электрические системы, системы, рассматриваемые в теории автоматического регулирования, и т. д.

Не исключены случаи, когда множество Т имеет дискретно-непрерывный характер: на одних, интервалах числовой прямой моменты t О Т заполняют их целиком, а на других — располагаются в изолированных точках. Например: 1) метеорологическая ракета при нахождении в состоянии готовности функционирует в непрерывном времени, а при запуске (при работе автомата пуска) можно условно считать, что работает в дискретном времени (реле времени работает дискретно в смысле выдачи команд исполнительным органом по тактам); 2) процесс производства автомобилей на конвейере; конвейер движется непрерывно, а готовые автомобили сходят с него в дискретные моменты времени.

Входные сигналы системы. Второе и третье предположения о характере функционирования систем направлены на описание взаимодействия системы с внешней средой. На вход системы могут поступать входные сигналы хОХ, где X — множество входных сигналов системы. Входной сигнал, поступивший в мо­мент времени te Т, обозначается x(t).

Возвратимся к примеру с выпуском предприятием однотипных изделий (часто их называют одно-продуктовое производство). В такой системе готовность в момент t, i-ro изделия (автомо­биля, часов, велосипеда, телевизора и т. д.) можно описать как поступление очередного сигнала x(t1) = 1. Здесь множество X сос­тоит из одного элемента х=1. Если принять за Х=0 сигнал, когда очередное изделие не готово, а за Х=1, когда оно готово, то можно считать, что Х={0, 1}, и в систему входной сигнал поступает в каждый момент tОТ. В случае, когда в моменты t1 оказываются готовыми одновременно несколько изделий (на заводе несколько конвейерных линий), например 0£ x£x_max, то множество X — совокупность целых чисел Х={О,1, ..., Хmax}.

Входные сигналы могут описываться некоторым набором ха­рактеристик. Например, если входными сигналами АСУ аэродромом считать самолеты, поступившие в зону аэродрома, то каждый из них может быть описан: 1) координатами точки взлета (I, a, e) (I-наклонная дальность, а - азимут и e - угол места); 2) вектором скорости (I, а, e); 3) признаками, характеризующими тип самолета (V), массу груза (G), требованиями к аэродромному обслуживанию (d) и т. д.

В общем случае будем предполагать, что входной сигнал X1ОXi, где X, — заданные множества (i= 1, n).

Прямое произведение X=X1´X2´.... ´.Хn называется пространством входных сигналов. Xi - элементарные оси, входной сигнал х представляет собой точку пространства X, описываемую координатами x1, x₂, ..., хn. В общем случае ХМХ.

При исследовании сложных систем приходится оперировать с группами входных сигналов, поступающих в моменты времени t_l<t₂<...<t_k. Будем предполагать, что множеству X принадлежит и пустой сигнал х_Ж, означающий отсутствие сигнала в момент t, x(t)=x_Ж.

Рассмотрим отображение x=L(t), сопоставляющее каждому tОТ некоторый сигнал хОX (отображение ¦: Т®Х). Обозначим через T^L множество моментов времени T^L М Т, такое, что для любого t^'О T^L справедливо L(t₁)№x_Ж. Отображение x=L(t) будем называть входным процессом систем, а совокупность упорядоченных пар (t^', х) для всех t^'О T^L (где x=L(t')) — входным сообщением.

Чтобы задать конкретный входной процесс x = L(t), достаточно указать соответствующее ему входное сообщение (t, x_l)_t.

Интервал времени t₁<t<t₂ будем обозначать (t₁,t₂), а полуинтервалы t_l<t<t₂ и t_l<t<t₂ — через (t₁,t₂] и [t₁,t₂), соответственно t_lЈtЈt₂ — через [t₁,t₂].

Введем понятие «сужение отображения». Пусть множество X имеет область определения отображения y=f(x). Отображение y=g(x) c областью определения X* является сужением отображения f(x) на множество X* в том и только в том случае, когда X*МX и g (x) =f(x) для каждого хОХ*.

Сужение отображения x=L(t) на множество TЗ(t₁,t₂] будем называть фрагментом входного процесса, соответствующим по­луинтервалу (t₁,t₂], а совокупность упорядоченных пар (t ', х) для всех t' ОT^LЗ(t₁,t₂), где x=L(t') — отрывком входного сообщения, поступающим в систему за полуинтервал (t₁,t₂] и обозначать (t₁,x_L]_t1^t2

Для конечного множества T^LЗ(t₁,t₂], например t₁,t₂,…,t_k, входное сообщение имеет вид

(t₁, х₁; t₂, х₂; ...; t_k, x_k).

Множество всевозможных входных сообщений обозначим {(t, x_L)_T}. Оно определяется множеством входных процессов вида x=L(t), допускаемых условиями функционирования системы. К множеству {(t, x_L)_T} будем причислять и пустое входное сообщение (t, x_L)_T = Ж, для которого T^L = 0.

Кроме того, множество {(t, x_L)_T} должно удовлетворять еще одному требованию, связанному с сочленением входных сообщений. Пусть (t, x_L1)_T и (t, x_L2)_T сообщения из множества {(t, x_L)_T}. Пусть, далее, t,<t₂<t₂; t_lt t₂, t₃ОТ. Образуем отрывки сообщений (t, x_L1]^t2_t1 и(t, x_L2]^t3_T2. Совокупность упорядоченных пар (t*, х*), где

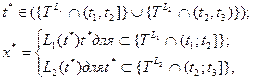можно рассматривать как отрывок (t, x_l]_t1^t3, некоторого сообщения (t, x_l-)_t, образовавшийся в результате сочленения отрывков (t,X_L1]^t3 и (t, x_L2]^t3_t2. Сочленение любого числа отрывков входных сооб­щений из множества {(t, x_l)_t] представляет собой отрывок некоторого входного сообщения, принадлежащего этому множеству.

Выходные сигналы системы. Система способна выдавать выходные сигналы yÎY, где Y — множество выходных сигналов системы. Выходной сигнал, выдаваемый системой в момент времени tÎТ, обозначается y(i).

Если выходной сигнал у описывается набором характеристик y₁, y₂, . . . y_m, таких, что уÎY_j, j=l, m, Y_j — заданные множества, то прямое произведение

Y=Y₁´ Y₂´ . . . ´ Ym

называется пространством выходных сигналов системы. По аналогии с входным процессом введем понятие выходного процесса y=N(t), а также определим выходное сообщение (t, y_N)_T и его отрывок (t, y_N]_t1^t2 на полуинтервале (t₁, t₂].

На этом можно считать исчерпанной формальную интерпретацию второго и третьего предположений о характере функционирования систем.

Глобальное состояние и глобальная реакция системы. Пусть для системы S множество ее состояний Z, а функция R: (X ´ Z) ® Y такова, что

(x, y) Î S Þ($_z)[R(x,y)=y.

Тогда Z называют множеством или объектом глобальных состояний системы, а элементы множества z Î Z — глобальными состояниями системы. Функция R называется глобальной реакцией системы S. При этом ни на Z, ни на R не налагается никаких дополнительных условий. В случаях, когда глобальную реакцию системы нельзя определить на всем произведении X х Z, то R оказывается частичной функцией. Таким образом, R можно называть глобальной реакцией системы только тогда, когда она не является частичной функцией. В противном случае ее называют частичной глобальной реакцией.

Абстрактные линейные системы. Хотя многие понятия теории систем можно определить, опираясь исключительно на понятие общей системы (3.1), получение содержательных математических результатов становится возможным только после введения дополнительных структур. Таким дополнительным понятием является понятие линейности систем.

Пусть А — некоторое поле, X и Y — линейные алгебры над А, S — отношение, SÌX´Y, причем S непусто. Пусть также

s Î S и s’Î S Þ s + s’ Î S

s Î S и a Î A Þ a_x Î S

где «+» обозначает (внутреннюю) операцию сложения в X´Y, а через а_x, обозначен результат (внешней) операции умножения на скаляр. Тогда S называется (абстрактной) полной линейной системой.

В соответствии с современной терминологией алгеброй называют множество вместе с некоторыми конечными операциями, а линейной алгеброй, в частное внутренней и одной внешней операциями, удовлетворяющими аксиомам векторного пространства. Операция «+» и умножения на скаляр определяются на X´Y естественным образом:

(x1,y1)+(x2,y2)=(x1+x2, y1+y2)

a(x,y)= (ax,ay)Ì X´Y, aÎA.

В теории линейных систем фундаментальную роль играет следующая теорема.

Пусть X и У — линейные алгебры над одним и тем же полем А. Система S ÌX´Y является линейной в том и случае, когда найдется такая глобальная реакция R : X´Я®Y, что

1. Z есть линейная алгебра над А;

2. существует пара таких линейных отображений

R1: Z®Y и R2: X ®Y,

что для всех (x,y) Î X´Y

R(x,z) = R1(x)+R2(z)

Отображение R называют линейной глобальной реакцией системы тогда, и только тогда, когда

1. R согласуется с S, т.е.

(x, y) Î S Þ($_z)[R(x,y)=y.

2. Z является линейной алгеброй над полем А скаляров линейных алгебр X и У.

Существуют два таких линейных отображений R1: Z®Y и R2: X ®Y, что для любых (x,y) Î X´Y

R(x, z) = R1(x)+R2(z)

В этом случае Z называют линейным объектом глобальных состояний системы, отображение R₁ : Z ® У — глобальной реак­цией на состояние, a R₂ : X ® Y — глобальной реакцией на вход.

Оглавление

Теоретико-множественное описание систем...................................

Предположения о характере функционирования систем...........

Система, как отношение на абстрактных множествах................

Временные, алгебраические и функциональные системы...........

Временные системы в терминах «ВХОД — ВЫХОД»...............

Формы представления модели

Традиционными формами представления моделей являются системы уравнений в нормальной форме Коши и нелинейные дифференциальные уравнения, графы, структурные схемы. Они позволяют описывать не иерархические модели.

Нормальная форма Коши

Единообразное по форме и удобное для использования матричного аппарата математическое описание динамических (обычно «гладких») систем достигается в пространстве состояний с использованием переменных состояния, т. е. уравнений в форме Коши

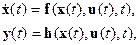(1.1)

где 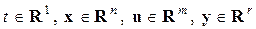векторы переменных состояния, управления и выходов; —  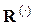 —  -мерное евклидово пространство; 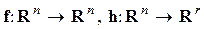гладкие отображения. Предполагается выполнение условия — их — существования решений, а для большинства практических задач единственности. Условия существования и единственности решений выполняются, если 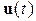принадлежит одному из следующих наиболее часто используемых классов функций: постоянные, кусочно-постоянные, кусочно-непрерывные, кусочно-гладкие, измеримые (локально-ограниченные), а функция 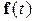удовлетворяет условиям Коши-Липшица — 

В работе [4] приводится классификация форм представления динамических моделей в терминах «вход-состояние-выход», являющихся частными случаями (1.1).

Билинейные системы

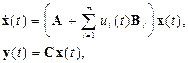
где 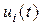скалярные функции, —  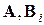числовые матрицы размеров —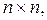 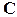 числовая матрица размера —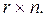 

L-системы

L-системой называется автономная невырожденная система вида

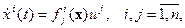
где 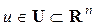, причем

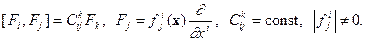
Здесь 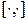является коммутатором алгебры Ли соответствующего векторного поля.

Линейные системы

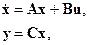
которые приводятся к L-системам 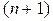-го порядка вида

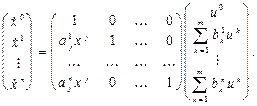
Линейно-аналитические системы

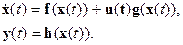
Если 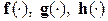полиномы, то система называется —  полиномиальной [132, 141, 161].

Системы с управлением, входящим линейно (правоинвариантные, аффинные) (векторное представление)

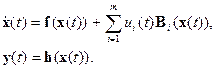
Системы управления с функциональными коэффициентами при переменных состояния и управления (матричное представление)

В ряде работ [43, 51, 52] принимается следующее описание

в векторно-матричной записи

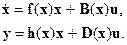
Переход от векторного к матричному представлению осуществляется с помощью интегрального преобразования [11]

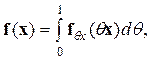
где 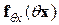матрица Якоби, найденная по —  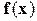из (1.12б).

Нормальная форма Коши (НФК) удобна для представления модели в алгорит­мах явного типа, и позволяет широко применять богатую матричную арифме­тику современных пакетов программ и библиотек языков программирования [1, 72, 86, 92, 96, 108].

К недостаткам данной формы представления необходимо отнести то, что в ней не сохраняется информации о топологии модели.