Лекция №6. Кибернетический подход к описанию систем

Управление как процесс. Кибернетический подход к описанию систем состоит в том, что всякое целенаправленное поведение рассматривается как управление. Управление — в широком, кибернетическом смысле — это обобщение приемов и методов, накопленных разными науками об управлении искусственными объектами и живыми организмами. Язык управления — это использование понятий «объект», «среда», «обратная связь», «алгоритм» и т.д.

U

Y

Y

X

субъект

объект

Среда

Под управлением будем понимать процесс организации такого целенаправленного воздействия на некоторую часть среды, называемую объектом управления, в результате которого удовлетворяются потреб ности субъекта, взаимодейст вующего с этим объектом.

рис. 2.1. Кибернетический подход кпроцессу управления

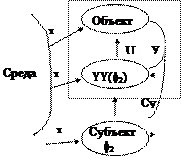
Анализ управления заставляет выделить тройку — среду, объект и субъект, внутри которой разыгрывается процесс управления (рис. 2.1). В данном случае субъект ощущает на себе воздействие среды Х и объекта У. Если состояние среды Х он изменить не может, то состоянием объекта У он может управлять с помощью специально организованного воздействия U. Это и есть управление.

Состояние объекта Y влияет на состояние потребностей субъекта. Потребности субъекта 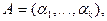где 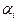— состояние i-й потребности субъекта, которая выражается неотрицательным числом, характеризующим насущность, актуальность этой потребности. Свое поведение субъект строит так, чтобы минимизировать насущность своих потребностей, т. е. решает задачу многокритериальной оптимизации:

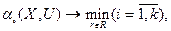(2.1)

где R — ресурсы субъекта. Эта зависимость выражает неизвестную, но существующую связь потребностей с состоянием среды Х и поведением U субъекта.

Пусть 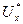—решение задачи (2.1), т. е. оптимальное поведение субъекта, минимизирующее его потребности А. Способ решения задачи (2.1), позволяющий определить 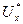, называется алгоритмом управления

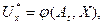(2.2)

где j — алгоритм, позволяющий синтезировать управление по состоянию среды Х и потребностей А_t,. Потребности субъекта изменяются не только под влиянием среды или объекта, но и самостоятельно, отражая жизнедеятельность субъекта, что отмечается индексом t.

Алгоритм управления j, которым располагает субъект, и определяет эффективность его функционирования в данной среде. Алгоритм имеет рекуррентный характер:

,

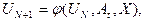т. е. позволяет на каждом шаге улучшать управление. Например, в смысле

,

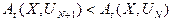т. е. уменьшения уровня своих потребностей.

Процесс управления как организация целенаправленного воздействия на объект может реализовываться как на интуитивном ,так и на осознанном уровне. Первый используют животные, второй — человек. Осознанное удовлетворение потребностей заставляет декомпозировать алгоритм управления и вводить промежуточную стадию — формулировку цели управления, т. е. действовать по двухэтапной схеме:

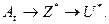
На первом этапе определяется цель управления 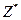, причем задача решается на интуитивном уровне:

,

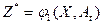где j₁ — алгоритм синтеза цели Z* по потребностям А_t и состоянию среды X. На втором этапе определяется управление 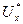, реализация которого обеспечивает достижение цели 2.*, сформированной на первой стадии, что и приводит к удовлетворению потребностей субъекта. Именно на этой стадии может быть использована вся мощь формального аппарата, с помощью которого по цели Z* синтезируется управление

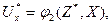
где j₂ — алгоритм управления. Этот алгоритм и есть предмет изучения кибернетики как науки.

Таким образом, разделение процесса управления на два этапа отражает известные стороны науки — неформальный, интуитивный, экспертный и формальный, алгоритмизуемый. Если первая

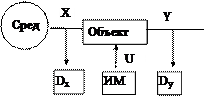
Ряс. 2.2. Взаимодействие Рис. 2.3. Структурная схема

элементов системы управления. системы управления

пока полностью принадлежит человеку, то вторая является объектом приложения формальных подходов. Естественно, что эти различные функции выполняются разными структурными элементами. Первую функцию (, выполняет субъект, а вторую ( — управляющее устройство (УУ). На рис. 2.2 показано взаимодействие этих элементов. Штриховой линией выделена система управления (СУ), выполняющая функцию реализации целей управления 2*, формируемых субъектом.

Системы управления сложный объект управления •. Структурная схема СУ приведена на рис. 2.3. Здесь Dx и Dy — датчики, измеряющие состояние среды и объекта соответственно. Результаты измерений Х'=Dx(Х) и У'=Dy(У) образуют исходную информацию ]= {X', У'} для УУ, которое на этой основе вырабатывает команду управления и, являющуюся лишь информациейо том, в какое положение должны быть приведены управляемыевходы объекта. Следовательно, управление (/ есть результатработы алгоритма

.

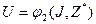Как видно, управление в широком смысле образуется четверкой

{ .}

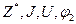В качестве примера рассмотрим основные понятия управления в технических и организационных системах.

Управление — целенаправленная организация того или иного процесса, протекающего в системе. В общем случае процесс управления состоит из следующих четырех элементов:

n получение информации о задачах управления (Z*),

n получение информации о результатах управления (т. е. о поведении объекта управления У’);

n анализ полученной информации и выработка решения (J=={х'. У'}),

n исполнение решения (т. е. осуществление управляющих воз-

действий и').

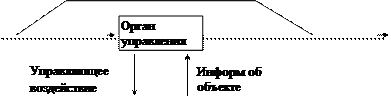
Процесс управления — это информационный процесс (рис.2.4), заключающийся в сборе информации о ходе процесса, передаче ее в пункты накопления и переработки, анализе поступающей, накопленной и справочной информации, принятии решения на основе выполненного анализа, выработке соответствующего управляющего воздействия и доведении его до объекта управления. Каждая фаза процесса управления протекает во взаимодействии с окружающей средой при воздействии различного рода помех. Цели, принципы и границы управления зависят от сущности решаемой задачи.

Система управления — совокупность взаимодействующих между собой объекта управления и органа управления, деятельность которых направлена заданной цели управления (рис2.5).

Итрормациснная связь с АСУ Полее Высокого уровня

+

			Выходной материальный поток
	Входной материальный поток

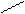
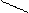
Рис. 2.4. Процесс управления как информационные процесс

(рис. 2.5). В СУ решаются четыре основные задачи управления: стабилизация, выполнение программы, слежение, оптимизация.

Задачами стабилизации системы являются задачи поддержания ее выходных величин вблизи некоторых неизменных заданных значений, несмотря на действие помех. Например, стабилизация напряжения U и частоты f тока в сети вне зависимости от изменения потребления энергии.

Задача выполнения программы возникает в случаях, когда заданные значения управляемых величин изменяются во времени заранее известным образом.

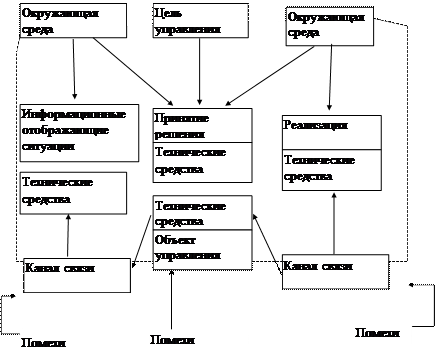
Рис. 2.5. Системы управления как совокупность объектов

В системах оптимального управления требуется наилучшим образом выполнить поставленную перед системой задачу при заданных реальных условиях и ограничениях. Понятие оптимальности должно быть конкретизировано для каждого отдельного случая.

Прежде чем принимать решение о создании СУ, необходимо рассмотреть все его этапы, независимо от того, с помощью каких технических средств они будут реализованы. Такой алгоритмический анализ управления является основой для принятия решения о создании СУ и степени ее автоматизации. При этом анализе следует обязательно учитывать фактор сложности объекта управления:

n отсутствие математического описания системы;

n стохастичность поведения;

n негативность к управлению;

n не стационарность, дрейф характеристик;

n невоспроизводимость экспериментов (развивающаяся система все время как бы перестает быть сама собой, что предъявляет специальные требования к синтезу и коррекции модели объекта управления).

Особенности сложной системы часто приводят к тому, что цель управления таким объектом в полной мере никогда не достигается, как бы совершенно ни было управление.

Системы управления делятся на два больших класса: системы автоматического управления (САУ) и автоматизированные системы управления (АСУ). В САУ управление объектом или системой осуществляется без непосредственного участия человека автоматическими устройствами. Это замкнутые системы. Основные функции САУ: автоматический контроль и измерения, автоматическая сигнализация, автоматическая защита, автоматические пуск и остановка различных двигателей и приводов, автоматическое поддержание заданных режимов работы оборудования, автоматическое регулирование. В отличие от САУ в АСУ в контур управления включен человек, на которого возлагаются функции принятия наиболее важных

решений и ответственности за принятые решения. Под АСУ обычно понимают человеко-машинные системы, использующие

современные экономико-математические методы, средства электронно-вычислительной техники(ЭВТ) и связи, а также новые организационные принципы для отыскания и реализации на практике наиболее эффективного управления объектом(системой).

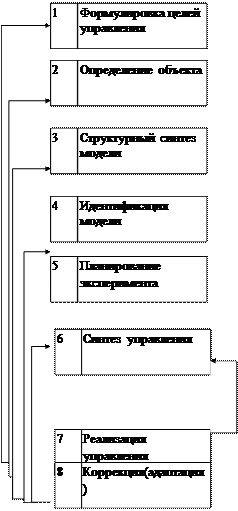
Этапы управления. Управление сложной системы состоит из этапов, представленных на рис.2.6.

1. Формирование цепей. Множество целей управления, которое должно реализовать СУ определяется как внешними по отношению к системе, так и внутренними факторами и, в частности, потребностям субъекта А. Сложность формализации учета влияния на цели очевидна. Различают три вида целей: стабилизация— заключается в требовании поддерживать выходы объекта на заданном уровне; ограничение — требует нахождения в заданных границах целевых переменных 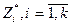; экстремальная цель—сводится к поддержанию в экстремальном состоянии целевых переменных .

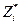2. Определение объекта управления. Этот этап связан с выделением той части среды субъекта, состояние которой он может изменить и тем самым воздействовать на свои потребности. В ряде случаев, когда границы объекта очевидны, проблемы выделения объекта из среды не возникает. Это бывает, когда объект достаточно автономен (самолет, телефонная станция и т. д.). Однако в других случаях связи объекта со средой настолько сильны и разнообразны, что порой очень трудно понять, где кончается объект и начинается среда. Именно это и заставляет вводить специальный этап — определение объекта управления. Объект должен быть в определенном смысле минимальным, т. е. иметь наименьший объем. Это необходимо с целью минимизации трудоемкости его изучения при синтезе модели. При этом существенным ограничением выступает достижимость множества целей управления {Z*} в рамках выделенного для этого ресурса R. Это означает, что для любого состояния среды Х должно найтись управление 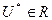, с помощью которого можно добиться любой допустимой цели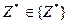

3. Структурный синтез модели. Последующие три этапа управления сложными системами связаны с решением задачи создания ее модели, которая нужна для синтеза управления U. Только с помощью модели объекта можно построить управление U*, переводящее объект в требуемое (целевое) состояние Z*. Модель F, связывающая входы Х и U с выходом У, определяется структурой SТ и параметрами С={с1 ...,ck}, т. е. представима в виде двойки F={SТ, С). На этом этапе определяется структура SТ, т. е. модель объекта с точностью до значений ее параметров С. Этап структурного синтеза включает: определение внешней структуры модели, декомпозицию модели, определение внутренней структуры элементов модели. Синтез внешней структуры сводится к содержательному определению входов Х и U, выхода У без учета внутренней структуры объекта, т. е. объект рассматривается как некий «черный ящик» с n+q входами и m выходами. Декомпозиция модели заключается в том, чтобы, воспользовавшись априорными сведениями о структуре объекта, упростить задачу синтеза структуры модели. Синтез структуры модели сводится к определению вида оператора F модели объекта с точностью до параметров С. Это значит, что параметры становятся переменными модели, т. е.

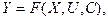(2.3)

где F — оператор преобразования структуры SТ, параметры которого для удобства внесены в переменные С. Представление оператора преобразования модели в виде (2.3) можно назвать параметризацией модели, что эквивалентно заданию его структуры. При синтезе структуры моделей объектов управления могут применяться различные подходы — от классических методов теории автоматического управления (ТАУ) до современных методов имитационного моделирования (методы случайного поиска, статистических испытаний и др.), семиотического моделирования с использованием языка бинарных отношений и других методов современной математики, использующих сочетание дополняющих друг друга возможностей аналитических и статистических, семиотических и графических и других формализованных представлений системы.

4. Идентификация параметров модели объекта. Этот этап связан с определением числовых значений параметров С в режиме нормального функционирования объекта. Делается это стандартными приемами идентификации. Для выяснения зависимости выхода объекта от управляемых входов (U необходимо преднамеренно их изменять, т. е. экспериментировать с объектом. Однако сложная система «не любит» эксперименты, нарушающие режим ее нормального функционирования. Поэтому эксперимент, которого нельзя набежать, следует проводить, минимально возмущая объект, но так, чтобы получить при этом максимальную информацию о влиянии варьируемых параметров на выход объекта.

5. Планирование эксперимента. На данном этане главным является синтез плана эксперимента, позволяющего с максимальной эффективностью определить искомые параметры модели объекта управления. Для статического объекта этот план {U представляет собой набор состояний управляемого выхода объекта U={U1 ..., Un}, а для динамического — план-функцию 0<=t<=T, т. е. программу изменения во времени входа объекта. Эксперимент на объекте дает возможность определить реакцию объекта на это воздействие. В статическом случае эта реакция имеет вид Y={y1, ..., yn), где 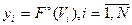, а в динамическом — У(1)= ^{и(1)}. Полученная информация и является исходной для определения параметров модели F: У=F(U, С), что осуществляется методами идентификации. План эксперимента 0 определяется: структурой SТ модели F, ресурсом планирования R, который образуется выделяемыми на эксперимент средствами, областью планирования, определяющей пределы изменения входа U; критерием планирования, который определяет эффективность плана U.

6. Синтез управления. На этом этапе принимается решение о том, каково должно быть управление (U, чтобы достигнуть заданной цели управления Z* в объекте. Это решение опирается на имеющуюся модель объекта F, заданную цель Z*, полученную информацию о состоянии среды Х и выделенный ресурс управления R, который представляет собой ограничения, накладываемые на управление (U в связи со спецификой объекта и возможностями СУ. Достижение цели Z* возможно соответствующим выбором управления U (состояние среды Х изменяется независимо от нас). Это приводит к экстремальной задаче

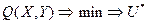
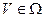
решение которой U* является оптимальным управлением. Способы решения задачи (2.4) существенно зависят от структуры модели объекта F. Если объект статический, т. е. F— функция, то получаем задачу математического программирования, если же —динамический, т. е. F— оператор, то решают вариационную задачу.

7. Реализация управления или отработка в объекте оптимального решения U*, полученного на предыдущем этапе. Реализовав управление и убедившись, что цель управления не достигнута, возвращаются к одному из предыдущих этапов. Даже в лучшем случае, когда поставленная цель достигнута, необходимость обращения к предыдущему этапу вызывается изменением состояния среды Х или сменой цели управления U*.

Таким образом, при благоприятном стечении обстоятельств обращаются к этапу синтеза управления (стрелка а на рис. 2.6), где определяется новое состояние, которое отражает новую ситуацию, сложившуюся в среде. Так функционирует стандартный контур управления простым объектом.

8. Адаптация. Специфика управления сложной системой состоит в том, что благодаря зашумленности и нестационарности информация, полученная на предыдущих этапах, приближенно отражает состояние системы лишь в предыдущие моменты времени. Это и вызывает необходимость коррекции. Коррекция может затрагивать различные этапы.

Простейшая коррекция связана с подстройкой параметров модели С (стрелка с, рис. 2.6). Такого рода коррекцию называют адаптацией модели, а управление — адаптивным управлением. Если управление U не обеспечивает необходимого разнообразия входа объекта для эффективной коррекции параметров модели, то приходится принимать специальные меры планирования эксперимента путем добавления специальных тестовых сигналов (стрелка Ь, рис. 2.6). Такое управление называют дуальным. Однако одной коррекции параметров модели может оказаться недостаточно, если изменилась ее структура. Поэтому время от времени необходима коррекция структуры модели, т. е. приведение ее в соответствие с новой информацией (стрелка d, рис. 2.6).

Далее коррекция может коснуться самого объекта, точнее, границы разделения объекта и среды. Это бывает необходимо призначительном изменении (эволюции) объекта и окружающей ее среды (стрелка е, рис. 2.6). И наконец, созданная СУ по ряду причин может не реализовать все множество целей управления, в результате необходима адаптация целей (стрелка g, рис. 2.6).

Очевидно, что не все из описанных выше восьми этапов управления присутствуют при синтезе СУ. В ряде случаев некоторые из них выпадают. Например, объект управления может быть выделен из среды и тогда нет необходимости в этапе планирования эксперимента, так как модель объекта проста и все ее параметры можно определить без специально организованного эксперимента.

Оглавление

Лекция №6. Кибернетический подход к описанию систем............

Лекция №7. Алгоритмы на топологических моделях.

Алгоритмы на топологических моделях. Представление графов в ЭВМ. Матрицы смежности, изоморфности, достижимости и контрдостижимости, списочные формы. Алгоритмы на графах. Алгоритмы поиска путей, выделения контуров, поиск касающихся контуров.

6.1. Задачи анализа топологии

Под топологическим анализом понимается выявление структурных свойств и особенностей модели на основании исследования моделей первого ранга неопределенности Ms(1), т.е. на основании информации о взаимосвязи переменных графа.

К основным задачам анализа топологии, относятся задачи поиска путей, выделения контуров, декомпозиции на подсистемы.

Алгоритмы для такого анализа на основании представлений моделей в форме графов или матричной форме неоднократно приводились в литературе [6, 28, 107]. Традиционные постановки касаются в основном линейных систем, составленных из однонаправленных элементов.

Алгоритмы топологического анализа имеют огромное значение для исследования СС НСУ с помощью ЭВМ, так как проблема повышения эффективности по быстродействию и точности существующих методов моделирования может быть решена за счет более полного учета топологических особенностей модели [45, 46, 124, 126].

Пример вычисление передаточных функций системы по формуле Мезона.

Расписать пример.

6.2. Представление информации о топологии моделей

Представление топологии модели возможно в списочной и матричной форме. При организации программных средств чаще используется списочная форма. При больших размерностях одноуровневых сильно разряженных моделей она имеет преимущества по требуемой памяти и скорости работы алгоритмов топологического анализа. Однако для сильно связанных систем небольшой размерности или иерархических систем эффективнее испробовать алгоритмы, основанные на матричных формах, например на матрицах смежности.

В качестве иллюстрации на рис. 1.1. приведена диаграмма графа модели странного аттрактора Лоренца [93]. Эта форма представления позволяет эффективнее решать задачи выделения путей и ко­нтуров, связности, структурной управляемости и многие другие, чем в форме НФК и отчасти СНДУ.

Модель системы представляется ориентированным графом H=<G,H> с множеством переменных Х=x₁, .... , x_n, N - общее множество вершин, и множеством дуг G - упорядоченных пар номеров смежных вершин (i,j), G=(i,j)1, ... (i,j)n. Общее количество таких пар обозначено в приме­рах как Q.

Несмотря на всю компактность и удобство такой записи, на практике чаще используют матрицу смежности R = r_ij, показывающую наличие дуги между i-ой и j-ой вершинами.

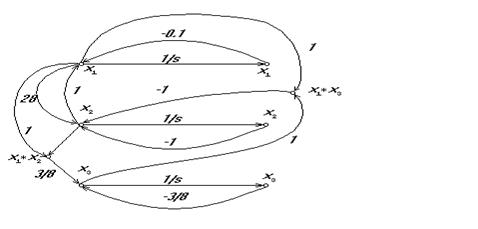
Рис. 2.1. Модель странного аттрактора в форме ориентированного графа

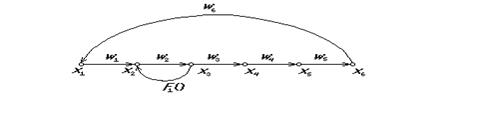
Рис. 2.2. Модель системы в форме графа

Другим способом представления топологии является матрица изоморфности D, в строках которой представлены номера входящих (с плюсом) и выходящих (с минусом) дуг.

Для приведенного на рис. 2.2 примера матрицы смежности и изоморфности имеют вид:

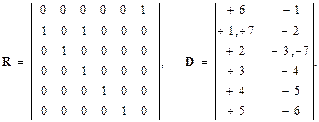
Избыточность хранимой информации в матрице смежности (нулевые значения) компенсируют­ся простотой вычислительных алгоритмов и скоростью получения требуемой ин­формации из матрицы. Кроме того, наличие только двух значений 0 или 1, дает возможность использовать для ее представления битовые поля, что дает значительную экономию памяти, и при размерах системы порядка 100 элементов не уступает по затратам ресурсов на хранение матрицы изоморфности, при значительно более простых алгоритмов обработки информации. Использование матриц смежности, инцидентностей, достижимостей и др. имеет большое применение для алгоритмов топологи­ческого анализа СС НСУ [107].

Ориентированные графы (структурные схемы) обычно широко используются при описании линейных систем и систем с одновходовыми нелинейностями. Однако возникают некоторые затруднения при описании нелинейных систем, где нелиней­ные функции могут зависеть от нескольких переменных, например при описании операций умножения и деления.

6.3. Переборные методы

6.4. Поиск контуров и путей по матрице смежности

Наиболее простым способом идентификации путей и контуров являются матричные алгоритмы структурного анализа [107]. Они строятся на основе последовательного возведения в соответствующие степени матрицы смежности (см. 1.5).

Единица в матрице смежности S говорит о наличии пути между i‑й и j-й вершинами длиной 1. Наличие 1 в (i, j)-й позиции в матрицы 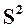означает путь длиной 2 между этими вершинами, и так далее. Таким образом, существование ненулевого значения на главной диагонали означает наличие пути из дан­ной вершины в данную вершину, длинна которого равна степени матрицы. Значение матрицы смежности в раз­личных степенях для графа, представленного на рис. 3.1 показаны ниже:

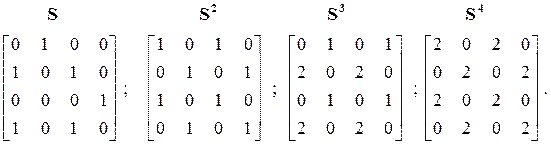
Наличие 1 в главной диагонали 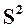указывает на то, что четыре переменные сис­темы входят в контуры длиной 2. Это позволяет определить вершины, вхо­дящие в контуры, его длину, но не конкретный вид. Поэтому требуется уточняющий переборный алгоритм на отобранных вершинах нелинейного системного гибридного графа, определя­ющего конкретный вид контура известной длины. На выходе этого алгоритма формируется дополняемый список из номеров вершин, входящих в каждый контур. С учетом различной длины контуров его удобнее представлять в памяти ПЭВМ динамическим списком

.

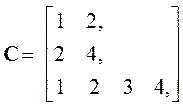Четвертая степень матрицы смежности 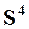содержит информацию об еще одном контуре длиной 4. Но кроме этого повторяется информация о кон­турах длиной 2.

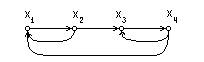
Рис. 3.1. Диаграмма графа одноуровневой модели СУ

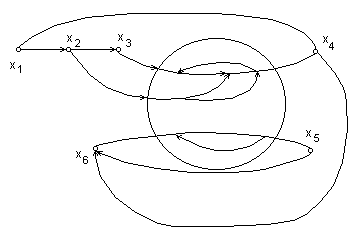
Рис. 3.2. Диаграмма графа иерархической модели СУ

Отмеченные особенности этого метода, повторение ин­формации о контурах в матрицах более высокого порядка, кратного длине контура; трудности в обработки контуров одинаковой длины, требуют применения, в дополнению к рассматриваемому методу переборного алгоритма, уточняющего и отбрасывающего повторяющую информацию.

Наиболее существенным недостатком данного метода является его низкое быстродействие в следствие большого количества возведений матрицы смежности в соответствующие степени и большие затраты памяти ЭВМ для хранения информации.

6.5. Модифицированный алгоритм поиска контуров и путей по матрице смежности

Недостатки алгоритма поиска путей и контуров на основании представления топологии модели в форме матриц смежности, отмеченные выше, могут быть компенсированы, если использовать логические операции вместо математических и побитовое представление матрицы смежности. Быстрый рост необходимой памяти и временных затрат на работу алгоритма с ростом размерности систем в предлагаемом алгоритме компенсируются иерархическим представлением топологии модели а так же иерархическим характером построения алгоритмов топологического анализа.

Реализация алгоритма в этом случае использует не умножение, а логическую операцию И (в матрице присутствуют только значения 0 и 1), выполняемую одной машинной командой.

Как отмечалось ранее, составной характер представляемых моделей требует учета наличия связей между входами и выходами внутри подсистем. С этой целью водится матрица существования связи:

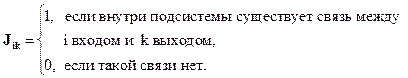(3.1)

Пример, иллюстрирую­щий данную особенность показан на рис. 3.2. При формировании матрицы смежности информация о внутренних контурах подсистемы не учитывается, учитывается только информация матрицы J (3.1) существования связи между входами и выходами подсистемы. Возве­дение в соответствующие степени матрицы смежности S позволяет выделить для данной системы 3 контура.

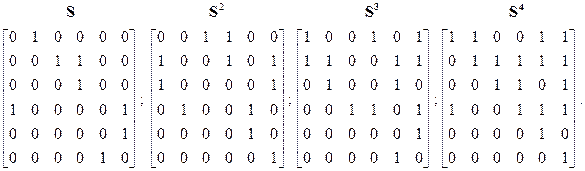
Логическая сумма, - операции ИЛИ - позволяет определить все возмож­ные связи между вершинами.

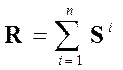(3.2)

где n - размерность системы и, кроме того, определяет длину макси­мально возможного пути. Данную сумму называют матрицей достижимости.

Транспонированная матрица достижимости

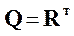, (3.3)

называемой матрицей контрдостижимостей.

Ниже приведены значения матриц достижимости и контрдостижимос­ти для системы представленной на рис. 3.2.

.

Если в матрице достижимости оставить только входные и выходные вершины подсистемы данного уровня иерархии, то получится матрица связей J (3.1), которая должна быть передана в вышестоящую по уровню систему для составления аналогичных функций структур­ного анализа и учета этой информации на стадии моделирования.

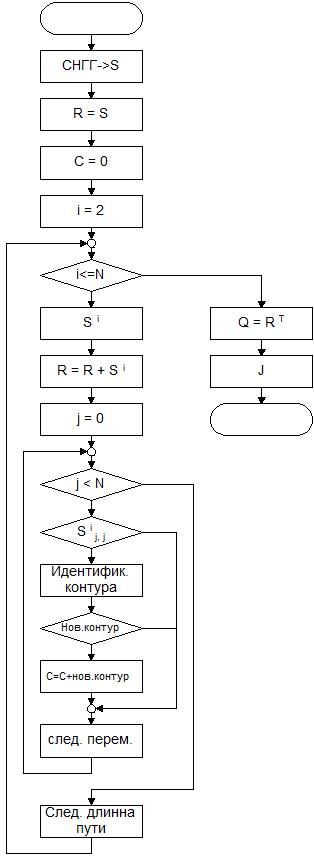
Блок схема, реализующая предлагаемый алгоритм, показана на рис. 3.4. Блок 1 выполняет преобразование из внутренней формы представления нелинейного системного гибридного графа в матрицу смежности размером N * N. Блоки 3 и 4 задают начальные значения матриц контуров С и достижимости R. Блоки 4,5,15 организуют основной цикл. Блок 6 вычисляет i-ю степень матрицы смежности, перемножение выполняется логической операцией “И”. Блок 7 выполняет накопление информации о всех возможных путях в матрице достижимости, суммирование производится ло­гической операцией “ИЛИ”. Блоки 8,9,14 организуют цикл проверки вершин на принадлежность к контурам. В этом цикле перебираются элементы глав­ной диагонали матрицы 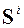. Если вершина j относится к контуру, длиной i (блок 10), то в блоке 11 переборными методами этот контур выделяется. Выделенный контур, в блоке 12, сравнивается с уже существующими, хра­нящимися в списке контуров С. Если контур новый, то он добавляется к списку (блок 13). После завершения основного цикла, вычисляется матри­ца контрдостижимости Q (блок 16) и матрица связей в системе (подсистеме) J (блок 17), после чего алгоритм завершает свою работу. Выходными параметрами, возвращаемыми в вызвавшую программу, являются матрицы R,Q, J, C.

S= 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 S 2 = 0 0 1 0 0 0 0 0 0 1 1 0 1 1 0 0 0 1 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 S 3 = 0 0 0 1 1 0 1 1 0 0 0 1 0 1 1 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 S 4 = 1 1 0 0 0 1 0 1 1 0 0 0 0 0 1 1 1 0 1 1 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 0 S 5 = 0 1 1 0 0 0 0 0 1 1 1 0 1 1 0 1 1 1 0 1 1 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 S 6 = 0 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0 1 0 0 1 1 1 0 0 1 1 0 0 0 0 0 0 0 0 0

Рис. 3.4. Блок-схема и пример работы программы выделения контуров

6.6. Поиск контуров и путей по матрице изоморфности

6. 5. Диаграмма графа

Матрица изоморфности D

-1
-2
-3
		-4
	-8
	-5	-6	-9
	-7

Алгоритм идентификации контуров следующий:

1. Просмотреть строки матрицы. Для i-й строки просмотреть элементы до обнаружения отрицательного элемента D_{i j} <0. Запомнить номер строки и значение элемента D_{i j}.

2. Найти строки в матрице содержащие элемента D _{k l} == - D_{i j}. Для каждой найденной строки выполнить пп. 1, до тех пор пока в найденной последовательности повторно не вертится уже обнаруженная дуга, или программе не удастся обнаружить новую дугу, выходящую из этой вершины.

Пример для графа, представленного на рис. 6.5.

1. В 0-й строке нашел D[0][0]= -1 ;

2. Нашел D[1][1]= 1 ;

3. Â 1-é строке нашел новый отрицательный элемент D[1][0] = -2 ;

4. Нашел D[2][1]= 2 ;

5. В 2-й строке нашел новый отрицательный элемент D[2][0] = -3 ;

6. Нашел D[3][0] = 3 ;

7. Â 3-é строке нашел новый отрицательный элемент D[3][2] = -4 ;

8. Нашел D[4][0]= 4 ;

9. Â 4-é строке нашел новые отрицательные элементы D[4][1] = -5, D[4][1] = -6, D[4][1] = -9. Необходимо разветвить поиск ;

10. Нашел D[3][1]= 5 ;

11. Â 3-é строке нашел отрицательный элемент D[3][2] = -4. Этот элемент уже был в цепочки поиска. Поиск по этой ветки прекращен. Возвращаемся в пп.9 ;

12. Нашел D[1][2]= 6 ;

13. Â 1-é строке нашел отрицательный элемент D[1][0] = -2. Этот элемент уже был в цепочки поиска. Поиск по этой ветки прекращен. Возвращаемся в пп.9 ;

14. Нашел D[6][0]= 9 ;

15. Â 6-é строке нашел новый отрицательный элемент D[6][1] = -7 ;

16. Нашел D[0][1]= 7 ;

17. В 0-й строке нашел D[0][0]= -1. Этот элемент уже был в цепочки поиска. Поиск по этой ветки прекращен.

18. Новых отрицательных элементов в матрице не осталось поиск прекращен.

После завершения поиска имеем:

-1	-2	-3	-4	-8		-5	-4
						-6	-2
						-9	-7	-1

По данным этого списка составляем контура.

Обычно в литературе указывается на высокую эффективность данного алгоритма. Он дейс<