Метод расчета фазовых состояний углеводородных систем. Константы равновесия. Вывод уравнения равновесия фаз. Решение уравнений фазового равновесия.

Наибольшее распространение как у нас, так и за рубежом получил метод определения констант равновесия по атласу NGAA, выпущенному американской ассоциацией газобензинового производства. Атлас содержит константы равновесия от метана до декана включительно, а также азота и углекислоты. Константа равновесия при данном давлении схождения определяется по атласу, исходя из данных значения давления и температуры. При расчетах на ЭВМ использования графиков констант равновесия затруднительно, т.к. приходится многократно снимать с графиков значения констант и вводить их в память ЭВМ. В связи с этим атласа NGAA переведены в таблицы:

Рекомендации по автоматизации выбора констант равновесия углеводородных систем на ЭВМ. Таблицы констант равновесия. ВНИИ газ, Москва, 1972 г. Частично атлас констант равновесия представлен в справочнике: Катц, «Добыча и транспорт газа».

Уравнения равновесия фаз.

Для расчетов нужны следующие исходные данные:

- начальное давление пласта

- начальная температура пласта

- состав углеводородной системы

- константы равновесия отдельных составляющих компонентов, К=y/x, где

y-молярная доля компонента в газовой фазе,

x-молярная доля компонента в жидкой фазе, находящейся в равновесии с газовой фазой.

Каждому компоненту смеси при данных температуре и давлении соответствуют свои константы равновесия. Определяются они экспериментальным путем. Зависимости константы равновесия выражаются через приведенные параметры:

, , .

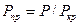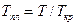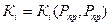В случае многокомпонентной смеси критическое давление называют давлением схождения. Так как в критической и закритической области нет различия между жидкостью и паром (газом), то для смеси:

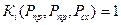
Давление схождения соответствует определенному составу смеси и является числовой характеристикой состава.

Атлас констант составлен для широких пределов изменения Р_сх.

Для многокомпонентной смеси составляется уравнение фазовых концентраций. N – масса всех компонентов в некотором объеме V. N_Г – масса компонентов в газе, N_ж – масса компонентов в жидкости N = N_Г +N_Ж.

Если разделить на сумму молекулярных масс всех компонентов, содержащихся в объеме V, получим n_М = n_МГ + n_МЖ – число молей компонентов, газовой и жидкой фазе.

Молярная доля компонентов в газе «y_i» и в жидкости «x_i»:

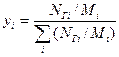
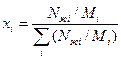
N_Гi – масса i-го компонента в газовой фазе

N_жi – масса i-го компонента в жидкой фазе

M_i – молекулярная масса i-го компонента

Молярная доля i-го компонента в объеме в целом выражается:

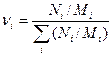
N_i – масса i-го компонента в объеме V.

Из приведенных выражений следует: (*)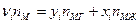

Обозначим:

n_МГ/n_М = Y – мольная доля всех компонентов в газовой фазе.

n_МЖ/n_М = X – мольная доля всех компонентов в жидкой фазе

Учитывая y_i = K_ix_i? 1=X+Y, подставим в равенство (*)

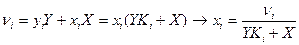
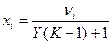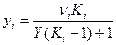
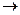, Уравнения фазовых концентраций

При определении фазового состояния могут решаться различные задачи.

Например, даны: ν_i (состав), P,T,Y → тогда определяют x_i и y_i из ур-ий концентраций. Чаще возникает задача отыскания Y,X по известному составу ν_i , P,T. Тогда используется равенство 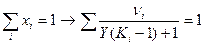. Уравнение решается итерационным методом. Исходное уравнение решается в виде: .

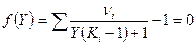Очевидно, что при Y=0 f(Y)=0.

Максимальное значение доли газовой фазы Y=1. следовательно решение отыскивается в интервале 0<Y<1. для применения Ньютона (касательных) используется производная функция f(Y): .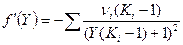

Приняв за начальное приближение Y₀=0.5 и применяя последовательно итерационные формулы метода Ньютона – метода хорд, находят решение при малом количестве итераций:

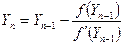
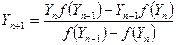
Двухфазная фильтрация.

В связи с проектированием и анализом разработки нефтяных и газовых месторождений приходится исследовать совместное течение в пористой среде нескольких жидкостей, чаще всего воды, нефти и газа, представляющих собой обособленные фазы, не смешивающихся между собой.

Формирование залежей происходит в результате оттеснения находившейся там первоначально воды. Поэтому вместе с нефтью и газом в коллекторах находится некоторое количество (10-30%) погребенной воды. Кроме того, многие залежи заполнены нефтью, газом только в верхней купольной части, а нижележащие зоны заполнены не оттесненной в процессе формирования водой с первоначальным ее содержанием. Самые верхние части залежи содержат газ, который может находится изначально, или собираться в процессе разработки. Двух или трехфазное течение возникает при разработке нефтяных залежей, нефтегазовых, газоконденсатных и просто газовых при наличии подстилающей газовую шапку воды, т.е. практически всегда, исключая сухие газовые ловушки.

При фильтрации двух жидкостей (нефть-вода), или жидкости и газа (нефть-газ, вода-газ) закон Дарси имеет другой вид, чем при однофазной ф-ии:

,

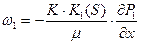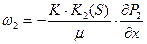
Здесь K₁(S)? К₂(S) – относительно фазовые проницаемости, зависящие от S – насыщенность 2-й фазы, обычно воды, 1-я фаза – нефть и газ.

В гидродинамических расчетах часто удобно пользоваться эмпирическими зависимостями значений относительной фазовой проницаемости от насыщенности, полученными из экспериментальных данных. Рассмотрим эмпирические формулы, полученные Чень-Чжун-Сяном, которые можно применять при оценочных расчетах.

1. Для воды и нефти (s-водонасыщенность):

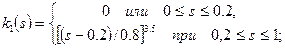
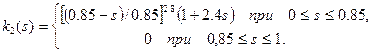
2. для газа и воды (s-газонасыщенность):

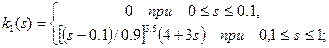
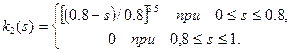
Поведение относительных фазовых проницаемостей описывается графиками вида:

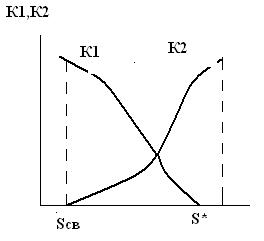
Зависимости имеют две характерные точки S_св, S_*

В точке S=S_св относительная проницаемость воды = 0 = К₂(S)

В точке S=S_* относительная проницаемость нефти (газа) = 0

К₁(S) = 0

В этих точках фаза с нулевой проницаемостью диспергирована и занимает разрозненные тупиковые места в пористой среде, поэтому не подвижна. Одновременная фильтрация 3-х фаз изучена менее чем двухфазная. Пользуются таким приемом. S_н +S_в = S_ж, рассматривая 2 фазы – жидкую и газовую S_Г +S_ж=1 двухфазная система.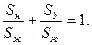

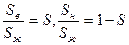двухфазная система, К_н(S), К_в(S)

K_Г(S_ж), К_ж(S_ж)

Все относительные проницаемости определяются по двухфазным диаграммам, (S_Г, S_ж) и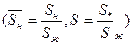

Тогда относительная проницаемость для нефти – К_ж(S_ж)К_н(S)

для воды - К_ж(S_ж)К_в(S)

для газа – К_Г(S_ж)

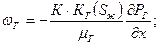
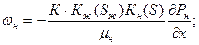
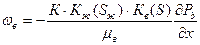
Для пластов большой толщины, или наклонных пластов, где необходимо учитывать гравитацию, если ось Z, то вертикальная составляющая скорости фильтрации двух-трехфазной вместо 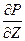содержит:

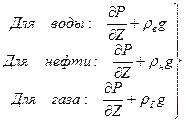P – одинаковые давления в фазах.

P^* = P + ρgZ приведенные давления.

Мы рассмотрели выражения скорости фильтрации для двух, трехфазного фильтрационного потока. Если движутся две или три несмешивающиеся фазы (нефть, газ, вода) то такого же вида уравнения будут, записаны для каждой в отдельности:

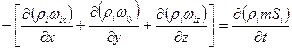
I=1, 2, 3 где 1-газ

2 – нефть

3 – вода или: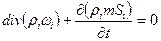

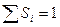
Отличие от уравнения неразрывности однофазной жидкости – в уравнение входят 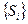- насыщенности фаз. В левой части S_i влияют на фазовые проницаемости. В правой части при составлении баланса масс для элемента мы должны учитывать для отдельной фазы не весь объем пор, а его долю, занимаемую i-ой фазой.

Если в систему уравнений неразрывности фаз подставить выражения скоростей, как функций давления и насыщенности, а также выражения плотностей фаз как функций давления, то для системы 3-х уравнений имеем неизвестных 4-Р, S₁,S₂,S₃.

Система замыкается соотношением: S₁ + S₂ + S₃ = 1.

В данном случае предполагалось, что давления в фазах одинаковы Р.

Капиллярные силы. В поровых каналах возникают силы межфазного (капиллярного) давления, например в двухфазном течении.

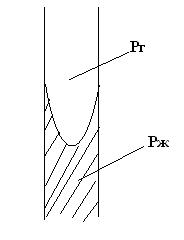
Р_г – Р_ж = Р_k(S_ж)

Так как функции Р_k(S_ж) изучены экспериментально, то ввод кап. сил в уравнение не прибавляет количества неизвестных.

7. Многофазная многокомпонентная фильтрация. Трехфазная – двух-трехмерная фильтрация.

Рассматривается система из "n_l" фаз, например:

1-я фаза – нефть, смачивающая по газу, несмачивающая по воде;

2-я фаза – вода, смачивающая;

3-я фаза – газ, несмачивающая.

В целом система состоит из "n_c" химических компонентов. При движении, изменении давления, температуры смеси отдельные углеводородные компоненты могут переходить из нефтяной фазы в газовую и наоборот. Не исключается переход воды в газообразное состояние, при термическом воздействии на пласт. Между фазами происходит массообмен различными компонентами. В этом случае материальный баланс при выводе уравнения неразрывности записывается для каждого компонента в отдельности, и в результате имеем "n_c" уравнений неразрывности.

Доля порового пространства элемента сетки, занятая "1"-ой фазой – S₁;

С_еj – концентрация j – го компонента в 1 – фазе в рассматриваемом объеме сетки.

Тогда изменение массы j – го компонента в элементе сетки необходимо рассматривать как сумму его изменений в каждой фазе, учитывая (S₁· С_еj) – доля порового объема элемента, занятая j – ым компонентом в 1 – ой фазе;

S_l·C_lj·ρ_l – массовая доля j – го компонента в поровом объеме элемента сетки 1 – ой фазе;

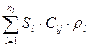- общая массовая доля j – го компонента в поровом объеме элемента сетки 1 – ой фазе;

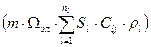- массовая доля j – го компонента в поровом объеме элемента сетки;

Ω_эл – объем элемента сетки.

Изменение массы j – го компонента за малый промежуток времени Δt, в случае декартовой системы координат, запишем виде:

.

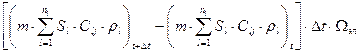Пусть 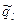- плотность источника (стока) 1 – ой фазы, 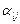- концентрация j – го компонента в источнике 1 – ой фазы.

Тогда 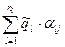- общая плотность источника по j – ой компоненте.

Потоковые слагаемые в уравнении неразрывности, в отличие от однофазного движения, содержат

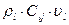- массовая скорость j – го компонента в потоке 1 – ой фазы.

В уравнении материального баланса j – го компонента суммируются перетоки рассматриваемого компонента по всем фазам.

В результате уравнение неразрывности для j – го компонента имеет вид:

.

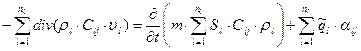Количество уравнений системы определяется количеством движущихся компонент j=1,2,…,n_c.

Трехфазная модель нефтяного пласта.

При проектировании нефтяных пластов широкое применение получила модель нелетучей нефти (бета-модель). Углеводородная система аппроксимирована двумя компонентами: нелетучим (нефтью) и летучим (газом), растворимым в нефти. Предполагается, что в пористой среде сосуществуют три отдельные фазы: нефть, газ и вода.

Вода и нефть не смешиваются, не обмениваются массами и не меняют фаз.

Газ растворим в нефти, нерастворим в воде.

Предполагается термодинамическое равновесие флюидов при постоянной температуре.

Рассмотрим движение трехфазного флюида: нефть, газ, вода (г, н, в):

газовая фаза состоит из одного компонента – свободного газа;

водная фаза – из одного водного компонента;

нефтяная фаза – 2-х компонент, нефти и растворенного в ней газа.

Определим концентрации компонент в фазаз;1,2 – нефть, газ.

С_Н1 – концентрация нефти в нефтяной фазе;

С_Н2 - концентрация газа в нефтяной фазе;

С_В1 = С_В2 = 0, т.е. водная фаза не содержит компонент газа и нефти;

С_Г2 = 1, т.е. в газовой фазе содержится только газ;

С_lj – массовая концентрация j – го компонента в 1 – ой фазе.

Рассмотрим левую часть уравнения неразрывности многофазного флюида.

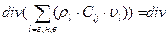(суммы по всем фазам потоков j – го компонента).

Введем понятие объемных коэффициентов фаз: отношение объема фазы в пластовых условиях к объему в стандартных условиях.

Для газовой фазы:

.

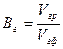Для водной фазы:

.

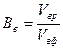Для нефтяной фазы:

,

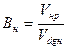здесь 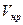- объем нефти в пластовых условиях с учетом растворенного в ней газа;

где 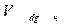- объем дегазированной нефти в н.у.

Введем понятие растворимости газа в нефти, определяя коэффициент растворимости R:

,

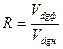где 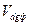- объем газа, растворенного в нефти при н.у.

Рассмотрим уравнение неразрывности для газового компонента, движущегося в газовой и нефтяной фазе.

Массовая скорость свободного газа:

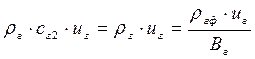
Массовая скорость газа, растворенного в нефти:

,

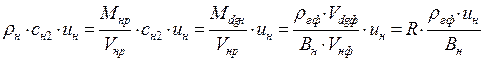где 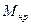- масса нефтяной фазы в рабочих условиях;

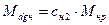- масса газа, растворенного в нефтяной фазе в рабочих условиях.

Итак, в левой части уравнения неразрывности для газового компонента:

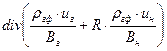
В правой части:

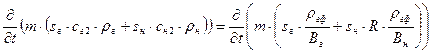
Учитывая наличие источников (стоков), уравнение неразрывности для газового компонента в виде:

,

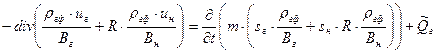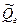- масса газа, отбираемая из единицы объема.

Для компонент, не содержащих растворенного газа:

,

.

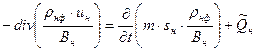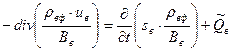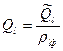- объемы фаз, отбираемые в стандартных условиях.

Учитывая, что газ отбирается как из свободного компонента газа, так и из нефти:

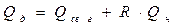
уравнение неразрывности β – та модели в объемных единицах:

;

;

.

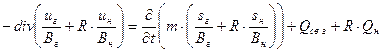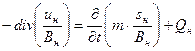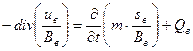СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

Основная литература

Дополнительная литература

1. Лысенко В. Д.Инновационная разработка нефтянных месторождений. - М.:Недра-Бизнесцентр,2000. - 516с. - Библиогр.: с.513-514

2. Закиров, С. Н. Разработка газовых, газоконденсатных и нефтегазоконденсатных месторождений / С.Н. Закиров. - М. : Струна, 1998. - 626 с. - Библиогр.: с. 597-620. - ISBN 5-85926-011-3

3. Желтов, Ю. П. Разработка нефтяных месторождений : учебник для вузов / Ю. П. Желтов. - 2-е изд., перераб. и доп. - М. : Недра, 1998. - 365 с. : ил. - Библиогр. с. 359. - ISBN 5-247-03806-1

4. Каневская Р.Д. Математическое моделирование гидродинамических процессов разработки месторождений углеводородов. - М.- Ижевск: Институт компьютерных исследований, 2002. - 140 с.