Лекция 2. Математические модели естественных режимов разработки. Основы теории упругого режима. Точные и приближённые решения уравнения пьезопроводности.

Если пласт замкнутый, эксплуатируется при упругом режиме, то добыча нефти за период падения, средневзвешенного давления Р₀ - 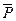составит упругий запас

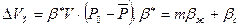
C другой стороны, отобрано жидкости за время t:

q·t

Уравнение баланса: q·t = .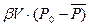

Если рассматривать малый период "dt", взять дифференциал баланса: ,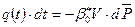

получим дифференциальное уравнение: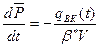

Рассмотрим нефтяную залежь, окруженную водным бассейном. Законтурную область плоскорадиальной фильтрации воды от удаленного контура R_∞ до контура нефтеносности залежи R_к представим как замкнутую. Тогда для неё аналогичное уравнение материального баланса, как для замкнутого контура нефтяной залежи:

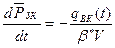
здесь 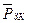- средневзвешенное давление законтурной области;

q_ВК (t) – расход воды в нефтяную залежь.

Приняв приближенно фильтрацию воды в водном бассейне стационарной по Дюпюи:

,

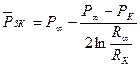получим:

,

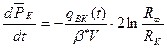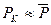
Пусть нефтяная залежь эксплуатируется при водонапорном режиме с притоком воды через контур нефтеносности. Тогда исходный баланс:

q·t = .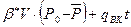

Так, упругий баланс составит:

.

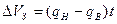Дифференциальное уравнение материального баланса:

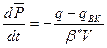
В этом случае падение давления меньше, чем для замкнутого пласта.

Идентификация модели.

Если замкнутый контур эксплуатируется при упругом режиме, уравнение истощения:

,

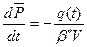где V - объём пласта,

β* - упругоемкость,

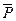- средневзвешенное давление.

Падение давления за время t = 0 до момента t:

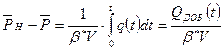или ,

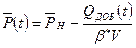т.е. прямая линия при ,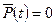

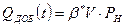
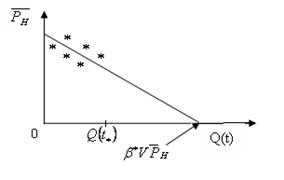
Коэффициент "β^*V" в уравнении истощения нельзя определить точно по данным геолого-физических исследований. Если имеются данные истории эксплуатации месторождения от t = 0 до t = t_* замеров:

t₁ { ~ }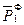

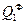t₂ { ~ }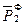

- - - - - - - - -

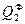t_* { ~ }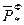

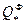то методом наименьших квадратов находят коэффициент 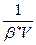в уравнении, а следовательно, полный упругий запас нефти .

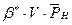Так по фактическим данным истории эксплуатации уточняются коэффициенты уравнений, описывающих процесс разработки, т.е. моделей разработки.

Задача. Уточнение коэффициентов моделей разработки по фактическим данным месторождений называется идентификацией модели. Решение этой задачи необходимо для обеспечения надежности прогнозирования.

Рассмотрим уравнение разработки нефтяной залежи, когда в неё вторгается законтурная вода, т.е. упруговодонапорный режим:

,

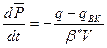q_ВК – дебит законтурной воды в залежь.

.

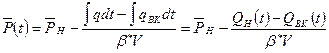В данном уравнении неизвестных 2 - .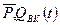

Для замыкания системы используется уравнение Ван-Эвердингена, притока воды в разрабатываемую залежь при упруговодонапорном режиме с применением метода суперпозиций.

Изменение давления на контуре важно знать для прогнозирования времени перехода месторождения с упруговодонапорного на режим растворенного газа, а затем на газонапорный. Особенно это важно для нефтей с высоким содержанием парафина.

Кроме того, важно знать, в течение какого времени можно разрабатывать залежь без воздействия на пласт заводнением.

При водонапорном режиме залежь взаимодействует с водным бассейном и необходимо определить объемы поступающей в залежь воды, динамику давления на контур залежи.

При исследовании проявления водонапорного режима газовая залежь часто аппроксимируется укрупненной скважиной. На теории укрупненной скважины основаны методики прогнозирования показателей разработки при водонапорном режиме. Кроме того, на её основе предложены методики уточнения параметров водоносного пласта.

Теория укрупненной скважины Ван-Эвердингена и Херста.

Первый вариант.

Допустим залежь – укрупненная скважина радиусом R_З, эксплуатируется в водоносном бассейне с постоянным во времени расходом воды "q_В", поступающей в залежь.

Согласно решению Ван-Эвердингена и Херста, изменение во времени давления на контуре укрупненной скважины Р(R_З) определяется по следующему уравнению:

.

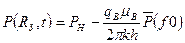Здесь:

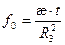- параметр Фурье;

h, k и æ – толщина и коэффициентыпроницаемости и пьезопроводности;

μ_В – динамическая вязкость;

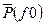- табулируемая функция.

Второй вариант.

Пусть залежь – укрупненная скважина, эксплуатируется с постоянным во времени перепадом давления на водоносный пласт:

ΔР = Р_Н – Р(R_З).

Для вычисления суммарного количества воды, которое поступит в залежь к моменту t, Ван-Эвердингеном и Херстом получено выражение:

,

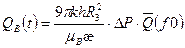где 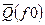- табулированная функция.

В первом варианте известна динамика вторжения воды в залежь в виде зависимости дебита укрупненной скважины от времени, q_B(t). Необходимо найти давление на контуре укрупненной скважины к моменту t, т.е. .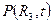

Период времени от начала t₀ до t, разбиваем на n отрезков, т.е. t= n Δt. Для любого i – го отрезка, 1 ≤ i ≥ n, известно приращение дебита воды:

.

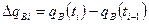В начальный момент t₀ полагаем 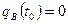, тогда:

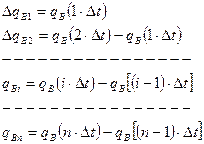
Элементарные дебиты 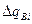рассматриваются как последовательно включающиеся, и далее постоянно действующие на пласт за период .

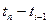Метод суперпозиций дает решение, получающееся в результате суммарного действия всех элементарных дебитов 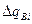как сумму решений от действия каждого 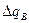а отдельности в период 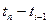. Очевидно, что, суммируя все 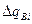, к моменту 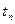получим, что на пласт действует 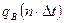, т.е. 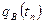, т.к. величина каждого последующего 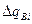погашает действие предыдущего 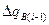. Тогда давление на контуре залежи при 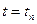получается суммированием:

.

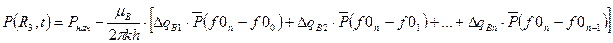
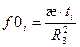Вариант 2.

Допустим, во втором варианте известно изменение давления на контуре укрупненной скважины, 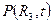, необходимо определить приток воды в залежь к моменту времени t, т.е. .

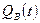Интервал времени разбивается на n отрезков Δt, т.е. t= n Δt. Для любого i – го отрезка, 1 ≤ i ≥ n, известно падение давления на контуре укрупненной скважины:

.

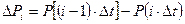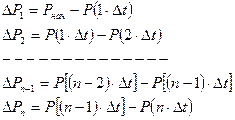
Здесь Р_нач – давление в начальный момент времени t₀.

Согласно принципу суперпозиций общий приток воды в залежь складывается из суммы решений, полученных от действия на водоносный пласт каждого перепада 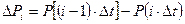как постоянного, начиная со времени .

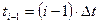Тогда общий приток воды складывается из суммы притоков от каждого постоянного перепада 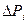в соответствии с периодом действия этого перепада к моменту t, начиная с :

- - - - - - - - - - - - - - - - - - - - - - - - - -

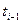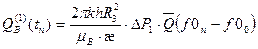
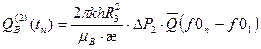
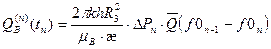
Общий приток воды за период 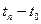в результате последовательного снижения давления от Р_н до Р_n получается суммированием:

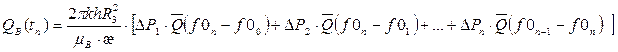
Для расчета показателей разработки нефтяного пласта методом материального баланса составляется система из уравнения материального баланса для залежи нефти, эксплуатируемой в водоносном пласте, и формулы притока воды. При этом давление на контуре скважины уравнивается с средним давлением в залежи.

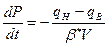
или в интегральной форме:

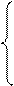
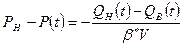
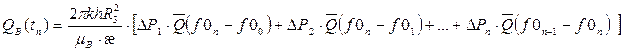
Система решается по шагам 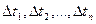относительно неизвестных 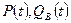при условии, что на предыдущих шагах времени известны 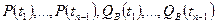, а также известно на начало: 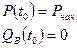, где .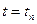

Подставляя 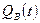в первое уравнение системы, получим линейное уравнение относительно .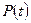