Однородные дифференциальные уравнения

Дифференциальное уравнение называется однородным, если оно может быть представлено в виде

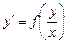. (1)

Например, уравнение

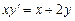
– однородное. Действительно, разделив обе части на x, получим

.

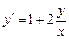Однородное уравнение решается подстановкой

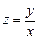. (2)

Из (2) следует 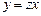, 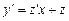. Подставляя в уравнение (1), получаем

,

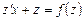или

.

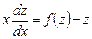Мы получили уравнение с разделяющимися переменными

.

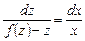Возьмем интеграл от обеих частей; обозначим

.

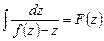Получаем

.

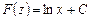Сделаем обратную замену:

.

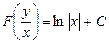Это общий интеграл уравнения (1).

Пример. Решить уравнение .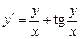

Решение. 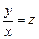, 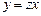. Получаем

.

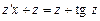Отсюда

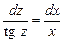, или .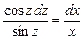

Интегрируя, получаем общий интеграл

.

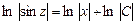Здесь, впрочем, нетрудно выразить y, т.е. получить общее решение (для , , ).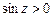

.

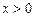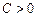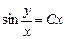
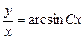
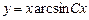8.2. Дифференциальные уравнения второго
порядка

Дифференциальное уравнение второго порядка имеет вид

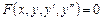(1)

или

.

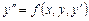В некоторых случаях дифференциальное уравнение второго порядка может быть сведено к последовательному решению двух дифференциальных уравнений первого порядка. В этом случае говорят, что данное дифференциальное уравнение допускает понижение порядка.

Общим решением дифференциального уравнения (1) называется функция

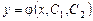, (3)

существенно* зависящая от двух произвольных постоянных и обращающая уравнение (1) в тождество при любых значениях этих постоянных.

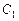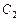Решения, которые получаются из общего решения при фиксированных значениях и , называются частными.

(Существуют также решения, не содержащиеся в общем решении ни при каких 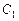и 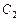. Такие решения называются особыми. Мы не будем рассматривать особые решения.)

Понижение порядка дифференциального
уравнения

Рассмотрим частные виды уравнения (1), когда это уравнение допускает понижение порядка.

1. Уравнение не содержит искомой функции y, т.е. имеет вид

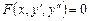. (4)

В этом случае достаточно сделать замену

.

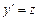Тогда 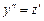и уравнение (4) принимает вид

,

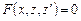т.е. является уравнением первогом порядка относительно z.

Найдем его общее решение

.

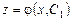Сделаем обратную замену

.

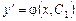Отсюда получаем

.

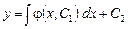Пример. Решить уравнение .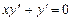

Решение. Положим 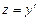. Тогда 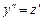и исходное уравнение принимает вид 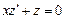, или 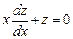, откуда

.

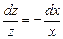Интегрируя, получим

.

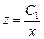Произведя обратную замену, получаем

.

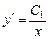Решая последнее уравнение, получаем

.

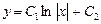2. Уравнение не содержит в явном виде аргументаx:

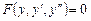. (5)

В этом случае порядок уравнения можно понизить, если положить 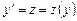. Тогда

.

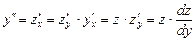Пример. Решить уравнение .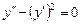

Решение. Заменой 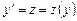сводим данное уравнение к уравнению первого порядка

.

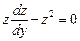
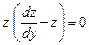Первое решение этого уравнения z = 0, или y = C, где C = const. Далее получаем

.

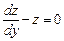Разделяя переменные и интегрируя, получаем

.

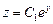Произведем обратную замену:

.

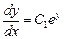Здесь также переменные разделяются:

.

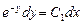
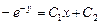Так как 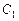и 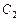– произвольные постоянные, то можем написать (взяв 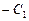вместо 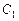и 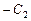вместо )

.

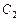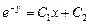
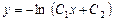Очевидно, это решение включает в себя и решение y = C, полученное выше.

Линейные дифференциальные уравнения второго
порядка с постоянными коэффициентами

Линейным дифференциальным уравнением называется такое дифференциальное уравнение, в которое неизвестная функция y и ее производные 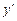, , 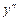... входят линейно, т.е. в первых степенях, не перемножаясь между собой.

Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид

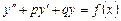, (1)

где p, q = const.

Если 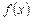тождественно равна нулю, то уравнение

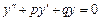(2)

называется однородным, в противном случае – неоднородным. (Принято говорить также, что уравнение (2) есть однородное уравнение, сопутствующее уравнению (1).)

Выясним структуру общего решения однородного дифференциального уравнения (2).

Начнем с определения. Две функци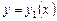и и 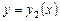называются линейно независимыми на отрезке 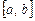, если их отношение на этом отрезке не является постоянной величиной, т.е. если

.

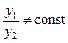В противном случае функции называются линейно зависимыми.

Например, функци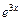и и 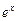линейно независимы, так как .

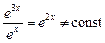Легко показать, что 1) если 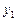есть решение уравнения (2), то для любой постоянной C функция 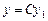также есть решение уравнения (2) и 2) есл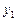и и 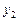– решения уравнения (2), то их сумма 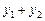– также есть решение уравнения (2). На этом основано следующее утверждение.

Теорема. Есл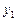и и 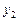– два линейно независимых решения дифференциального уравнения (2), то общее решение уравнения (2) есть функция

,

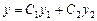где .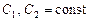

Итак, чтобы найти общее решение уравнения (2), надо найти два его линейно независимых частных решения 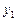и .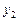

Выясним, какой должна быть функция y, которая при подстановке ее в уравнение (2) превращает его в тождество. Левая часть уравнения (2) есть сумма самой функции y и ее производных 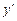и 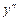, взятых с некоторыми постоянными коэффициентами. Чтобы такая сумма оказалась тождественным нулем, надо, чтобы y, 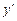и 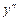были подобны между собой. Известно, что функция 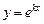подобна своим производным. Действительно, 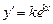, 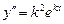. Будем искать частные решения уравнения (2) в виде 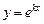. Подставим эту функцию в левую часть уравнения (2). Получим

,

.

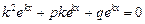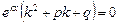Так как 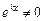, то

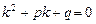. (3)

Уравнение (3) называется характеристическим уравнением для дифференциального уравнения (2).

Итак, для того чтобы функция 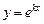была решением дифференциального уравнения (2), надо, чтобы k было корнем алгебраического уравнения (3).

Из алгебры известно, что при решении квадратного уравнения (3) могут встретиться 3 случая:

I. Корни уравнения (3) действительные и различные.

II. Корни уравнения (3) действительные и совпадают.

III. Уравнение (3) не имеет действительных корней.

Случай I. Пусть корни уравнения (3) действительны и различны: 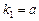, , 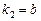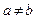. Тогда дифференциальное уравнение (2) имеет решение 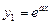, 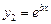. При этом

.

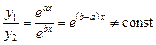Примеры: 1) 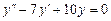. Характеристическое уравнение 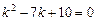. Его корни 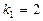, 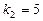. Поэтому общее решение дифференциального уравнения есть

.

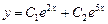2) 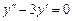. Здесь характеристическое уравнение имеет вид 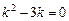. Его корни 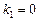, 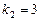. Поэтому общее решение есть

.

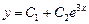Случай II.Корни характеристического уравнения (3) совпадают: 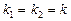. Очевидно, 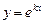будет в этом случае решением дифференциального уравнения (2). Но второго частного решения 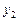, имеющего аналогичный вид 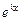, и такого, чтобы 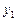и 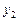были линейно независимы, найти не удается. Однако в этом случае можно доказать, что решением уравнения (2) будет также

.

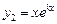Итак, в случае, когда корни характеристического уравнения (3) совпадают 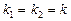, общее решение дифференциального уравнения (2) есть

.

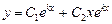Пример. 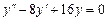. Характеристическое уравнение , .

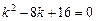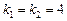Общее решение:

.

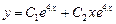Случай III.Характеристическое уравнение (3) не имеет действительных корней.

В этом случае корни уравнения (3) – мнимые: 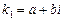, 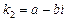(где i – мнимая единица, 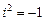). Находят их по формулам 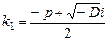, , 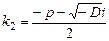где D – дискриминант, или, что то же самое,

, .

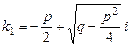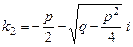Можно доказать, что в случае, когда корни уравнения (3) мнимые: 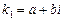, , 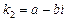общее решение уравнения (2) имеет вид

.

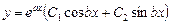Примеры: 1) .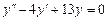

Характеристическое уравнение: 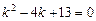. Его корни: 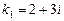, 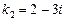. Общее решение:

;

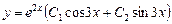2) .

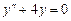Характеристическое уравнение: 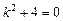. Корни: 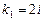, 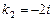. Общее решение:

.

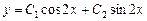Итак, мы рассмотрели все три случая. Заметим, что при решении однородного дифференциального уравнения с постоянными коэффициентами мы не применяли интегрирование, а пользовались только корнями алгебраического уравнения (3).

Перейдем теперь к неоднородным уравнениям. Нас интересует структура общего решения линейного неоднородного уравнения (1).

Теорема. Если 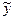– какое-нибудь частное решение дифференциального уравнения

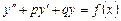, (1)

а 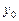– общее решение его сопровождающего однородного уравнения

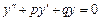, (2)

то их сумма

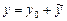(4)

будет общим решением дифференциального уравнения (1).

Доказательство.Подставим функцию (4) в левую часть уравнения (1). Получим

,

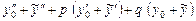или, что то же самое,

.

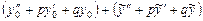Так как 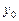– решение (2), то 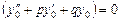, а так как 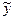– решение (1), то 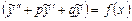. Итак, функция (4) есть решение уравнения (1). Надо еще убедиться, что решение (4) – общее. Но 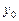, являясь общим решением уравнения (2), существенно зависит от двух произвольных постоянных, поэтому решение (4) зависит от (тех же) двух произвольных постоянных. Следовательно, решение (4) – общее. Теорема доказана.

Итак, нахождение общего решения неоднородного линейного дифференциального уравнения сводится теперь к нахождению какого-нибудь его частногорешения.

Рассмотрим способы нахождения частного решения неоднородного линейного дифференциального уравнения для некоторых видов правой части.

Дано уравнение

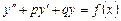. (1)

I. Пусть 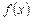– многочлен степени n: 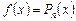. Нетрудно убедиться в том, что при 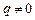частным решением этого уравнения будет также многочлен и степень его также равна n: .

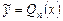Если же q = 0, то (так как степень многочлена понижается при дифференцировании на единицу) частное решение будет многочленом степени n + 1: 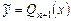. При этом оказывается, что 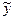можно искать в виде 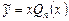, т.е. в виде многочлена (n + 1)-й степени со свободным членом, равным нулю.

Аналогично, при q = 0, p = 0 частное решение 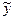надо искать в виде .

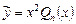Коэффициенты многочлена 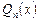находят методом неопределенных коэффициентов.

Пример 1. Рассмотрим дифференциальное уравнение

.

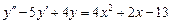Здесь 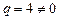, следовательно, 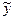ищем в виде многочлена второй степени: 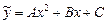. Имеем 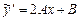, 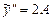. Подставим 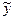и ее производные в уравнение:

,

.

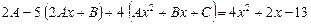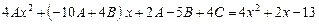Чтобы выполнялось это тождественное равенство, надо, чтобы совпадали коэффициенты при одинаковых степенях x:

.

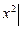
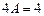
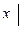
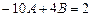
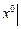
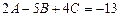Отсюда находим A = 1, B = 3, C = 0. Следовательно,

.

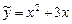Найдем теперь общее решение однородного уравнения:

;

.

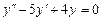
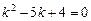
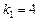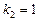
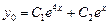Отсюда получаем общее решение исходного уравнения

.

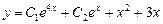II. Пусть в уравнении (1) правая часть имеет вид

,

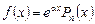где 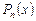– многочлен (в частности, может быть 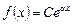, C = const).

В этом случае ищем частное решение 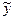по такому правилу:

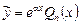, если a – не корень характеристического уравнения,

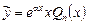, если a – простой корень характеристического уравнения,

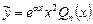, если a – двойной корень характеристического уравнения.

Пример 2. .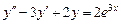

Здесь характеристическое уравнение

, .

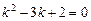
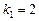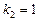Очевидно, a = 3 не является корнем характеристического уравнения. Поэтому 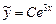, , 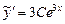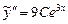. Подставим все это в уравнение:

.

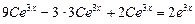Получаем С = 1. Следовательно,

.

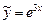Очевидно, общее решение соответствующего однородного уравнения есть

.

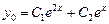Получаем

.

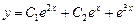III. Пусть теперь 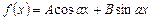(при этом, в частности, может быть А = 0 или В = 0).

В этом случае (если корни характеристического уравнения – действительные) 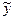ищем в виде

.

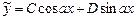Пример 3. .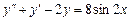

Ищем 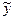в виде 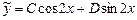. Имеем

,

.

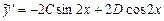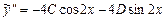Подставляем:

.

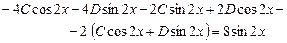
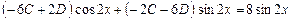Приравниваем коэффициенты пр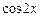и и :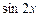

.

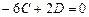
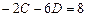Отсюда 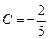, 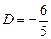. Следовательно,

.

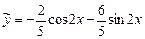Находим :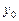

.

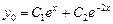Получаем общее решение

.

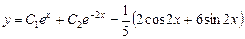Следует обратить внимание на то, что хотя 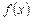содержит только 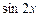и не содержит 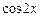, тем не менее 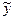содержит 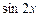и , и .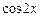

Лекция 9. Ряды

Числовые ряды

Определение 1. Числовым рядом называется бесконечная последовательность чисел 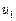, , 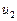..., 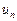, ..., соединенных знаком сложения:

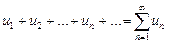. (1)

Числа 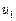, , 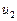..., 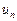, ..., называются членами ряда, а n-й член 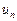– общим членом ряда.

Ряд считается заданным, если известен его общий член 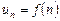. Например, ряд с общим членом 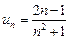имеет вид

,

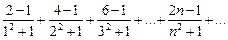или

.

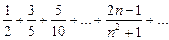Иначе его можно записать в виде .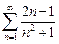

Рассмотрим суммы первых членов ряда (1):

............

............

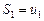
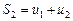
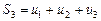
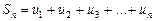
Эти суммы называются частичными суммами ряда (1). Сумма 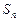называется n-й частичной суммой ряда (1).

Определение 2. Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е.

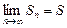. (2)

Этот предел S называется суммой ряда.

Если предел (2) не существует, то ряд называется расходящимся.

Пример. Рассмотрим ряд

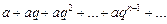. (3)

Это – геометрическая прогрессия (точнее говоря, ряд, составленный из членов геометрической прогрессии).

Из школьного курса известно, что сумма n членов геометрической прогрессии равна

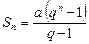
или

.

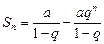Это и есть n-я частичная сумма ряда (3).

Пусть 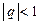. Тогда 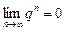, следовательно,

.

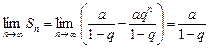Итак, в случае 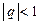ряд (3) сходится и его сумма

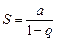
Нетрудно убедиться в том, что при 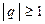ряд (3) расходится.

Свойства сходящихся рядов

1. Если ряд 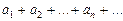сходится и имеет сумму S, то ряд 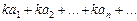(полученный почленным умножением данного ряда на число k) также сходится и имеет сумму kS.

2. Если ряды 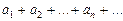и 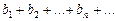сходятся и их суммы соответственно равны 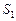и 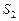, то и ряд 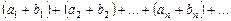также сходится и его сумма равна .

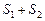3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов.

Если в ряде (1) отбросить первые n членов, то получится ряд

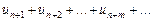, (4)

называемый n-м остатком ряда.

Очевидно, если ряд (1) сходится, то и его остаток (4) также сходится. Если сумму остатка (4) обозначить через 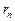, т.е.

,

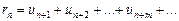то сумму ряда (1) можно представить в виде

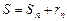. (5)

Отсюда получаем свойство 4.

4. Для того чтобы ряд (1) сходился, необходимо и достаточно, чтобы при 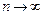остаток ряда стремился к нулю, т.е. .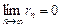