VIII. Решение логарифмических и иррациональных уравнений.
Ошибки, допускаемые учащимися при решении логарифмических уравнений, бывают связаны с неправильным применением формул для логарифмирования произведения, дроби и степени.
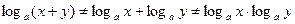 .
.
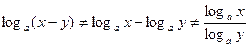 .
.
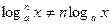 .
.
Используя формулы логарифмирования:
1) 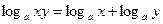 , x > 0, y > 0,
, x > 0, y > 0,
2) 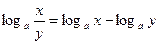 , a
, a 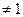 , a > 0
, a > 0
3) 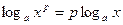 , p – любое действительное число.
, p – любое действительное число.
Нужно помнить, что ОДЗ их левых и правых частей не совпадают. Правые части (1) и (2) имеют смысл, когда x > 0, y > 0.
Левые же части имеют смысл, когда знаки х и у совпадают. Следовательно, при переходе от выражения 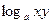 к выражению
к выражению 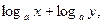 ОДЗ сужается, а это может привести к потере корней.
ОДЗ сужается, а это может привести к потере корней.
Правая часть (3) определена лишь при х > 0, а ОДЗ левой части зависит от показателя степени p. Если р – целое четное число, то левая часть (3) имеет смысл и при отрицательном х. Поэтому переход от выражения 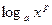 к выражению
к выражению 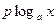 может привести к потере решений уравнения. Поэтому формулы лучше применять в такой форме:
может привести к потере решений уравнения. Поэтому формулы лучше применять в такой форме:
1) 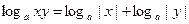 ;
;
2) 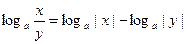 ;
;
3) 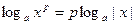 , (р – четное).
, (р – четное).
Используя формулы в таком виде, невозможно потерять корни, можно лишь приобрести посторонние. Но это не так страшно. Просто необходима проверка полученных решений.
Например:
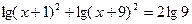 .
.
Неправильное решение:
2lg (x + 1) + 2lg (x + 9) = 2lg9,
lg (x + 1) + lg (x + 9) = lg9,
lg (x + 1) (x +9) = lg9,
(x + 1) (x + 9) = 9,
x  + 10x = 0,
+ 10x = 0,
x 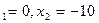 .
.
Правильное решение:
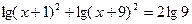 ,
,
ОДЗ: х 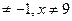 ,
,
2lg |x + 1| + 2lg |x + 9| = 2lg9,
lg |(x + 1) (x + 9)| = lg9,
|x  + 10x + 9| = 0,
+ 10x + 9| = 0,
x 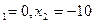 ,
,
a) x  + 10x + 9 = 9 x
+ 10x + 9 = 9 x 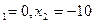 .
.
б) x  + 10x + 9 = -9, x
+ 10x + 9 = -9, x  + 10x + 18 = 0,
+ 10x + 18 = 0,
x 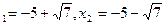 .
.
Это же уравнение можно решить и другим способом:
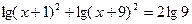 ,
,
ОДЗ: х 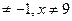 ,
,
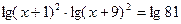 ,
,
((х + 1) (х + 9))  = 81,
= 81,
(x  + 10x + 9)
+ 10x + 9)  = 81,
= 81,
x  + 10x + 9 = 9, x
+ 10x + 9 = 9, x  + 10x + 9 = -9,
+ 10x + 9 = -9,
x 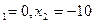 ; x
; x 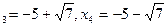 .
.
Пример:
lg x  = 6
= 6
I способ:
2lgx = 6, lgx = 3, x = 1000;
II способ:
На основании определения логарифма, имеем:
x  = 10
= 10 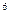 , х =
, х = 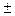 1000.
1000.
Решая первым способом, мы сузили ОДЗ для х, поэтому произошла потеря корня. Правильно применять первый способ нужно так:
lg x  = 6, 2lg|x| = 6, lg|x| = 3, |x| = 1000, x =
= 6, 2lg|x| = 6, lg|x| = 3, |x| = 1000, x = 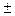 1000.
1000.
Примеры:
1. Решите уравнение: 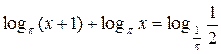
А) 1.
В) 2.
С) -2; 1.
D) 1; 2.
Е) -1; 32.
(Вариант-21 №16 2007г.)
2. Решите уравнение: 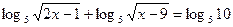 .
.
А) 13.
В) -3,5; 13.
С) -26; 13.
D) -13; 3,5.
Е) 26.
(Вариант-12 №17 2007г.)
3. Решите уравнение: 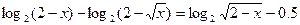
А) 0; 2; 16\9.
В) 16\9; 2.
С) 0; 16\9.
D) 0; 2.
Е) 16\9.
(Вариант-30 №14 2002г.)
4. Решите уравнение: 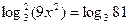
Ответ: 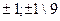 .
.
(№992 2006г. Тестовые задания, Кокшетау)
5. Решите уравнение: 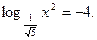
Ответ: 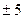 .
.
(№885 2006г. Тестовые задания, Кокшетау)
Коды правильных ответов
| B | A | C | ±1; ±1/9 | ±5 |
Следует иметь в виду для любых уравнений, что при делении, а также умножении уравнения на выражение, содержащее неизвестное, можно потерять или приобрести посторонние корни. Сокращение на выражение, содержащее неизвестное, - это очень распространенная ошибка, которую допускают учащиеся при решении уравнений и неравенств.
Например:
1. Решите уравнение: (х + 4) (х - 7) = х – 7.
Если обе части уравнения разделить на х – 7, то будет потерян корень х= = 7.
Решение:
(х + 4) (х - 7) – (х – 7) = 0, (х – 7) (х + 4 – 1) = 0, х = 7 или х = -3.
Ответ: х = 7, х = -3.
2. Решите уравнение: sin 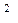 х = sin x.
х = sin x.
sin  х - sin x = 0, sin x (sin x – 1) = 0,
х - sin x = 0, sin x (sin x – 1) = 0,
sin x = 0 или sin x = 1, тогда
x = 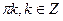 или x =
или x = 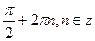 .
.
Eсли же сократить на sin x, то потеряются все корни, для которых sin x = = 0.
Подобных ошибок следует избегать в следующих тестовых заданиях:
1. Решите уравнение: 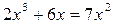
Решение: 2х3 -7х2+6х=0, х(2х2-7х+6)=0, х=0 или 2х2-7х+6=0,
х1=2, х2=1,5
Ответ:0;2;1,5.
А) -2; 0; 1.5.
В) -1.5; 0; 2.
С) 1.5; 2.
D) 0; 1.5; 2.
Е) -1.5; -1; 0.
(Вариант-8 №16 2006г.)
2. Решите уравнение: 2cos x cos 2x – cos x = 0
А) 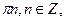
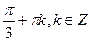 .
.
В) 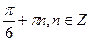 .
.
С) 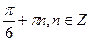 ,
, 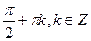 .
.
D) 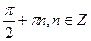 .
.
Е) 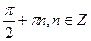 ,
, 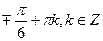
(Вариант-32 №15 2006г.)
3. Решите уравнение: 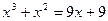 .
.
А) {1; 3; -3}.
В) {-1; 3; -3}.
С) {-1; 3; 1\3}.
D) {1; -3; -1\3}.
Е) {1; -3; 1\3}.
(Вариант-21 №9 2005г.)
4. Решите уравнение: 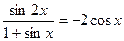 .
.
А) 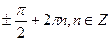 .
.
В) 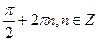 ;
; 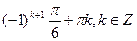 .
.
С) 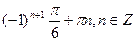 .
.
D) 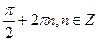 ;
; 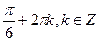 .
.
Е) 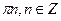 .
.
(Вариант-14 №16 2007г.)
5. Решите уравнение: 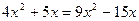 .
.
А) 1\2; 1\3.
В) -3; 1.
С) -9; 0.
D) 0;4.
Е) 2; 6.
(Вариант-25 №7 2005г.)
6. Решите уравнение: sin 2x = sin x.
А) 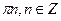 ;
; 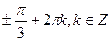 .
.
В) 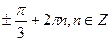 .
.
С) 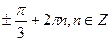 ;
; 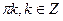 .
.
D) 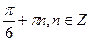 .
.
Е) 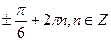 .
.
(Вариант-32 №13 2005г.)
7. Решите уравнение: 1 - cos 2x = 2sin x.
А) 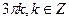 .
.
В) 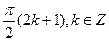 .
.
С) 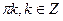 ;
; 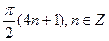 .
.
D) 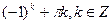 .
.
Е) 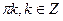 .
.
(Вариант-18 №23 2005г.)
8. Решите уравнение: sin x +sin 2x = cos x +2 cos 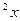 .
.
А) 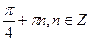 ;
; 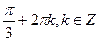 .
.
В) 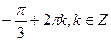 ;
; 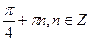 .
.
С) нет корней.
D) 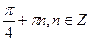 ;
;  .
.
Е) 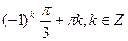 ;
; 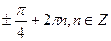 .
.
(Вариант-14 №28 2005г.)
9. Решите уравнение: 2sin  x + 2sin 2x =
x + 2sin 2x = 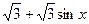 .
.
А) 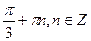 ;
; 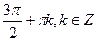 .
.
В) нет решений.
С) 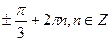 ;
; 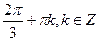 .
.
D) 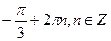 ;
; 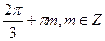 ;
; 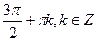 .
.
Е) 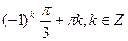 ;
; 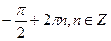 .
.
(Вариант-8 №30 2005г.)
Коды правильных ответов
| D | E | B | B | D | A | C | D | E |
Решения многих уравнений можно упростить введением новой переменной.
Например:
Решите уравнение: 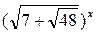 +
+ 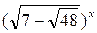 = 14.
= 14.
Пусть 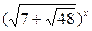 = u,
= u, 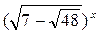 = v.
= v.
Получаем систему: 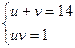 .
.
Решая способом подстановки, находим: 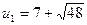 ,
, 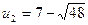 .
.
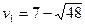 ,
, 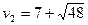 .
.
Возвращаясь к прежней переменной, получаем:
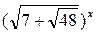 =
= 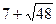 , х = 2.
, х = 2.
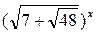 =
= 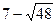 ,
,
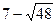 =
= 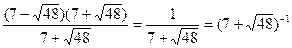 ,
,
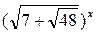 =
= 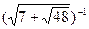 , х = -2.
, х = -2.
Ответ: х 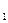 = 2; х
= 2; х 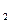 = -2.
= -2.
Использование вспомогательных неизвестных часто существенно ускоряет решение иррациональных уравнений.
Например:
1. 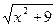 -
- 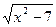 = 2
= 2
Можно ввести две переменные.
Пусть 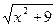 = u,
= u, 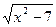 = v.
= v.
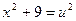 ,
, 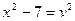 .
.
Получаем систему: 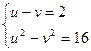 .
. 
Преобразуем второе уравнение: (u – v) (u + v) = 16,
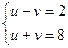 ,
, 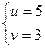 .
.
Возвращаясь к прежней переменной, получим:
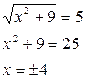
Ответ: х = 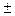 4.
4.
(Вариант-27 №7 2002г.)
(№651 2006г. Тестовые задания, Кокшетау)
2. 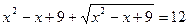
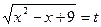 ,
, 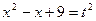 ,
, 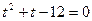 ,
, 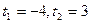 - не является решением.
- не является решением.
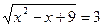 ,
, 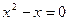 ,
, 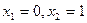 .
.
Ответ: 0; 1.
При решении уравнений такого вида чаще всего применяют способ уединения корня, с последующим возведением обеих частей уравнения в надлежащую степень. И при этом важно иметь в виду, что среди посторонних корней, получающихся при возведении уравнения в степень, могут быть и такие, которые принадлежат ОДЗ, но решением уравнения не являются. Это можно выяснить проверкой.
Например:
Решите уравнение:
4 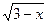 + 6 = 5х, ОДЗ: 3 – х
+ 6 = 5х, ОДЗ: 3 – х 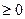 , х
, х 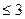 .
.
Уединим корень и возведем обе части в квадрат:
4 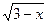 = 5х – 6, 16(3 – х) = 25х
= 5х – 6, 16(3 – х) = 25х  - 60х + 36, 25х
- 60х + 36, 25х  - 44х – 12 = 0.
- 44х – 12 = 0.
Решаем методом «переброски»: 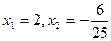 .
.
Оба корня принадлежат ОДЗ, но решением уравнения является только 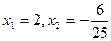 - посторонний корень.
- посторонний корень.
Аналогичные тестовые задания:
1. Решите уравнение: 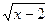 = 8 – х.
= 8 – х.
А) 1.
В) 2.
С) 4.
D) 6.
Е) 3.
(Вариант-14 №7 2002г.)
2. Решите уравнение: 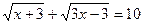
Ответ: 13.
(№669 2006г. Тестовые задания, Кокшетау)
3. Решите уравнение: 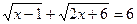
Ответ: 5.
(№648 2006г. Тестовые задания, Кокшетау)
4. Решите уравнение: 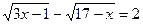
Ответ: 8.
(№646 2006г. Тестовые задания, Кокшетау)
5. Решите уравнение: 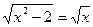
Ответ: 2.
(№643 2006г. Тестовые задания, Кокшетау)
IX. Вычисление производных.
Большое внимание в тестах уделяется вычислению производных. Вычисление производных осуществляется согласно правилам и формулам. Обратим внимание на функции вида:
у = 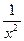 ,
, 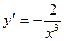 .
.
у = 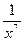 ,
, 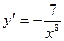 .
.
у = 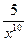 ,
, 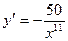 .
.
Сравнивая данную функцию и ее производную, приходим к выводу: чтобы найти производную данной функции, нужно числитель умножить на показатель степени знаменателя с противоположным знаком, а показатель степени увеличить на единицу. Принятие во внимание этого факта поможет сэкономить время при вычислении производных такого вида на ЕНТ:
1. Для функции у = 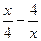 , определите:
, определите:
а) нули;
б) промежутки возрастания;
в) промежутки убывания.
Указание: 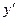 =
= 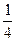 +
+ 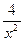
А) а) -4, 4; б) ( 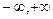 ); в) нет.
); в) нет.
В) а) -4, 4; б) ( 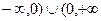 ); в) нет.
); в) нет.
С) а) -4, 0; б) ( 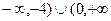 ); в) нет.
); в) нет.
D) а) -4, 4; б) ( 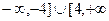 ); в) [-4, 4].
); в) [-4, 4].
Е) а) -4, 0, 4; б) 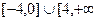 ); в) (
); в) ( 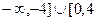 ].
].
(Вариант-1 №24 2002г.)
2. Дана функция f(x) = 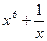 . Найдите
. Найдите 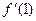 .
.
А) 0.
В) -3.
С) 5.
D) 1.
Е) 6.
(Вариант-31 №11 2007г.)
3. Для функции у = 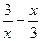 , определите:
, определите:
а) нули;
б) промежутки возрастания;
в) промежутки убывания.
А) а) -3, 3; б)нет; в) ( 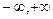 ).
).
В) а) -3, 3; б) ( 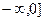 ; в) [0,
; в) [0,  ).
).
С) а) -3, 3; б)нет; в) ( 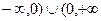 ).
).
D) а) -3, 0, 3; б)[-3, 0], [3,  ); в) (
); в) ( 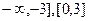 ).
).
Е) а) 3, -3; б) [3, 1], [-3, 0]; в) (0, -3], [0, 3].
(Вариант-11 №29 2003г.)
4. Для функции у = 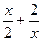 , найдите:
, найдите:
а) все критические точки;
б) точки минимума и точки максимума;
А) а) 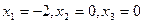 ; б)
; б) 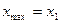 ,
, 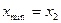 ,
, 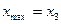 .
.
В) а) 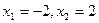 ; б)
; б) 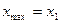 ,
, 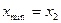 .
.
С) а) 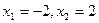 ; б)
; б) 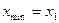 ,
, 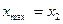
D) а) 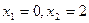 ; б)
; б) 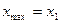 ,
, 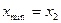 .
.
Е) а) 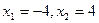 ; б)
; б) 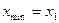 ,
, 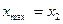
(Вариант-13 №18 2003г.)
Коды правильных ответов
| B | C | C | B |
Очень часто при вычислении производных сложных функций учащиеся допускают ошибки. Находя производную функции y = lg(3x + 5), забывают умножить результат на 3. Почему? Просто многие из них не владеют понятием сложной функции. Поэтому при вычислении производных необходима последовательность рассуждений:
1. Определить вид функции (линейная, квадратичная, логарифмическая, степенная и т.д.)
2. Если – да, то ее производная берется согласно известным формулам.
3. Если – нет, то можно ли данную функцию представить в виде суммы (разности), произведения или частного указанных функций.
4. Если – да, то работаем с соответствующими формулами.
5. Если – нет, то надо рассматривать данную функцию как сложную.
Например:
Найти производную функции у = (2х – 4) 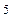 .
.
Последовательно рассуждая, приходим к выводу, что данная функция сложная: степенная от линейной. Значит, ее производная равна произведению производной степенной и линейной функций 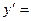 10(2х – 4).
10(2х – 4).
Аналогичные примеры можно найти в следующих тестовых заданиях:
1. Дана функция f(x) = 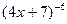 . Найдите
. Найдите 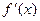 .
.
Решение: 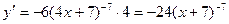
А) -42(4х + 7) 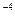 .
.
В) -6(4х + 7) 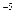 .
.
С) -4(4х + 7) 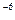 .
.
D) -24(4х + 7) 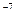 .
.
Е) -4(4х + 7) 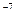 .
.
(Вариант-11 №10 2006г.)
2. Найдите производную функции у = (1/3 х – 6) 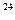 .
.
А) 8(1/3х – 6) 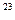 .
.
В) 6(1/3х – 6) 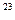 .
.
С) 24(1/3х – 6) 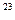 .
.
D) 1/3(1/3х – 6) 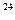 .
.
Е) 72(1/3х – 6) 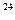 .
.
(Вариант-12 №9 2006г.)
3. Дано f(x) = 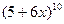 . Найдите
. Найдите 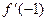 .
.
А) -10.
В) 10.
С) -60.
D) 6.
Е) 60.
(Вариант-13 №10 2006г.)
4. Найдите производную функции: f(x) = 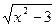 .
.
А) 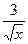 .
.
В) 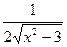 .
.
С) 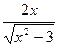 .
.
D) 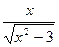 .
.
Е) 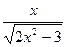 .
.
(Вариант-16 №9 2006г.)
5. Найдите производную функции: f(x) = (2x – 6)  .
.
А) -7(2x – 6) 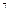 .
.
В) 16(2x – 6) 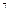 .
.
С) -7(2x + 6) 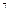 .
.
D) 4(2x – 6) 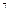 .
.
Е) 8(2x – 6) 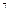 .
.
(Вариант-16 №10 2006г.)
6. Дана функция 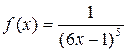 , найдите
, найдите 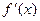
А) 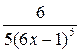 .
.
В) 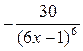 .
.
С) 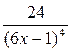 .
.
D) 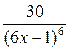 .
.
Е) 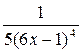 .
.
(Вариант-3 №23 2002г.)
7. Найдите производную функции: f(x) = 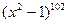 .
.
А) 102x( 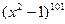 .
.
В) 204 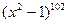 .
.
С) 102 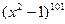 .
.
D) 2x 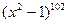 .
.
Е) 204 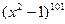 .
.
(Вариант-7 №24 2002г.)
8. Найдите производную функции: f(x) = 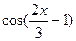 .
.
А) 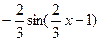 .
.
В) 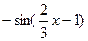 .
.
С) 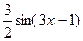 .
.
D) 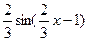 .
.
Е) 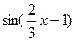 .
.
(Вариант-6 №21 2003г.)
9. Найдите производную функции: y = 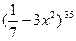 .
.
А) 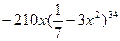 .
.
В) 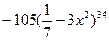 .
.
С) 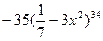 .
.
D) 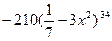 .
.
Е) 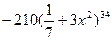 .
.
(Вариант-8 №19 2003г.)
Коды правильных ответов
| D | A | C | D | B | B | E | A | A |
