Возведение в квадрат двузначных чисел, оканчивающихся на 5.
I. Вычисляем быстро.
1. Умножение двузначных чисел (метод Ферроля).
Этот способ следует из тождества:
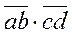 =(10a+b) (10c+d) = 100ac + 10bc + 10ad + bd= 100ac +10(bc+ad) + bd
=(10a+b) (10c+d) = 100ac + 10bc + 10ad + bd= 100ac +10(bc+ad) + bd
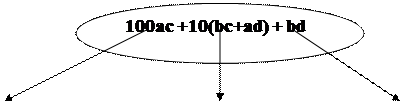 |



Получается алгоритм, который продемонстрируем на примере:
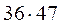
а) 6 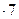 = 42; два пишем и 4 запоминаем;
= 42; два пишем и 4 запоминаем;
б) 6 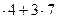 = 24 + 21 = 45, да ещё запоминали 4: 45 + 4 = 49; девять пишем и четыре запоминаем;
= 24 + 21 = 45, да ещё запоминали 4: 45 + 4 = 49; девять пишем и четыре запоминаем;
в) 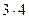 = 12, да ещё запоминали 4: 12 + 4 = 16.
= 12, да ещё запоминали 4: 12 + 4 = 16.
Таким образом, получаем 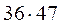 = 1692.
= 1692.
· Методом Ферроля легко перемножать устно двузначные числа от 10 до 20.
Например, чтобы умножить 13 на 12, делаем так:
а) 3 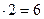 (единицы),
(единицы),
б) 3 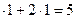 (десятки),
(десятки),
в) 1 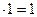 (сотни).
(сотни).
Получаем: 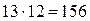 .
.
· Можно умножать и трехзначное число на двухзначное число.
Например: 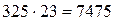
а) 5 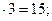 пишем пять, один запоминаем.
пишем пять, один запоминаем.
б) 3 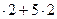 = 16; 16 + 1 = 17; пишем семь, один запоминаем.
= 16; 16 + 1 = 17; пишем семь, один запоминаем.
в) 3 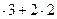 = 13; 13 + 1 =14; пишем четыре, один запоминаем.
= 13; 13 + 1 =14; пишем четыре, один запоминаем.
г) 3 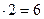 ; 6 + 1 = 7.
; 6 + 1 = 7.
2. Рациональный метод возведения в квадрат двузначного числа.
Этот метод основывается на следующих рассуждениях:
( 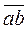 )
) 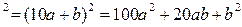 =100
=100 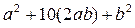
Например:
1) 53  =2809.
=2809.
а) 3 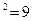 ,
,
б) (5 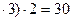 ; ноль пишем, три запоминаем;
; ноль пишем, три запоминаем;
в) 5 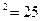 ; 25 + 3 = 28.
; 25 + 3 = 28.
2) 64 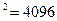 .
.
а) 4 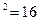 ; шесть пишем, один запоминаем;
; шесть пишем, один запоминаем;
б) (6 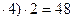 ; 48 + 1 = 49; девять пишем, четыре запоминаем;
; 48 + 1 = 49; девять пишем, четыре запоминаем;
в) 6 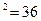 ; 36 + 4 = 40.
; 36 + 4 = 40.
Возведение в квадрат двузначных чисел, оканчивающихся на 5.
(10a + 5) 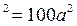 + 100a + 25 = 100a (a+1) + 25,
+ 100a + 25 = 100a (a+1) + 25,
где a – цифра десятков, 25 – две последние цифры полученного числа:
95  = 9025 (9
= 9025 (9 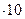 = 90 и приписываем 25), т.е.
= 90 и приписываем 25), т.е.
Для возведения в квадрат числа, запись которого оканчивается цифрой 5, необходимо число десятков умножить на число, увеличенное на единицу, к полученному произведению приписать справа 25.
Этот метод можно использовать для возведения в квадрат трёхзначных чисел, оканчивающихся на 5.
Например:
405  = 164025 (40
= 164025 (40 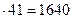 и приписываем 25);
и приписываем 25);
165 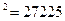 (16
(16 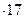 - можно применить метод Ферроля).
- можно применить метод Ферроля).
Все эти правила можно применять при возведении в квадрат десятичных дробей.
4. Применение формулы произведения суммы двух чисел на их разность 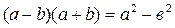 :
:
78 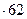 = (70+8) (70-8) = 4900 – 64 = 4836;
= (70+8) (70-8) = 4900 – 64 = 4836;
8,3 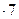 ,7 = (8+0,3) (8-0,3) = 64 – 0,09 = 63,91.
,7 = (8+0,3) (8-0,3) = 64 – 0,09 = 63,91.
5. Применение формулы 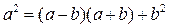
Пример 1:
Возведём в квадрат 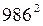 :
:
Заметим, что 986 + 14 = 1000. Пусть тогда a = 986, b = 14.
a + b = 1000, a – b = 972. Применяя формулу, получаем:
986  = 1000
= 1000 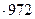 +196 = 972196.
+196 = 972196.
Пример 2:
Вычислим 488 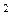 :
:
488 + 12 = 500; a = 488, b = 12; a + b = 500, a – b =476.
488  = 500
= 500 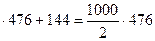 +144 = 238000 + 144 = 238144.
+144 = 238000 + 144 = 238144.
Умножение чисел, у которых число десятков одинаковое, а сумма единиц равна 10.
Этот способ основан на тождестве: (10a + b) (10a + c) = 100a (a +1) + bc, где b + c =10
Например:
1) 12 · 18 = 216
· число десятков умножаем на число, которое больше на единицу, 1· 2 = 2;
· перемножаем единицы этих чисел и справа дописываем к первому результату 8 · 2 = 16.
2) 46 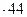 = 2024
= 2024
· 4 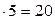 ;
;
· 6 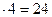 .
.
3) 317 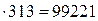
· 31 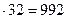 (можно применить метод Ферроля);
(можно применить метод Ферроля);
· 7 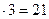 .
.
Умножение чисел на 11.
Записать последнюю цифру числа, затем последовательно, справа налево записывать суммы соседних двух цифр множимого и, наконец, первую цифру множимого.
Например:
1. 43 · 11 = 473
· пишем 3;
· 4 + 3 = 7, пишем 7;
· пишем 4.
2. 135 · 11= 1485.
· пишем 5;
· 3 + 5 = 8;
· пишем 14.
Если одна из сумм соседних цифр окажется больше 9, то в этом разряде записывают цифру единиц полученной суммы, а в следующем прибавляют 1.
Например:
1. 57 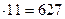
1) пишем 7,
2) 5 + 7 = 12, пишем 2 и запоминаем 1,
3) 5 + 1 = 6.
2. 389 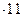 = 4279
= 4279
1) пишем 9,
2) 8 + 9 = 17, пишем 7 и запоминаем 1,
3) 3 + 8 = 11, 11 + 1 = 12, пишем 2, запоминаем 1,
4) 3 + 1 = 4.
8. Умножение на числа вида 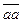 : умножить данное число на a, потом на 11.
: умножить данное число на a, потом на 11.
Например:
235 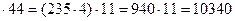
Умножение двузначных чисел на 111
Справа налево нужно последовательно записать последнюю цифру первого множителя, сумму цифр первого множителя, снова сумму его цифр и, наконец, первую цифру. Если сумма цифр двузначного числа больше 9, то записываем цифру единиц каждой суммы, а к следующему разряду прибавляем 1.
Например:
36 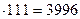 ;
;
58 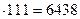 .
.
Умножение на 5, 50.
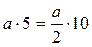 ;
; 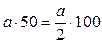 .
.
Умножение на 25, 250.
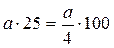 ,
, 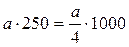 .
.
Деление на 5 и 50.
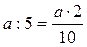 ;
; 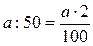 .
.
Деление на 25 и 250.
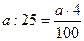 ;
; 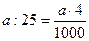 .
.
Умножение на 9,99, 999 и т.д.
В этом случае умножение сводится к умножению на 10, 100, 1000 и т.д. и вычитанию из полученного произведения первого множителя.
Например:
68 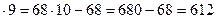 ;
;
85 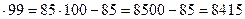 ;
;
85 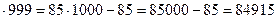 .
.
Сложение столбцами.
Сумма цифр каждого разряда складывается отдельно. Цифра десятков в сумме предыдущего разряда складывается с цифрой единиц последующей суммы.
Например:
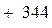 129 129  15 14 . 15 14 . | 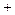 97246 46527 97246 46527 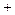 11 13 . 11 13 . |
III. Метод Крамера.
Системы линейных уравнений с двумя неизвестными можно решать методом подстановки, методом сложения, а можно применять метод Крамера или метод определителей. Учащимся, интересующимся математикой, этот метод нравится, и они его используют при подготовке к ЕНТ.
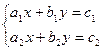
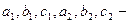 некоторые числа
некоторые числа
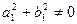 ,
, 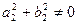
По коэффициентам системы составляются три определителя:
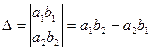
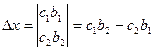
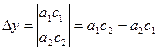
1) Если 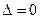 , а
, а 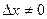 или
или 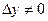 , то система не имеет решений.
, то система не имеет решений.
2) Если 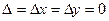 , то система имеет бесконечное множество решений.
, то система имеет бесконечное множество решений.
3) Если 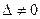 , то система имеет единственное решение:
, то система имеет единственное решение: 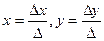 .
.
Например:
Решите систему уравнений 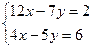
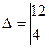
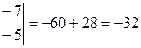
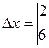
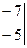 = -10 + 42 = 32
= -10 + 42 = 32
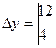
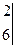 = 72 - 8 = 64
= 72 - 8 = 64
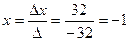 , у =
, у = 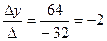
Ответ: (-1; -2).
Этим методом можно решить системы:
1. Решите систему уравнений: 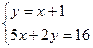
А) (-1; 0).
В) (2; 3).
С) (-2; -1).
D) (6; 7).
Е) (4; 5).
(Вариант-19 №5 2003г.)
2. Решите систему уравнений: 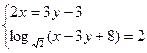
Указание к решению: от данной системы переходим к системе 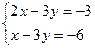 .
.
А) (3; 3).
В) (7; 8).
С) (-3; -1).
D) (-3; -3).
Е) (-1; 3).
(Вариант-26 №24 2003г.)
3. Решите систему уравнений: 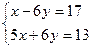
А) (-13; -5).
В) (-1; -3).
С) (-7; -4).
D) (5; -2).
Е) (11; -1).
(Вариант-19, №15, 2004г.)
4. Решите систему уравнений: 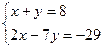
А) (-3; 5).
В) (5; 3).
С) (-5; -3).
D) (3; 5).
Е) (3; -5).
(Вариант-24, №15, 2004г.)
5. Решите систему уравнений: 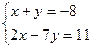
А) (-5; -3).
В) (-3; 5).
С) (5; 3).
D) (3; 5).
Е) (3; -5).
(Вариант-2, №6, 2005г.)
6. Решите систему уравнений: 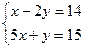
А) (2; -7).
В) (7; 2).
С) (5; 0).
D) (0; 4).
Е) (4; -5).
(Вариант-26, №6, 2005г.)
7. Решите систему уравнений: 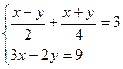
А) (1; 7).
В) (-6; 0).
С) (5; 3).
D) (0; 6).
Е) (-5; 3).
(Вариант-23, №19, 2007г.)
8. Решите систему уравнений: 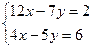
А) (2; 4).
В) (1\6; 0).
С) (-2; -1).
D) (4; 2).
Е) (-1; -2).
(Вариант-15, №14, 2004г.)
Коды правильных ответов
| B | A | D | D | A | E | C | E |
Увидел степень – понижай.
Например:
Решите уравнение: 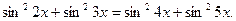
Решение: увидел степень – понижай
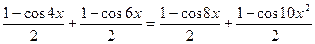 ,
,
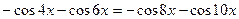 ,
,
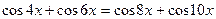 ,
,
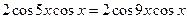 ,
, 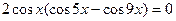 , тогда а)
, тогда а) 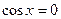 ,
, 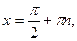
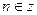 ; в)
; в) 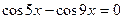 , преобразуем в произведение
, преобразуем в произведение 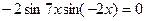 .
. 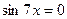 ,
, 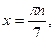
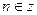 .
.
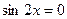 ,
, 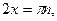
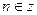 ,
, 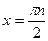 ,
, 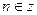 .
.
А) 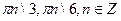 .
.
В) 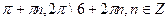 .
.
С) 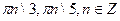 .
.
D) 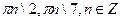 .
.
Е) 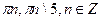 .
.
(Вариант-29 №22 2002г.)
1. Решите уравнение: sin 2x sin 4x = cos 2x.
А) 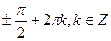 .
.
В) 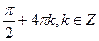 .
.
С) 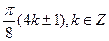 .
.
D) 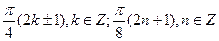 .
.
Е) 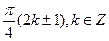 .
.
(Вариант-29 №21 2002г.)
2. Решите уравнение: sin 5x + sin x = 2 sin 3x.
А) 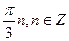 .
.
В) 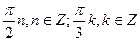 .
.
С) 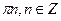 .
.
D) 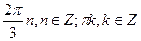 .
.
Е) 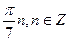 .
.
(Вариант-28 №21 2002г.)
3. Решите уравнение: cos 5x cos x = cos 4x.
А) 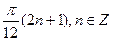 .
.
В) 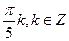 .
.
С) 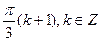 .
.
D) 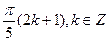 .
.
Е) 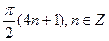 .
.
(Вариант-9 №15 2006г.)
4. Решите уравнение: sin x sin 2x +cos 3x = 0.
А) 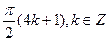 .
.
В) 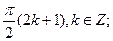
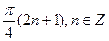 .
.
С) 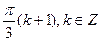 .
.
D) 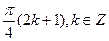 .
.
Е) 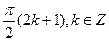 .
.
(Вариант-26 №15 2006г.)
5. Решите уравнение: sin 2x cos 3x = sin 5x.
А) 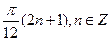 .
.
В) 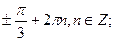
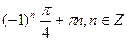 .
.
С) 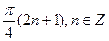 .
.
D) 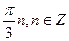 ;
; 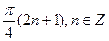 .
.
Е) 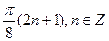 .
.
(Вариант-29 №16 2007г.)
6. Решите уравнение: sin 5x sin 4x + cos 6x cos 3x = 0.
А) 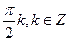 .
.
В) 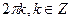 .
.
С) 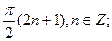
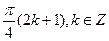 .
.
D) 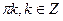 .
.
Е) 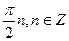 ;
; 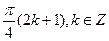 .
.
(Вариант-29 №4 2004г.)
Коды правильных ответов
| D | D | E | B | B | D | C |
Следует иметь в виду для любых уравнений, что при делении, а также умножении уравнения на выражение, содержащее неизвестное, можно потерять или приобрести посторонние корни. Сокращение на выражение, содержащее неизвестное, - это очень распространенная ошибка, которую допускают учащиеся при решении уравнений и неравенств.
Например:
1. Решите уравнение: (х + 4) (х - 7) = х – 7.
Если обе части уравнения разделить на х – 7, то будет потерян корень х= = 7.
Решение:
(х + 4) (х - 7) – (х – 7) = 0, (х – 7) (х + 4 – 1) = 0, х = 7 или х = -3.
Ответ: х = 7, х = -3.
2. Решите уравнение: sin 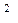 х = sin x.
х = sin x.
sin  х - sin x = 0, sin x (sin x – 1) = 0,
х - sin x = 0, sin x (sin x – 1) = 0,
sin x = 0 или sin x = 1, тогда
x = 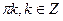 или x =
или x = 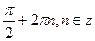 .
.
Eсли же сократить на sin x, то потеряются все корни, для которых sin x = = 0.
Подобных ошибок следует избегать в следующих тестовых заданиях:
1. Решите уравнение: 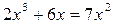
Решение: 2х3 -7х2+6х=0, х(2х2-7х+6)=0, х=0 или 2х2-7х+6=0,
х1=2, х2=1,5
Ответ:0;2;1,5.
А) -2; 0; 1.5.
В) -1.5; 0; 2.
С) 1.5; 2.
D) 0; 1.5; 2.
Е) -1.5; -1; 0.
(Вариант-8 №16 2006г.)
2. Решите уравнение: 2cos x cos 2x – cos x = 0
А) 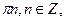
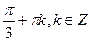 .
.
В) 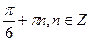 .
.
С) 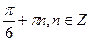 ,
, 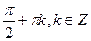 .
.
D) 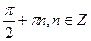 .
.
Е) 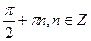 ,
, 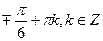
(Вариант-32 №15 2006г.)
3. Решите уравнение: 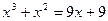 .
.
А) {1; 3; -3}.
В) {-1; 3; -3}.
С) {-1; 3; 1\3}.
D) {1; -3; -1\3}.
Е) {1; -3; 1\3}.
(Вариант-21 №9 2005г.)
4. Решите уравнение: 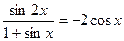 .
.
А) 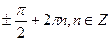 .
.
В) 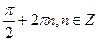 ;
; 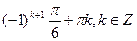 .
.
С) 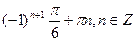 .
.
D) 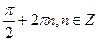 ;
; 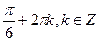 .
.
Е) 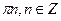 .
.
(Вариант-14 №16 2007г.)
5. Решите уравнение: 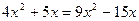 .
.
А) 1\2; 1\3.
В) -3; 1.
С) -9; 0.
D) 0;4.
Е) 2; 6.
(Вариант-25 №7 2005г.)
6. Решите уравнение: sin 2x = sin x.
А) 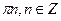 ;
; 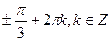 .
.
В) 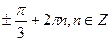 .
.
С) 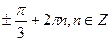 ;
; 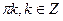 .
.
D) 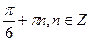 .
.
Е) 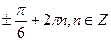 .
.
(Вариант-32 №13 2005г.)
7. Решите уравнение: 1 - cos 2x = 2sin x.
А) 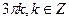 .
.
В) 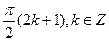 .
.
С) 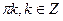 ;
; 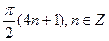 .
.
D) 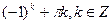 .
.
Е) 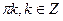 .
.
(Вариант-18 №23 2005г.)
8. Решите уравнение: sin x +sin 2x = cos x +2 cos 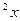 .
.
А) 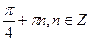 ;
; 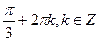 .
.
В) 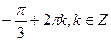 ;
; 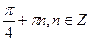 .
.
С) нет корней.
D) 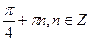 ;
;  .
.
Е) 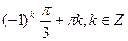 ;
; 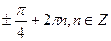 .
.
(Вариант-14 №28 2005г.)
9. Решите уравнение: 2sin  x + 2sin 2x =
x + 2sin 2x = 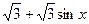 .
.
А) 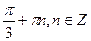 ;
; 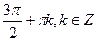 .
.
В) нет решений.
С) 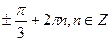 ;
; 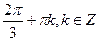 .
.
D) 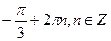 ;
; 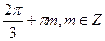 ;
; 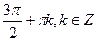 .
.
Е) 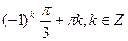 ;
; 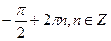 .
.
(Вариант-8 №30 2005г.)
Коды правильных ответов
| D | E | B | B | D | A | C | D | E |
Решения многих уравнений можно упростить введением новой переменной.
Например:
Решите уравнение: 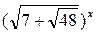 +
+ 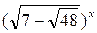 = 14.
= 14.
Пусть 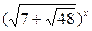 = u,
= u, 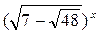 = v.
= v.
Получаем систему: 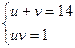 .
.
Решая способом подстановки, находим: 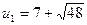 ,
, 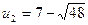 .
.
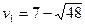 ,
, 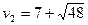 .
.
Возвращаясь к прежней переменной, получаем:
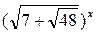 =
= 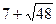 , х = 2.
, х = 2.
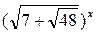 =
= 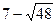 ,
,
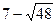 =
= 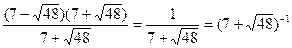 ,
,
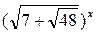 =
= 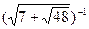 , х = -2.
, х = -2.
Ответ: х 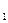 = 2; х
= 2; х 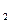 = -2.
= -2.
Использование вспомогательных неизвестных часто существенно ускоряет решение иррациональных уравнений.
Например:
1. 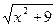 -
- 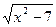 = 2
= 2
Можно ввести две переменные.
Пусть 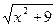 = u,
= u, 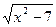 = v.
= v.
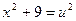 ,
, 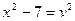 .
.
Получаем систему: 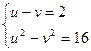 .
. 
Преобразуем второе уравнение: (u – v) (u + v) = 16,
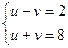 ,
, 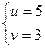 .
.
Возвращаясь к прежней переменной, получим:
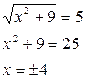
Ответ: х = 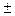 4.
4.
(Вариант-27 №7 2002г.)
(№651 2006г. Тестовые задания, Кокшетау)
2. 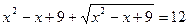
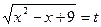 ,
, 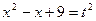 ,
, 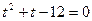 ,
, 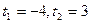 - не является решением.
- не является решением.
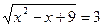 ,
, 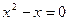 ,
, 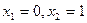 .
.
Ответ: 0; 1.
При решении уравнений такого вида чаще всего применяют способ уединения корня, с последующим возведением обеих частей уравнения в надлежащую степень. И при этом важно иметь в виду, что среди посторонних корней, получающихся при возведении уравнения в степень, могут быть и такие, которые принадлежат ОДЗ, но решением уравнения не являются. Это можно выяснить проверкой.
Например:
Решите уравнение:
4 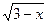 + 6 = 5х, ОДЗ: 3 – х
+ 6 = 5х, ОДЗ: 3 – х 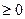 , х
, х 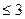 .
.
Уединим корень и возведем обе части в квадрат:
4 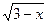 = 5х – 6, 16(3 – х) = 25х
= 5х – 6, 16(3 – х) = 25х  - 60х + 36, 25х
- 60х + 36, 25х  - 44х – 12 = 0.
- 44х – 12 = 0.
Решаем методом «переброски»: 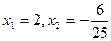 .
.
Оба корня принадлежат ОДЗ, но решением уравнения является только 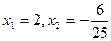 - посторонний корень.
- посторонний корень.
Аналогичные тестовые задания:
1. Решите уравнение: 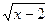 = 8 – х.
= 8 – х.
А) 1.
В) 2.
С) 4.
D) 6.
Е) 3.
(Вариант-14 №7 2002г.)
2. Решите уравнение: 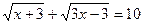
Ответ: 13.
(№669 2006г. Тестовые задания, Кокшетау)
3. Решите уравнение: 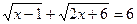
Ответ: 5.
(№648 2006г. Тестовые задания, Кокшетау)
4. Решите уравнение: 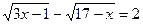
Ответ: 8.
(№646 2006г. Тестовые задания, Кокшетау)
5. Решите уравнение: 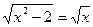
Ответ: 2.
(№643 2006г. Тестовые задания, Кокшетау)
IX. Вычисление производных.
Большое внимание в тестах уделяется вычислению производных. Вычисление производных осуществляется согласно правилам и формулам. Обратим внимание на функции вида:
у = 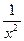 ,
, 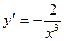 .
.
у = 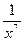 ,
, 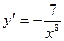 .
.
у = 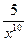 ,
, 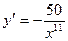 .
.
Сравнивая данную функцию и ее производную, приходим к выводу: чтобы найти производную данной функции, нужно числитель умножить на показатель степени знаменателя с противоположным знаком, а показатель степени увеличить на единицу. Принятие во внимание этого факта поможет сэкономить время при вычислении производных такого вида на ЕНТ:
1. Для функции у = 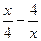 , определите:
, определите:
а) нули;
б) промежутки возрастания;
в) промежутки убывания.
Указание: 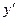 =
= 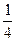 +
+ 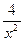
А) а) -4, 4; б) ( 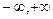 ); в) нет.
); в) нет.
В) а) -4, 4; б) ( 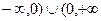 ); в) нет.
); в) нет.
С) а) -4, 0; б) ( 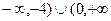 ); в) нет.
); в) нет.
D) а) -4, 4; б) ( 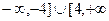 ); в) [-4, 4].
); в) [-4, 4].
Е) а) -4, 0, 4; б) 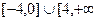 ); в) (
); в) ( 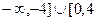 ].
].
(Вариант-1 №24 2002г.)
2. Дана функция f(x) = 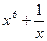 . Найдите
. Найдите 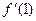 .
.
А) 0.
В) -3.
С) 5.
D) 1.
Е) 6.
(Вариант-31 №11 2007г.)
3. Для функции у = 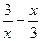 , определите:
, определите:
а) нули;
б) промежутки возрастания;
в) промежутки убывания.
А) а) -3, 3; б)нет; в) ( 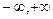 ).
).
В) а) -3, 3; б) ( 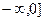 ; в) [0,
; в) [0,  ).
).
С) а) -3, 3; б)нет; в) ( 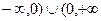 ).
).
D) а) -3, 0, 3; б)[-3, 0], [3,  ); в) (
); в) ( 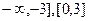 ).
).
Е) а) 3, -3; б) [3, 1], [-3, 0]; в) (0, -3], [0, 3].
(Вариант-11 №29 2003г.)
4. Для функции у = 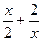 , найдите:
, найдите:
а) все критические точки;
б) точки минимума и точки максимума;
А) а) 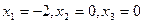 ; б)
; б) 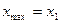 ,
, 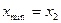 ,
, 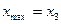 .
.
В) а) 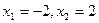 ; б)
; б) 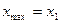 ,
, 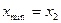 .
.
С) а) 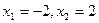 ; б)
; б) 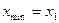 ,
, 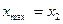
D) а) 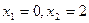 ; б)
; б) 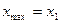 ,
, 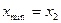 .
.
Е) а) 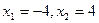 ; б)
; б) 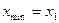 ,
, 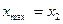
(Вариант-13 №18 2003г.)
Коды правильных ответов
| B | C | C | B |
Очень часто при вычислении производных сложных функций учащиеся допускают ошибки. Находя производную функции y = lg(3x + 5), забывают умножить результат на 3. Почему? Просто многие из них не владеют понятием сложной функции. Поэтому при вычислении производных необходима последовательность рассуждений:
1. Определить вид функции (линейная, квадратичная, логарифмическая, степенная и т.д.)
2. Если – да, то ее производная берется согласно известным формулам.
3. Если – нет, то можно ли данную функцию представить в виде суммы (разности), произведения или частного указанных функций.
4. Если – да, то работаем с соответствующими формулами.
5. Если – нет, то надо рассматривать данную функцию как сложную.
Например:
Найти производную функции у = (2х – 4) 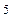 .
.
Последовательно рассуждая, приходим к выводу, что данная функция сложная: степенная от линейной. Значит, ее производная равна произведению производной степенной и линейной функций 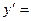 10(2х – 4).
10(2х – 4).
Аналогичные примеры можно найти в следующих тестовых заданиях:
1. Дана функция f(x) = 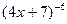 . Найдите
. Найдите 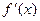 .
.
Решение: 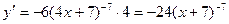
А) -42(4х + 7) 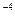 .
.
В) -6(4х + 7) 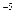 .
.
С) -4(4х + 7) 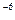 .
.
D) -24(4х + 7) 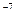 .
.
Е) -4(4х + 7) 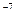 .
.
(Вариант-11 №10 2006г.)
2. Найдите производную функции у = (1/3 х – 6) 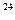 .
.
А) 8(1/3х – 6) 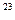 .
.
В) 6(1/3х – 6) 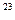 .
.
С) 24(1/3х – 6) 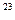 .
.
D) 1/3(1/3х – 6) 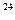 .
.
Е) 72(1/3х – 6) 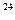 .
.
(Вариант-12 №9 2006г.)
3. Дано f(x) = 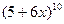 . Найдите
. Найдите 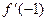 .
.
А) -10.
В) 10.
С) -60.
D) 6.
Е) 60.
(Вариант-13 №10 2006г.)
4. Найдите производную функции: f(x) = 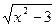 .
.
А) 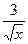 .
.
В) 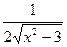 .
.
С) 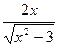 .
.
D) 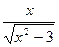 .
.
Е) 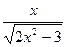 .
.
(Вариант-16 №9 2006г.)
5. Найдите производную функции: f(x) = (2x – 6)  .
.
А) -7(2x – 6) 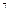 .
.
В) 16(2x – 6) 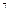 .
.
С) -7(2x + 6) 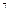 .
.
D) 4(2x – 6) 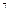 .
.
Е) 8(2x – 6) 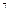 .
.
(Вариант-16 №10 2006г.)
6. Дана функция 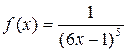 , найдите
, найдите 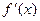
А) 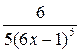 .
.
В) 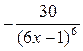 .
.
С) 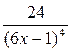 .
.
D) 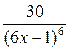 .
.
Е) 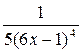 .
.
(Вариант-3 №23 2002г.)
7. Найдите производную функции: f(x) = 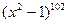 .
.
А) 102x( 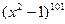 .
.
В) 204 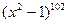 .
.
С) 102 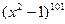 .
.
D) 2x 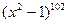 .
.
Е) 204 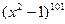 .
.
(Вариант-7 №24 2002г.)
8. Найдите производную функции: f(x) = 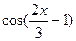 .
.
А) 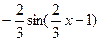 .
.
В) 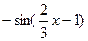 .
.
С) 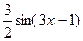 .
.
D) 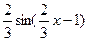 .
.
Е) 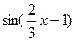 .
.
(Вариант-6 №21 2003г.)
9. Найдите производную функции: y = 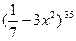 .
.
А) 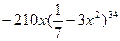 .
.
В) 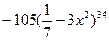 .
.
С) 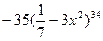 .
.
D) 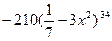 .
.
Е) 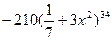 .
.
(Вариант-8 №19 2003г.)
Коды правильных ответов
| D | A | C | D | B | B | E | A | A |
I. Вычисляем быстро.
1. Умножение двузначных чисел (метод Ферроля).
Этот способ следует из тождества:
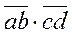 =(10a+b) (10c+d) = 100ac + 10bc + 10ad + bd= 100ac +10(bc+ad) + bd
=(10a+b) (10c+d) = 100ac + 10bc + 10ad + bd= 100ac +10(bc+ad) + bd
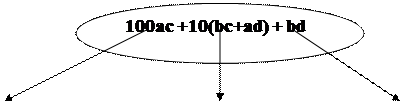 |



Получается алгоритм, который продемонстрируем на примере:
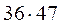
а) 6 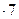 = 42; два пишем и 4 запоминаем;
= 42; два пишем и 4 запоминаем;
б) 6 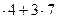 = 24 + 21 = 45, да ещё запоминали 4: 45 + 4 = 49; девять пишем и четыре запоминаем;
= 24 + 21 = 45, да ещё запоминали 4: 45 + 4 = 49; девять пишем и четыре запоминаем;
в) 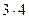 = 12, да ещё запоминали 4: 12 + 4 = 16.
= 12, да ещё запоминали 4: 12 + 4 = 16.
Таким образом, получаем 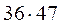 = 1692.
= 1692.
· Методом Ферроля легко перемножать устно двузначные числа от 10 до 20.
Например, чтобы умножить 13 на 12, делаем так:
а) 3 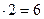 (единицы),
(единицы),
б) 3 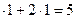 (десятки),
(десятки),
в) 1 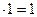 (сотни).
(сотни).
Получаем: 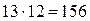 .
.
· Можно умножать и трехзначное число на двухзначное число.
Например: 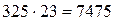
а) 5 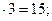 пишем пять, один запоминаем.
пишем пять, один запоминаем.
б) 3 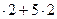 = 16; 16 + 1 = 17; пишем семь, один запоминаем.
= 16; 16 + 1 = 17; пишем семь, один запоминаем.
в) 3 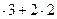 = 13; 13 + 1 =14; пишем четыре, один запоминаем.
= 13; 13 + 1 =14; пишем четыре, один запоминаем.
г) 3 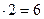 ; 6 + 1 = 7.
; 6 + 1 = 7.
2. Рациональный метод возведения в квадрат двузначного числа.
Этот метод основывается на следующих рассуждениях:
( 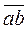 )
) 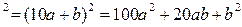 =100
=100 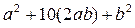
Например:
1) 53  =2809.
=2809.
а) 3 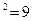 ,
,
б) (5 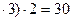 ; ноль пишем, три запоминаем;
; ноль пишем, три запоминаем;
в) 5 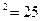 ; 25 + 3 = 28.
; 25 + 3 = 28.
2) 64 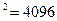 .
.
а) 4
