Первообразная и неопределенный интеграл

Определение 1. Функция 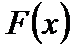называется первообразной для функции 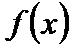, если

.

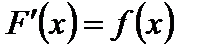Например, 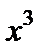есть первообразная для 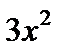, так как 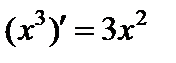; 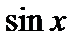есть первообразная для 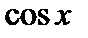, так как .

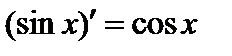Очевидно, если для данной функции 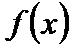существует первообразная, то эта первообразная не является единственной. Так, в предыдущем примере можно было взять в качестве первообразной для 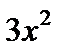не только 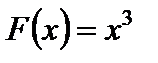, но и 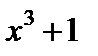, 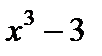или вообще 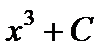(где С – любое, С = const), так как .

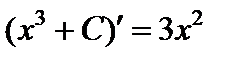Можно доказать, что если 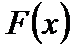есть первообразная для 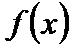, то всякая первообразная для 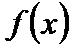имеет вид 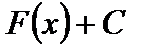, где С = const.

Определение 2. Если функция 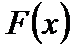является первообразной для 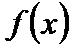, то выражение 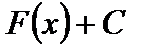называется неопределенным интегралом от функции 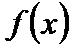и обозначается

.

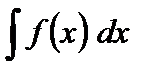Итак, если

,

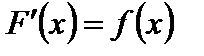то

.

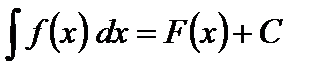При этом 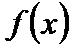называется подынтегральной функцией, а выражение 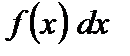– подынтегральным выражением.

Из определения ясно, что неопределенный интеграл представляет собой семейство функцией .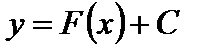

Нетрудно убедиться, в частности, что справедливы равенства:

, ,

.

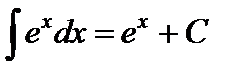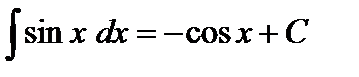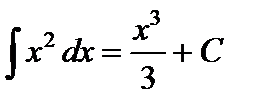Из определения 2 непосредственно получаем следующие свойства:

1. Производная от неопределенного интеграла равна подынтегральной функции, т.е.

.

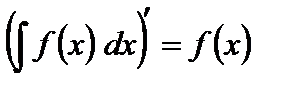2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:

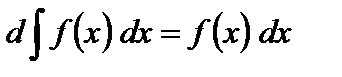
(т.е. знаки d и ò в указанном порядке взаимно уничтожаются).

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная

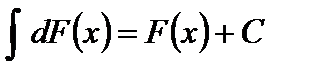
(т.е. знаки òи d, когда d стоит после ò также взаимно уничтожаются, но при этом к 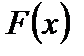надо прибавить произвольную постоянную).

Таблица интегралов

Непосредственно из определения 2 и таблицы производных получаем таблицу интегралов. Справедливость приведенных в ней формул легко проверить дифференцированием (т.е. установить, что производная от правой части равняется подынтегральной функции).

1.

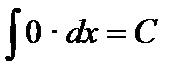
2. ,

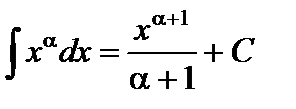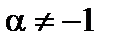
3.

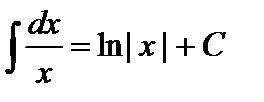
4.

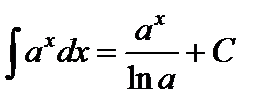
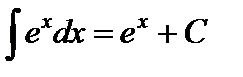
5.

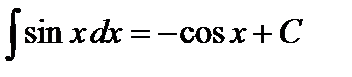
6.

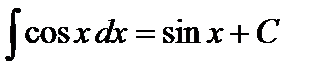
7.

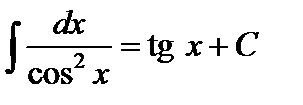
8.

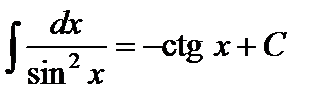
9.

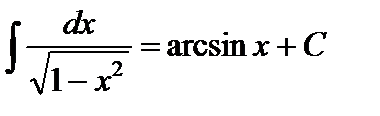
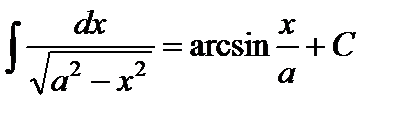
10.

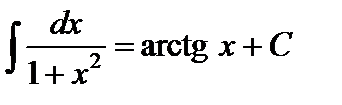
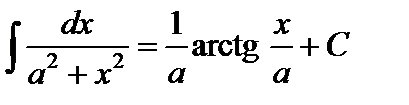
11.

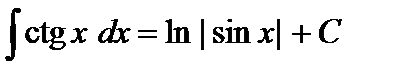
12.

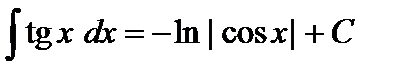
13.

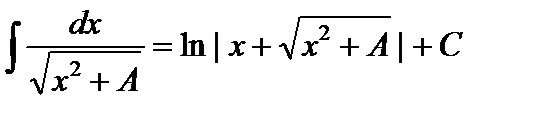
14. .

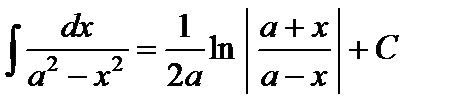К приведенным выше формулам следует добавить еще правила интегрирования, основанные на свойствах неопределенного интеграла.

Простейшие правила интегрирования

I. Постоянный множитель можно выносить за знак интеграла, т.е. если a = const, то

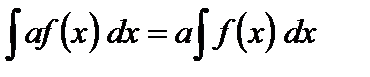
II. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций:

.

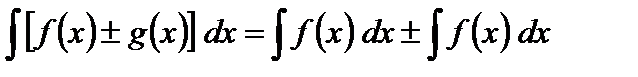III. Если 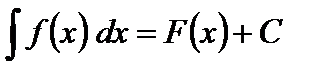, то

.

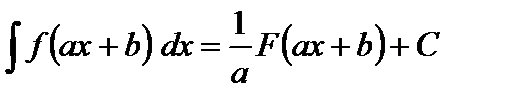Правила I и II очевидны. Убедимся в справедливости правила III:

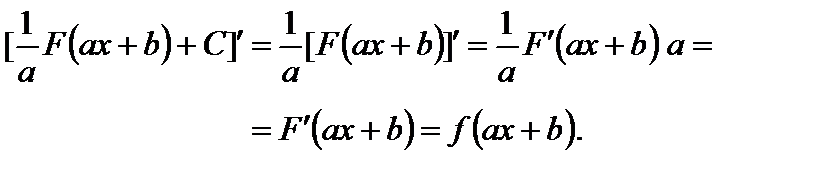
Рассмотрим примеры применения правила III.

Пример 1.

.

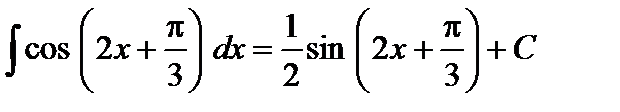Пример 2.

.

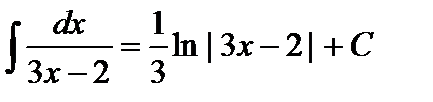Основные методы интегрирования

К основным методам интегрирования относятся: непосредственное интегрирование, интегрирование методом подстановки и интегрирование по частям.

Непосредственное интегрирование

Вычисление интегралов путем непосредственного приложения простейших правил интегрирования и табличных интегралов называется непосредственным интегрированием.

Покажем это на примерах.

1.

.

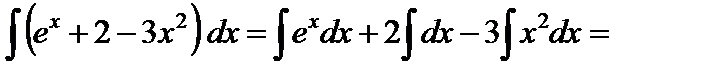
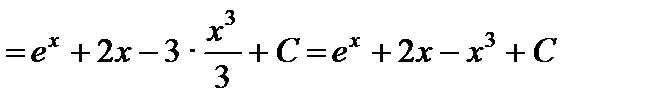2.

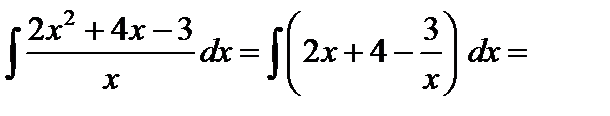
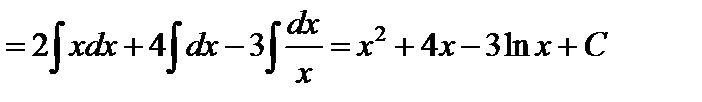
3.

.

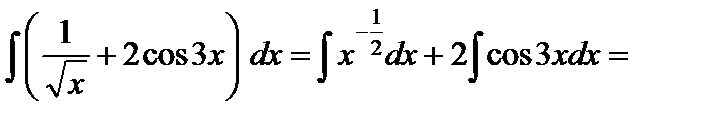
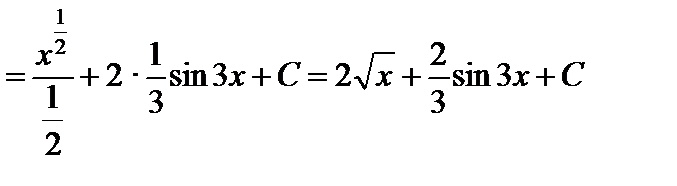Метод подстановки

Одним из самых эффективных методов приведения неопределенного интеграла к табличному является замена переменной интегрирования. Такой метод называется методом подстановки, или методом замены переменной. Он описывается следующей формулой:

,

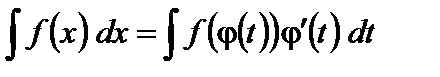где 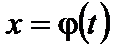– функция, дифференцируемая на рассматриваемом промежутке.

Рассмотрим примеры:

Пример 1. Вычислить .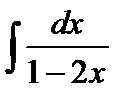

Решение. 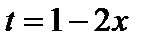. Тогда , ;

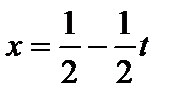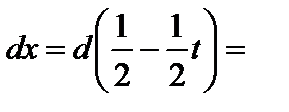
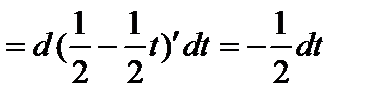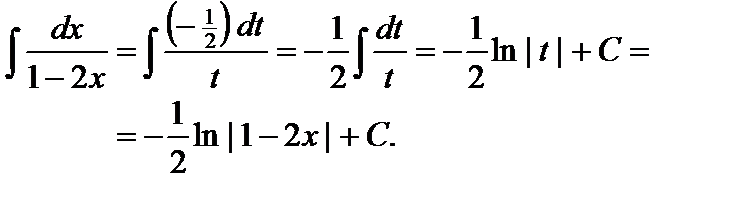
Пример 2. Вычислить .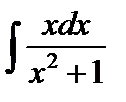

Решение. Положим 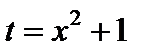. Тогда 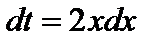. Получаем

.

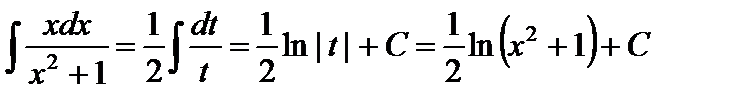Пример 3. Вычислить .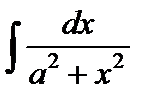

Решение. Положим 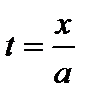; тогда , ;

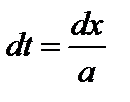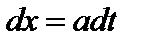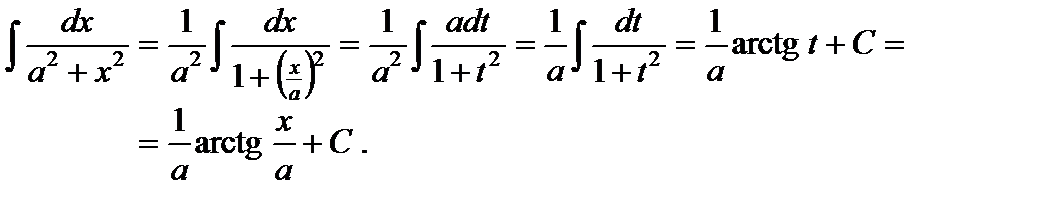
Пример 4. Вычислить .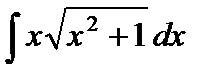

Решение. Положим ; , ;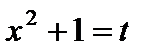

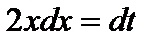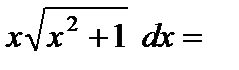
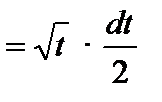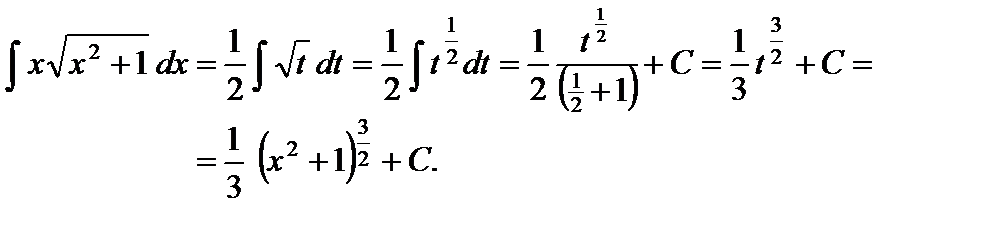
Интегрирование по частям

Пусть 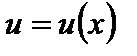, 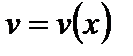– дифференцируемые функции. Тогда

.

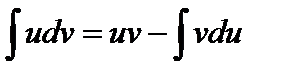Эта формула называется формулой интегрирования по частям. Она непосредственно выводится из формулы .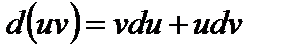

Рассмотрим примеры:

Пример 1. Вычислить .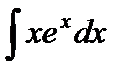

Решение. Положим 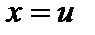, 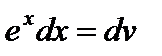. Тогда , ;

.

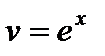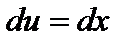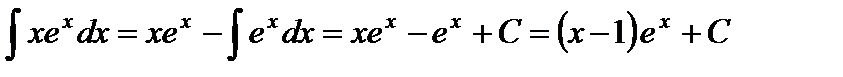Пример 2. Вычислить .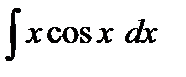

Решение. Положим 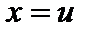, 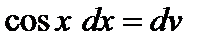; тогда , ;

.

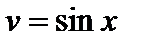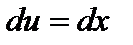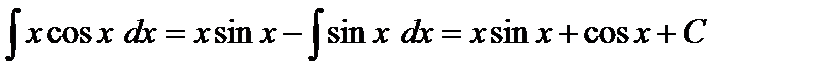Пример 3. Вычислить .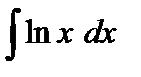

Решение. Положим , ; , ;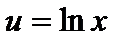

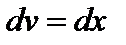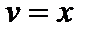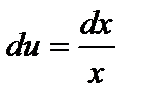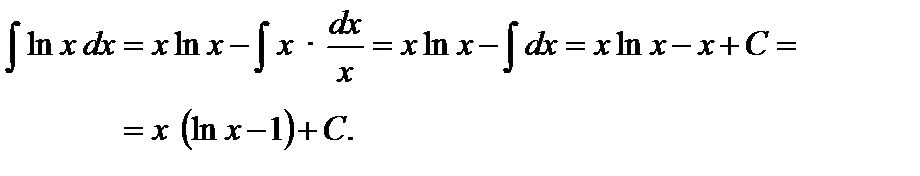
В некоторых случаях для вычисления интеграла формулу интегрирования по частям приходится применять несколько раз.

Пример 4. Вычислить .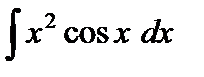

Решение. Положим 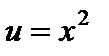, 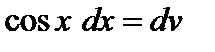; тогда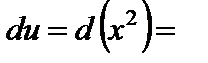 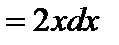, 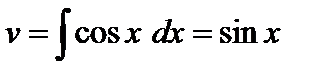. Получаем

.

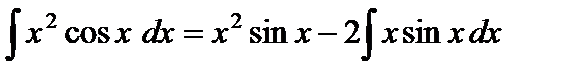Возникший в правой части равенства интеграл не является табличным, однако видно, что мы на правильном пути – интеграл

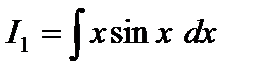
проще исходного. К 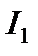снова применим интегрирование по частям, полагая 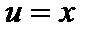, 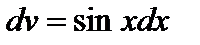; 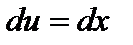, 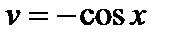. Получаем

.

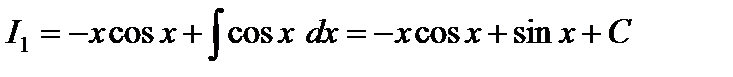Подставляя в (*), находим

.

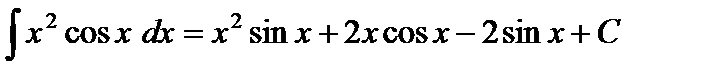Полезно запомнить следующие типы интегралов, которые удобно интегрировать по частям.

I.	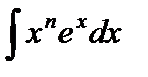IV.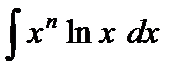
II.	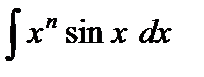V.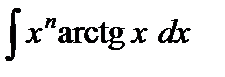
III.	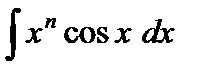VI.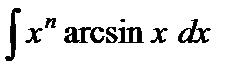

Для нахождения интегралов I–III полагают 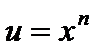. После n-кратного применения метода интегрирования по частям интеграл сведется к табличному.

В интегралах IV–VI полагают 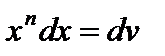.