Замечание по поводу знаков функции

Практика показывает, что наибольшие трудности в методе интервалов возникают на последних двух шагах, т.е. при расстановке знаков. Многие ученики начинают путаться: какие надо брать числа и где ставить знаки.

Чтобы окончательно разобраться в методе интервалов, рассмотрим два замечания, на которых он построен:

1. Непрерывная функция меняет знак только в тех точках, где она равна нулю. Такие точки разбивают координатную ось на куски, внутри которых знак функции никогда не меняется. Вот зачем мы решаем уравнение f (x) = 0 и отмечаем найденные корни на прямой. Найденные числа — это «пограничные» точки, отделяющие плюсы от минусов.
2. Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала. Например, для интервала (−5; 6) мы вправе брать x = −4, x = 0, x = 4 и даже x = 1,29374, если нам захочется. Почему это важно? Да потому что многих учеников начинают грызть сомнения. Мол, что если для x = −4 мы получим плюс, а для x = 0 — минус? А ничего — такого никогда не будет. Все точки на одном интервале дают один и тот же знак. Помните об этом.

Вот и все, что нужно знать про метод интервалов. Конечно, мы разобрали его в самом простом варианте. Существуют более сложные неравенства — нестрогие, дробные и с повторяющимися корнями. Для них тоже можно применять метод интервалов, но это тема для отдельного большого урока.

Теперь хотел бы разобрать продвинутый прием, который резко упрощает метод интервалов. Точнее, упрощение затрагивает только третий шаг — вычисление знака на самом правом куске прямой. По каким-то причинам этот прием не проходят в школах (по крайней мере, мне никто такого не объяснял). А зря — ведь на самом деле этот алгоритм очень прост.

Итак, знак функции на правом куске числовой оси. Этот кусок имеет вид (a; +∞), где a — самый большой корень уравнения f (x) = 0. Чтобы не взрывать мозг, рассмотрим конкретный пример:

(x − 1)(2 + x)(7 − x) < 0;
f (x) = (x − 1)(2 + x)(7 − x);
(x − 1)(2 + x)(7 − x) = 0;
x − 1 = 0 ⇒ x = 1;
2 + x = 0 ⇒ x = −2;
7 − x = 0 ⇒ x = 7;

Мы получили 3 корня. Перечислим их в порядке возрастания: x = −2, x = 1 и x = 7. Очевидно, что наибольший корень — это x = 7.

Для тех, кому легче рассуждать графически, я отмечу эти корни на координатной прямой. Посмотрим, что получится:

Требуется найти знак функции f (x) на самом правом интервале, т.е. на (7; +∞). Но как мы уже отмечали, для определения знака можно взять любое число из этого интервала. Например, можно взять x = 8, x = 150 и т.д. А теперь — тот самый прием, который не проходят в школах: давайте в качестве числа возьмем бесконечность. Точнее, плюс бесконечность, т.е. +∞.

«Ты че, обкурился? Как можно подставить в функцию бесконечность?» — возможно, спросите вы. Но задумайтесь: нам ведь не нужно само значение функции, нам нужен только знак. Поэтому, например, значения f (x) = −1 и f (x) = −938 740 576 215 значат одно и то же: функция на данном интервале отрицательна. Поэтому все, что от вас требуется — найти знак, который возникает на бесконечности, а не значение функции.

На самом деле, подставлять бесконечность очень просто. Вернемся к нашей функции:

f (x) = (x − 1)(2 + x)(7 − x)

Представьте, что x — это очень большое число. Миллиард или даже триллион. Теперь посмотрим, что будет происходить в каждой скобке.

Первая скобка: (x − 1). Что будет, если из миллиарда вычесть единицу? Получится число, не особо отличающееся от миллиарда, и это число будет положительным. Аналогично со второй скобкой: (2 + x). Если к двойке прибавить миллиард, по получим миллиард с копейками — это положительное число. Наконец, третья скобка: (7 − x). Здесь будет минус миллиард, от которого «отгрызли» жалкий кусочек в виде семерки. Т.е. полученное число мало чем будет отличаться от минус миллиарда — оно будет отрицательным.

Осталось найти знак всего произведения. Поскольку в первых скобках у нас был плюс, а в последней — минус, получаем следующую конструкцию:

(+) · (+) · (−) = (−)

Итоговый знак — минус! И неважно, чему равно значение самой функции. Главное, что это значение — отрицательное, т.е. на самом правом интервале стоит знак минус. Осталось выполнить четвертый шаг метода интервалов: расставить все знаки. Имеем:

Исходное неравенство имело вид:

(x − 1)(2 + x)(7 − x) < 0

Следовательно, нас интересуют интервалы, отмеченные знаком минус. Выписываем ответ:

x ∈ (−2; 1) ∪ (7; +∞)

Вот и весь прием, который я хотел рассказать. В заключение — еще одно неравенство, которое решается методом интервалов с привлечением бесконечности. Чтобы визуально сократить решение, я не буду писать номера шагов и развернутые комментарии. Напишу только то, что действительно надо писать при решении реальных задач:

Задача. Решите неравенство:

x(2x + 8)(x − 3) > 0

Заменяем неравенство уравнением и решаем его:

x(2x + 8)(x − 3) = 0;
x = 0;
2x + 8 = 0 ⇒ x = −4;
x − 3 = 0 ⇒ x = 3.

Отмечаем все три корня на координатной прямой (сразу со знаками):

Справа на координатной оси стоит плюс, т.к. функция имеет вид:

f (x) = x(2x + 8)(x − 3)

А если подставить бесконечность (например, миллиард), получим три положительных скобки. Поскольку исходное выражение должно быть больше нуля, нас интересуют только плюсы. Осталось выписать ответ:

x ∈ (−4; 0) ∪ (3; +∞)

Задачи на сплавы и смеси

Задачи на сплавы и растворы удобно решать с помощью таблицы. Порядок заполнения таблицы такой:

1. Сначала решаем, какую величину мы примем за неизвестное, и заполняем тот столбец таблицы, в котором речь идет об этой величине.

2. Заполняем тот столбец, параметры которого даны.

3. Параметры третьего столбца выражаем через параметры первых двух.

Поясню алгоритм решения задачи на сплавы и растворы на примере данной задачи.

1. Поскольку в условии масса первого раствора не указана, примем ее за х. Масса второго раствора равна массе первого и тоже равна х. После того, как растворы смешали, мы получила раствор, масса которого равна2х.

Начнем заполнять таблицу:

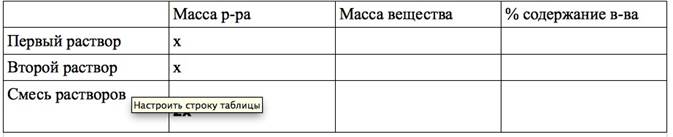
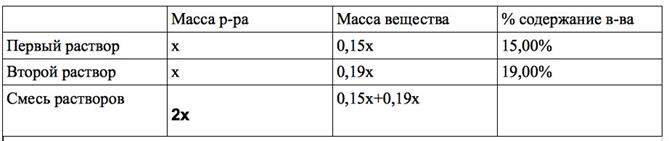
2. В условии задачи дано процентное содержание вещества в каждом растворе. Внесем эти условия в соответствующий столбец таблицы:

3. Параметры второго столбца, то есть массу чистого вещества выразим через параметры первых двух. Для этого воспользуемся формулой:

:

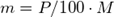Процентное содержание вещества в получившемся растворе равно

массе вещества: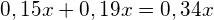

разделить

на массу раствора: ,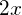

и умножить на 100%

Получим:

% %

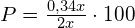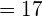Ответ: 17%.

25.

Задачи на движение

Этот раздел посвящен текстовым задачам на движение. В них допускается определенная идеализация: считается, что тела движутся прямолинейно и равномерно, скорости постоянны в течение определенных промежутков времени, не меняются при поворотах и т. д., движущиеся тела считаются материальными точками (если не оговорено противное), т.е. не имеющими размеров и массы (вернее, их размеры и масса несущественны для решения задачи).Основные типы задач на движение:

1) задачи на движение по прямой (навстречу и вдогонку),2) задачи на движение по замкнутой трассе,3) задачи на движение по воде,4) задачи на среднюю скорость,5) задачи на движение протяженных тел.

Рассмотрим более подробно каждый из этих типов задач, выделив, где необходимо, базовые задачи.Движение навстречуОдним из методов решения задач является создание упрощенной модели.Пример 1.Рассмотрим два объекта, движущихся навстречу с указанными на рисунке скоростями. Пусть прошла 1 минута. Как изменилось положение объектов: Видим, что расстояние между объектами сократилось на 15 + 10 = 25 метров. Таким образом, объекты сближаются со скоростью, равной сумме их скоростей. Значит, время их встречи равно t = 100/(15 + 10) = 4 (мин).Если расстояние между двумя телами равно s, а их скорости v₁ и v₂, то время t, через которое они встретятся, находится по формулеt = S/(v₁ + v₂ ).Пример 2.Расстояние между городами А и В равно 435 км. Из города А в город В со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города В выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся? Ответ дайте в километрах.Решение. Через час после выезда первого автомобиля расстояние между автомобилями стало равно 435 - 60 = 375 (км), поэтому автомобили встретятся через времяt = 375/(60 + 65) = 3 (ч)Таким образом, до момента встречи первый автомобиль будет находиться в пути 4 часа и проедет 60 · 4 = 240 (км).Ответ: 240.Движение вдогонкуПример 3.Рассмотрим два объекта, один из которых догоняет другой, с указанными на рисунке скоростями. Пусть прошла 1 минута. Как изменилось положение объектов: Видим, что расстояние между объектами сократилось на 15 – 10 = 5 метров. Т.е. объекты сближаются со скоростью, равной разности их скоростей. Значит, время, за которое первый объект догонит другой, или время их встречи равноt = 100/(15 - 10) = 20 (мин).Если расстояние между двумя телами равно s, и они движутся по прямой в одну сторону со скоростями v₁ и v₂ соответственно (v₁ > v₂) так, что первое тело следует за вторым, то время t, через которое первое тело догонит второе, находится по формуле t = S/(v₁ - v₂ ).Пример 4.Два пешехода отправляются в одном направлении одновременно из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?Решение. Время t в часах, за которое расстояние между пешеходами станет равным 300 метрам, т. е. 0,3 км, находим по формулеt = 0,3/(v + 1,5 - v) = 0,3/1,5 = 0,2 (ч)Следовательно, это время составляет 12 минут.Ответ: 12.Движение по окружности (замкнутой трассе)Пример 5.Рассмотрим движение двух точек по окружности длины L в одном направлении при одновременном старте со скоростями v₁ и v₂ (v₁ > v₂) и ответим на вопрос: через какое время первая точка будет опережать вторую ровно на один круг? Считая, что вторая точка покоится, а первая приближается к ней со скоростью v₁ – v₂, получим, что условие задачи будет выполнено, когда первая точка поравняется в первый раз со второй. При этом первая точка пройдет расстояние, равное длине одного круга, и искомая формула ничем не отличается от формулы, полученной для задачи на движение вдогонку: t = L/(v₁- v₂) .Итак, если две точки начинают движение по окружности в одну сторону со скоростями v₁ и v₂ соответственно (v₁ > v₂), то первая точка приближается ко второй со скоростью v₁ - v₂ и в момент, когда первая точка в первый раз догоняет вторую, она проходит расстояние на один круг больше.Пример 6.Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.Решение.Пусть скорость второго автомобиля х км/ч. Поскольку 40 минут составляют 2/3 часа и это — то время, за которое первый автомобиль будет опережать второй на один круг, составим по условию задачи уравнение14/(80-x) = 2/3, 160 - 2x = 42, т.е. х = 59 (км/ч).Ответ: 59.Движение по водеВ задачах на движение по воде скорость течения считается неизменной. При движении по течению скорость течения прибавляется к скорости плывущего тела, при движении против течения — вычитается из скорости тела. Скорость плота считается равной скорости течения.Пример 7.Теплоход, скорость которого в неподвижной воде равна 25 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 30 часов после отплытия из него. Сколько километров прошел теплоход за весь рейс? Решение.Пусть искомая величина равна 2S.

	S (км)	v (км/ч)	t (ч)
По течению	S	25 + 3 = 28	S/28
Против течения	S	25 – 3 = 22	S/22
Стоянка	-	-

Составим по условию задачи уравнение 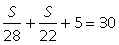,откуда 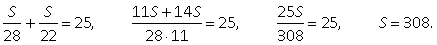.Значит, искомое расстояние равно 616 км.Ответ: 616.Средняя скоростьНапомним, что средняя скорость вычисляется по формуле 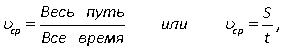где S — путь, пройденный телом, a t — время, за которое этот путь пройден. Если путь состоит из нескольких участков, то следует вычислить всю длину пути и всё время движения. Например, если путь состоял из двух участков протяженностью S₁ и S₂, скорости на которых были равны соответственно v₁ и v₂, то 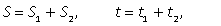где 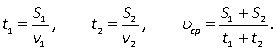Пример 8.Первую треть трассы велосипедист ехал со скоростью 12 км/ч, вторую треть — со скоростью 16 км/ч, а последнюю треть — со скоростью 24 км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути. Ответ дайте в км/ч.Решение.Обозначим длину всей трассы через 3S. Тогда первую треть трассы велосипедист проехал за время t₁ = S/12, вторую треть — за время t₂ = S/16, последнюю треть — за время t₃ = S/24. Значит, время, потраченное им на весь путь, равно t₁ + t₂ + t₃,т. е. 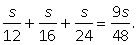Поэтому искомая средняя скорость находится по формуле 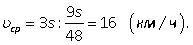Ответ: 16.Движение протяженных тел

В задачах на движение протяжных тел требуется определить длину одного из них. Наиболее типичные ситуации: определение длины поезда проезжающего мимо

• придорожного столба
• идущего параллельно путям пешехода
• лесополосы определенной длины
• другого двигающегося поезда

Если поезд движется мимо столба (светофора, человека), то он проходит расстояние S равное его длине L:S = L = vt.Если поезд движется мимо протяженной лесополосы, то он проходит расстояние равное сумме длины самого поезда L₁ и лесополосы L₂ :S = L₁ + L₂.Пример 9.Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 30 секунд. Найти длину поезда в метрах.Решение.Зная скорость движения v = 60 км/ч = 1000 м/мин и время, за которое он проезжает мимо столба t = 30 сек. = 1/2 мин, можно найти длину поезда как пройденное расстояние S = vt = 1000·1/2 = 500 (м).Ответ: 500.Пример 10.Поезд, двигаясь равномерно со скоростью 90 км/ч, за 1 минуту проезжает мимо лесополосы, длина которой 800 м. Найти длину поезда в метрах.Решение.Зная скорость движения v = 90 км/ч = 1500 м/мин и время, за которое он проезжает мимо лесополосы длиной 800 метров за t = 1 мин, можно найти длину поезда как пройденное расстояние S = vt = 1500·1 = 1500 м минус длина лесополосы 800 метров и получим длину поезда равную 700 метров.Ответ: 700.Пример 11.Поезд проходит мост длиной 450 м за 45 с, а мимо будки стрелочника — за 15 с. Найти длину поезда и его скорость.Решение.Пусть скорость поезда v м/с. Тогда длина поезда L = 15v (м). За 45 с поезд проходит расстояние 45v (м) или (450 + 15v) м. Получаем уравнение:45v = 450 + 15v, откуда v = 15, L = 15v = 225.Ответ: длина поезда 225 м, а его скорость 15 м/с.Пример 12.По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго сухогруза составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?Решение. 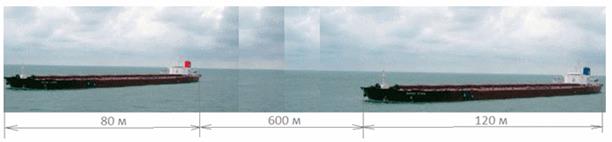Через 12 минут: Будем считать, что первый сухогруз неподвижен, а второй приближается к нему со скоростью х (м/мин), равной разности скоростей второго и первого сухогрузов. Тогда за 12 минут второй сухогруз проходит расстояние L = 400 + 120 + 80 + 600 = 1200 (м).Поэтому х = 1200/12 = 100 (м/мин) = 6 (км/ч).Ответ: 6.Задачи для тренировкиУсловие задач часто для удобства представляют либо в виде рисунка, либо в виде таблицы, либо в виде того и другого.Пример 13.Расстояние между двумя городами скорый поезд проходит на 4 часа быстрее товарного и на 1 час быстрее пассажирского. Найти скорости товарного и скорого поездов, если известно, что скорость товарного поезда составляет 5/8 от скорости пассажирского и на 50 км/ч меньше скорости скорого.Решение.Пусть v км/ч — скорость товарного поезда (v > 0), t ч — время движения скорого поезда (t > 0). Составим таблицу.

	Расстояние (км)	Скорость (км/ч)	Время (ч)
Скорый поезд	(v+50)t	v+50	t
Пассажирский поезд	8/5 v(t+1)	8/5 v	t+1
Товарный поезд	v(t+4)	v	t+4

По условию задачи поезда прошли одно и то же расстояние. Получаем цепочку (систему) уравнений (v + 50)t = 8/5 v(t + 1) = v(t + 4).vt + 50t = vt + 4v 50t = 4v 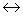v = 12,5t,1,6vt + 1,6v = vt + 4v 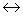0,6vt = 2,4v |: v > 0 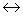t = 4, v = 12,5 · 4 = 50.50 км/ч — скорость товарного поезда.50 + 50 = 100 (км/ч) — скорость скорого поезда.Ответ: 50, 100.Пример 14.Два туриста вышли одновременно навстречу друг другу из пунктов А и В. Каждый шел с постоянной скоростью и, придя, в конечный пункт, немедленно поворачивал обратно. Первый раз они встретились в 12 км от пункта В, второй раз — в 6 км от А через 6 часов после первой встречи. Найти расстояние между пунктами и скорости туристов.Решение.Используя схему движения туристов, составим таблицу.

Туристы/Путь	S	v	t
I	АС	6 + S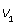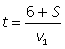
СВ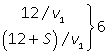
ВД	12 + S
II	ВС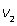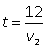
СА	6 + S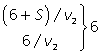
АД

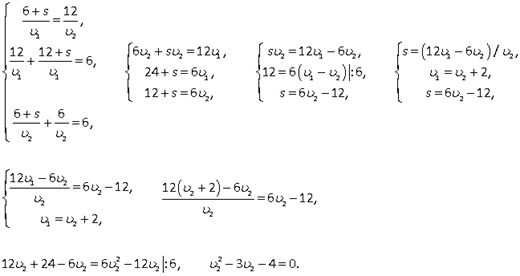Из корней последнего уравнения (-1 и 4) только v₂ = 4 (км/ч) походит по смыслу. Тогда v1 = v2 + 2 = 4 + 2 = 6 (км/ч).S = 6v₂ - 12 = 24 – 12 = 12 (км).Весь путь 18 + S = 18 + 12 = 30 (км).Ответ: 30, 4, 6.В следующей задаче встречается два типа задач: «движение навстречу» и «обычное движение».Пример 15.Два велосипедиста выехали одновременно из пунктов А и В навстречу друг другу. Велосипедист, ехавший из А, прибыл в В через 4 часа после встречи, а велосипедист, ехавший из В, прибыл в А через 9 часов после встречи. Сколько часов был в пути каждый велосипедист?Решение.Пусть весь путь от А до В равен S км, v₁ и v₂ — скорости велосипедистов и t_в — время, прошедшее с момента начала движения до встречи велосипедистов.

	S	v	t
I до встречи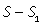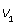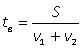
II до встречи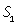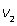
I после встречи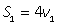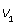
II после встречи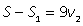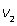

Первый и второй велосипедисты после встречи проехали весь путь S, который найдем из выражений для S₁ и S - S₁ :S = S₁ + (S - S₁ ) = 4v₁ + 9v₂, тогда выражение для t_в : t_в = (4v₁ + 9v₂)/( v₁ + v₂). Имеем систему уравнений: 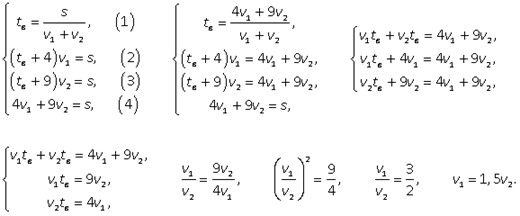Тогда 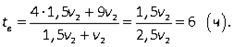Тогда значения времени, о которых спрашивается в задаче: t_в + 4 = 10 ч, t_в + 9 = 15 ч.

Задачи на пропорцию

Задача 1. Толщина 300 листов бумаги для принтера составляет 3, 3 см. Какую толщину будет иметь пачка из 500 листов такой же бумаги?

Решение. Пусть х см — толщина пачки бумаги из 500 листов. Двумя способами найдем толщину одного листа бумаги:

3,3:300 или х:500.

Так как листы бумаги одинаковые, то эти два отношения равны между собой. Получаем пропорцию (напоминание: пропорция — это равенство двух отношений):

3,3:300=х:500. Неизвестный средний член пропорции равен произведению крайних членов пропорции, деленному на известный средний член. (Подробно о пропорции и нахождению ее крайнего, среднего членов читайте в статье: Пропорция. Основное свойство пропорции.»

х=(3,3·500):300;

х=5,5. Ответ: пачка 500 листов бумаги имеет толщину 5,5 см.

Это классическое рассуждение и оформление решения задачи. Такие задачи часто включают в тестовые задания для выпускников, которые обычно записывают решение в таком виде:

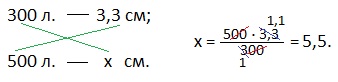
или решают устно, рассуждая так: если 300 листов имеют толщину 3,3 см, то 100 листов имеют толщину в 3 раза меньшую. Делим 3,3 на 3, получаем 1,1 см. Это толщина 100 листовой пачки бумаги. Следовательно, 500 листов будут иметь толщину в 5 раз большую, поэтому, 1,1 см умножаем на 5 и получаем ответ: 5,5 см.

Разумеется, это оправдано, так как время тестирования выпускников и абитуриентов ограничено. Однако, на этом занятии мы будем рассуждать и записывать решение так, как положено это делать в6 классе.

Задача 2.Сколько воды содержится в 5 кг арбуза, если известно, что арбуз состоит на 98% из воды?

Решение.

Вся масса арбуза (5 кг) составляет 100%. Вода составит х кг или 98%. Двумя способами можно найти, сколько кг приходится на 1% массы.

5:100 или х:98. Получаем пропорцию:

5:100 = х:98.

х=(5·98):100;

х=4,9 Ответ: в 5кг арбуза содержится 4,9 кг воды.

Задача 3.Масса 21 литра нефти составляет 16,8 кг. Какова масса 35 литров нефти?

Решение.

Пусть масса 35 литров нефти составляет х кг. Тогда двумя способами можно найти массу 1 литра нефти:

16,8:21 или х:35. Получаем пропорцию:

16,8:21=х:35.

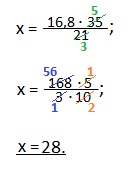Находим средний член пропорции. Для этого перемножаем крайние члены пропорции (16,8 и 35) и делим на известный средний член (21). Сократим дробь на7.

Умножаем числитель и знаменатель дроби на 10, чтобы в числителе и знаменателе были только натуральные числа. Сокращаем дробь на5(5 и 10) и на 3 (168 и 3).

Ответ: 35 литров нефти имеют массу 28 кг.

Задача 4. После того, как было вспахано 82% всего поля, осталось вспахать еще 9 га. Какова площадь всего поля?

Решение.

Пусть площадь всего поля х га, что составляет 100%. Осталось вспахать 9 га, что составляет 100% — 82% = 18% всего поля. Двумя способами выразим 1% площади поля. Это:

х:100 или 9:18. Составляем пропорцию:

х:100 = 9:18.

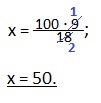Находим неизвестный крайний член пропорции. Для этого перемножаем средние члены пропорции (100 и 9) и делим на известный крайний член (18). Сокращаем дробь.

Ответ: площадь всего поля 50 га.