Знакочередующийся ряд. Признак Лейбница.

Знакочередующийся ряд можно записать в виде a₁-a₂+a₃-a₄+…+(-1)ⁿ⁺¹a_n+…, (1) где a_n>0. Признак сходимости Лейбница: теорема: Если абсолютные величины членов знакочередующегося ряда (1) монотонно убывают: a₁>a₂>a₃>…и общий член ряда стремится к нулю: lim a_n = 0, то ряд сходится.

n®¥

Док-во: Пусть дан ряд (1) и пусть a_n>a_n+1 и a®0 при n®¥. Рассмотрим частичную сумму ряда с чётным числом членов S_2n=a₁-a₂+a₃-a₄+…+a_2n-1-a_2n=(a₁-a₂)+(a₃-a₄)+…+(a_2n-1-a_2n). Все разности в скобках в силу первого условия положительны, поэтому последовательность частичных сумм {S_2n}является возрастающей. Докажем, что она ограничена. Для этого представим S_2n в виде

S_2n=a₁-[(a₂-a₃)+(a₄-a₅)+…+(a_2n-2-a_2n-1)+a_2n]. Отсюда следует, что S_2n<a₁ для любого n, т.е. {S_2n} ограничена. Итак, последовательность {S_2n} возрастающая и ограниченна, следовательно, она имеет предел lim S_2n=S.

n®¥

Покажем теперь, что и последовательность частичных сумм нечётного числа членов сходится у тому же пределу S. Действительно, S_2n+1=S_2n+a_2n+1. Переходя в этом равенстве к пределу при n®¥ и используя второе условие (a_n®0 при n®¥) , получаем:

lim S_2n+1 = lim (S_2n + a_2n+1) = lim S_2n + lim a_{2 +1} = S + 0 = S.

n®¥ n®¥ n®¥ n®¥

Таким образом, последовательность частичных сумм ряда (1) сходится к пределу S. Это и означает, что ряд (1) сходится.

Знакопеременные ряды, их сходимость.

Знакопеременный ряд: a₁ + a₂ +a₃+…+a_n+…= åa_n (1), где числа а₁…могут быть как

n=1

положительными, так и отрицательными, причём расположение положительных и отрицательных членов в ряде произвольно. Одновременно рассматривается ряд, составленный из абсолютных величин членов ряда (1):

¥

½а₁½+½а₂½+½а₃½+…+½а_n½+…=å½а_n½ (2).Такой признак сходимости – теорема:

Если ряд (2) сходится, то сходится и ряд (1).

Док-во: пусть ряд (2) сходится. Обозначим через S_n частичную сумму ряда (1), а через s_n частичную сумму ряда (2): S_n= a₁ + a₂ +a₃+…+a_n; s_n =½а₁½+½а₂½+½а₃½+…+½а_n½.Так как ряд (2) сходится, то последовательность его частичных сумм {s_n} имеет предел lim s_n=s, при этом для любого n имеет место неравенство s_n £s (3), поскольку члены ряда (2) неотрицательны.

Обозначим через S’_n сумму положительных членов, а через S’’_n сумму модулей отрицательных членов, содержащихся в сумме S_n . Тогда: S_n = S’_n - S’’_n(4), s_n = S’_n + S’’_n (5). Очевидно, последовательности { S’_n } и { S’’_n } не убывают, а из равенства (5) и неравенства (3) следует, что они являются ограниченными: S’_n £s_n £s и S’’_n £s_n £s. Следовательно, существуют lim S’_n = S’ и lim S’’_n = S’’. Но в таком случае, в

n®¥ n®¥

силу равенства (4), последовательность частичных сумм ряда (1) имеет предел :

lim S_n = lim ( S’_n - S’’_n)= lim S’_n - lim S’’_n = S’_n – S’’_n.

n®¥ n®¥ n®¥ n®¥

Это означает, что ряд (1) сходится.

Степенные ряды.

¥

Ряд вида a₀ + a₁x +a₂x² +a₃x³+…+a_nxⁿ+…=åa_nxⁿ (1) называется степенным рядом.

n=0

Числа a₀, a_1, a_2,…,a_n,… называются коэффициентами степенного ряда.

Придавая х различные числовые значения , будем получать различные числовые ряды, которые могут оказаться сходящимися или расходящимися. Множество тех значений х , при которых ряд (1) сходится, называется областью его сходимости. Это множество всегда не пусто, т.к. любой степенной ряд сходится при х=0. Очевидно, что частичная сумма S_n (х)= a₀ + a₁x +…+a_nxⁿ является функцией переменной х. Поэтому и сумма ряда S также является некоторой функцией переменной х, определённой в области

сходимости ряда:

¥ ¥

S=S(x)= åa_nxⁿ (или f(x)= åa_nxⁿ).

n=0 n=0

Теорема Абеля.

1) Если степенной ряд (1) сходится при х=х₀ (х₀¹ 0), то он сходится, и притом абсолютно, для всех х, удовлетворяющих условию я½ х½<½ х₀½.

2) Если ряд (1) расходится при х= х₁,то он расходится для всех х, удовлетворяющих условию ½х½<½х₁½.

¥

Док-во: 1)т.к. по условию числовой ряд åa_nx₀ⁿ сходится, то его общий член a_nx₀ⁿ ®0 при

n=0

n®¥, откуда следует, что последовательность { a_nx₀ⁿ } ограничена , т.е. существует число M>0 такое, что ½ a_nx₀ⁿ ½<M, n =0, 1, 2… (2) Перепишем ряд (1) в виде

a₀ + а₁х₀ (х/х₀) + а₂х²₀ (х/х₀)² +…+ а_n хⁿ₀ (х/х₀)ⁿ +… (3) и рассмотрим ряд, составленный из абсолютных величин его членов : ½a₀½+ ½а₁х₀½½х/х₀½ + ½а₂х²₀½½х/х₀½² +…+ ½а_n хⁿ₀½½х/х₀½ⁿ +… (4).

Члены ряда (4) в силу неравенства (2) меньше соответствующих членов ряда

М+ М½х/х₀½ + М½х/х₀½² +…+М½х/х₀½ⁿ +… (5) При ½ х½<½ х₀½ ряд (5) представляет собой геометрическую прогрессию со знаменателем q=½х/х₀½<1 и, следовательно, сходится.

Т.к. члены ряда (4) меньше соответствующих членов ряда (5) то, по признаку сравнения, ряд (4) также сходится, а это значит, что ряд (1) при ½ х½<½ х₀½ сходится абсоютно.

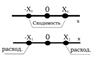По условию, в точке x₁ ряд (1) расходится. Требуется показать, что он расходится для всех x , удовлетворяющих условию ½ х½>½ х₁½. Предположим обратное, т.е. допустим, что при некотором значении х таком, что ½ х½>½ х₁½, ряд (1) сходится. Тогда по только что доказанной первой части теоремы ряд (1) должен сходиться и в точке х₁, т.к. ½ х₁½<½ х½. Но это противоречит тому, что в точке х₁ ряд расходится.

Теорема Абеля утверждает, что если х₀ – точка сходимости степенного ряда, то во всех точках, расположенных на интервале (-½х₀½,½ х₀½), этот ряд сходится абсолютно, а если х₁ – точка расходимости степенного ряда, то во всех точках, расположенных вне интервала (-½х₁½,½ х₁½), ряд расходится.