Определение числового ряда, частичной суммы, сходящегося ряда.
Рассмотрим производную числовую последовательность а1, а2,….аn, …
Формально из элементов этой последовательности составим сумму а1+а2+а….+аn=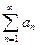 
Такую сумму принято называть числовым рядом или просто рядом а1,а2,…аn, … элементы члены ряда
An – общий член ряда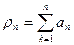 
Сумма первых n членов ряда называется частичной суммой n-переменных
Если для данного ряда предел последовательности частичных сумм не сущетствует, то такой рад называется расходящимся.
Свойства сходящихся числовых рядов.
10 Отбрасывание конечного числа членов ряда не влияет на сходимость(расходимость) ряда
20 Если ряд а1+а2+…..+аn+…..=3n=1%аn сходится и имеет сумму S то сход. Также и ряд 3n=1%kan, где k не равняется 0 и постоянное число, при чём сумма этого ряда равна kS
30 Если ряды 3n=1%аn и 3n=1% bn сходятся и суммы их соответственно равны S’ и S”, то и ряд 3n=1%(аn" bn) также сходится , при чём его сумма S=S’"S”
20 и 30 следуют из соответствующих свойств сходящихся последовательностей
40 Общий член аn сходящегося ряда стремиться к 0 при n®0
Необходимое условие сходимости числового ряда. Сходимость гармонического ряда.
Т.Если ряд сходится, то его общий член стремится к 0.
аn=Sn-Sn-1 и, поскольку ряд сход., Sn®S и Sn-1®S при n®¥, где S- сумма ряда отсюда и след. Справедл. Данного св., кот. Наз. Необх. Услов. Сход. Ряда(если оно не соблюдается то ряд расходится)
Замеч. 40 явл. необх. Усл. , но не явл. достаточн. ,т.е. по нему нельзя провер. сход. ряда
Сходимость Гармонического ряда
1+1/2+1/3+1/4+…..+1/n+…..=3n=1%1/n
lim nY%1/n=0, но тем не менее этот ряд расход.
П.п. гармонич. Ряд сходится:
lim nY%S2n=S
lim nY%Sn=S
S2n- Sn
lim nY%(S2n- Sn)=S-S=0
S2n- Sn=1/(n+1)+1/(n+2)+…..+1/2n>1/2n+1/2n+1/2n+1/2n=n*2n=1/2
Мы пришли к противоречию,Y гармонич. Ряд расходится.
Необходимое и достаточное условие сходимости ряда с неотрицательными членами.
Необходимое и достаточное условие сход. Числового ряда с неотриц. Членами
Пусть 3n=1%an и любой аn$0
Тm. Для того, чтобы ряд с неотриц. Членами сходился н. и д. , чтобы послед. Частичных сумм {Sn} этого ряда была ограниченной.
Доказ. Необходимость: пусть ряд 3n=1%an сходится, тогда по опред послед. Частичных сумм {Sn} также сходится, следовательно по tm всякая сходящаяся послед. Ограничена
Достаточность: пусть {Sn} – ограниченная последовательность ,т.к. любой аn$0, то 0#S1#S2#…..#Sn, т.е. послед. Монотонная неубывающая, по tm всякая Монотонная неубывающая последовательность сходится и ряд также сходится
Признак сравнения.
Пусть для двух рядов си неотрицательными членами 
(1)и 
(2)выполняется неравенство a£b для всех n. Тогда из сходимости ряда (2) следует сходимость ряда (1), а расходимость ряда (1) влечет за собой расходимость ряда (2)
Доказательство: Пусть Sn и Sn’ частичные суммы соответственно рядов 1 и 2. Из условия теоремы следует, что Sn£Sn’ Если ряд 2 сходится, то по теореме о необходимом и достаточном условии сходимости ряда последовательность {Sn’} ограничена, значит, монотонная последовательность {Sn} также ограничесна, т.е. она также сходится. Если ряд 1 расходится, то ряд 2 не может сходиться, иначе в силу первой части доказательства будет сходится и ряд 1. ч.т.д.
Замечание: для того, чтобы проверить сходимость-расходимость числового ряда его надо сравнить с заведомо сходящимся рядом *например бесконечно убывающей геометрической прогрессией) или заведомо расходящимся (например с грамоническим рядом или бесконечной программой с q>1)
41.
 |
Признак Даламбера.
Пусть дан ряд åan (111) с положительными членами и существует
n=1
предел lim ((an+1)/(an))=r. Тогда:
n®¥
а) при r<1 ряд сходится; б) при r>1 ряд расходится.
Док-во: а) Пусть r<1 и lim ((an+1)/(an))=r. Докажем, что ряд (111)
n®¥
сходится. .По определению предела числовой последовательности для любого e>0 существует номер N такой, что при n³N выполняется неравенство ½(an+1)/(an) - r½< e. Отсюда следует, что r-e< (an+1)/(an)<r+e (1). Т. к. r<1, то e можно взять настолько малым, что будет выполнено неравенство r+e<1. Полагая r+e= q, на основании правого из неравенств (1) имеем (an+1)/(an)<q, или an+1 < anq для n=N, N+1, N+2… (2) Придавая n эти значения, из последнего неравенства получаем aN+1<aNq, aN+2<aN+1q< aNq2, aN+3<aN+2q< aNq3, …….., т.е. члены ряда aN+1+aN+2+ aN+3+… меньше соответствующих членов ряда, составленного из элементов геометрической прогрессии: aNq+ aNq2+ aNq3+… (3). Так как q<1 , то ряд (3) сходится. Но ряд (2) получен из данного ряда (111 ) в результате отбрасывания конечного числа первых членов, след-но, по теореме о свойстве сходящихся рядов ряд (111) сходится.
б) Пусть теперь r>1. Докажем, что ряд (111) расходится. Возьмём e настолько малым, чтобы r-e<1. Тогда при n³N в силу левого из неравенств (1) выполняется неравенство (an+1)/(an)>1 или an+1> an. Таким образом, члены ряда , начиная с некоторого номера N , возрастают с увеличением их номеров, т.е. общий член ряда an не стремится к нулю при n®¥. Следовательно, по теореме о необходимом условии сходимости ряда, ряд (111) сходится.
Замечание. При r=1, как показывают примеры, ряд (111) может как сходиться, так и расходиться. В этом случае необходимо дополнительное исследование ряда с помощью др. признаков.
42. Интегральный признак Коши.¥
Пусть дан ряд f(1)+f(2)+f(3)+…+f(n)+…= åf(n)
n+1 (222) , члены которого являются значениями некоторой функции f(x , положительной, непрерывной и убывающей на +¥
полуинтервале [1, +¥). Тогда, если ò f(x)dx (333) сходится, то сходится и
1
ряд (222).Если же (333)расходится , то и ряд (222) также расходится.
Док-во: Рассмотрим криволинейную трапецию, ограниченную сверху графиком функции y=f(x), с боковых сторон прямыми x=1, x=n, снизу осью Ох. Впишем в эту трапецию и опишем около нее две ступенчатые фигуры, состоящие из прямоугольников с основаниями [1,2], [2,3],…, [n-1,n] и высотами f(1), f(2), f(3),…, f(n-1), f(n). Тогда, принимая во внимание геометрический смысл определённого интеграла, имеем
n
f(2)+f(3)+…+f(n)<òf(x)dx (444)<f(1)+f(2)+…+f(n-1) , или, короче,
n 1
Sn-f(1)<òf(x)dx<Sn-f(n).
1 n n
Отсюда получаем: Sn<f(1) + òf(x)dx (1), Sn>f(n) + òf(x)dx (2) ,где Sn –
1 1
частичные суммы рассматриваемого ряда. Пусть интеграл (444) сходится. Это значит, что существует lim (444)=I.
n®¥ Так как f(x)>0, то последовательность (444) возрастает с увеличением n и ограничена сверху своим пределом: (444)<I. Из неравенства (1) следует , что Sn<f(1) + I, т.е. последовательность частичных сумм {Sn} ряда (222) ограничена. По теореме о необходимом и достаточном условиях сходимости ряда с неотрицательными членами ряд (222) сходится.
Пусть теперь интеграл (333) расходится. В этом случае (444)®+¥ при n®¥ (как монотонно возрастающая неограниченная последовательность). Из неравенства (2) следует, что Sn®+¥ при n®¥, т.е. последовательность частичных сумм {Sn} ряда (222) расходится и, следовательно, ряд расходится.