Приближенное вычисление определенного интеграла.

Пусть в интеграле 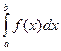функция f(x) непрерывна на отрезке [a,b]. Разобьем этот отрезок на n равных частей точками (узлами) х=х_i (0£I£n). Проведем прямые х=х_i и соединим соседние точки их пересечения с кривой f(x) хордами, т.е. построим n трапецией с основаниями y_i-1=f(x_i-1) и y_i=f(x_i) и высотой (b-a)/n каждая (0£I£n). Сумма площадей этих прямоугольных трапеций приближенно равна площади криволинейной трапеции или искомому интегралу: = ]

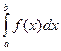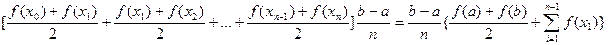Это формула трапеции.

B

A

f(x₀) f(X₁) f(X₂) f(x _k-1) f(X_k) f(x _n-1) f(Xn)

X₀=a X₁ X₂ X _k-1 X_k X _n-1 b=Xn

Несобственные интегралы с бесконечными пределами.

Несобственные интегралы.

При рассмторении определенного интеграла как предела интегральных сумм предполагалось, что подынтегральная функция ограничена на конечном отрезке интегрирования. Данное выше определение определенного интеграла не имеет смысла, если не выполняется хотя бы одно из этих условий. Нельзя разбить бесконечный интервал на конечное число отрезков конечной длины, при неограниченной функции интегральная сумма не имеет предела.

В связи с этим вводят понятие несобственного интеграла 1 и 2 рода.

Интегралы с бесконечными пределами интегрирования.

Пусть функция f(x) определена на промежутке [a; +¥) и интегрируема на любом отрезке [a,R], R>0, так что интеграл 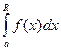имеет смысл, Предел этого интеграла при R®¥ называется несобственным интегралом первого рода и обозначается 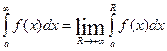. В случае, если этот предел конечен, говорят, что несобственный интеграл сходится, а функцию f(x) называют интегрируемой на бесконечном промежутке [a, +¥), если же предел бесконечен или не существует, то говорят, что несобственный интеграл расходится.

Аналогично вводится понятие несобственного интеграла по промежутку (-¥, b]. 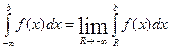. Наконец, несобственный интеграл с двумя бесконечными пределами можно определить как сумму несобственных интегралов 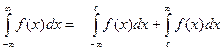, где с- любое число.

Геометрический смысл несобственного интеграла первого рода основан на геометрической интерпретации определенного интеграла на отрезке [a,R]: это площадь бесконечной области, ограниченной сверху неотрицательной функцией f(x), снизу осью Ох, слева- прямой х=а. Такая же интерпретация имеет место и для остальных несобственных интегралов.

. y=f(x)

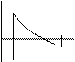А R

Несобственные интегралы от неограниченных функций.

Интегралы от неограниченных функций

Рассмотрим функцию f(x), определенную на промежутке [a,b), но неограниченную на нем. Для определенности положим, что f(x) ограничена и интегрируема на любом отрезке [a,b-e], 0< e<b-a, но неограниченна в любой окрестности точки b или на промежутке [b-e,b]. В таком случае b называется особой точкой.

DEF

Предел интеграла 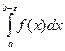при e®0 называется несобственным интегралом второго рода и обозначается 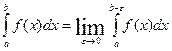. Если этот предел конечный, то говорят что интеграл существует или сходится, а функцию f(x) называют интегрируемой на промежутке [a,b), если предела нет или он бесконечен, то говорят что интеграл расходится. Аналогично, если особой является точка х=а, то несобственных интеграл второго рода определяется как 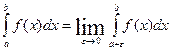Если функция f(x) не ограничена в окрестности некоторой внутренней точки сÎ[a,b], то по определению полагают 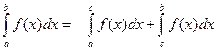, где несобственные интегралы второго рода в правой части этого равенства определяются соответственно по формулам предыдущим. Если а и b особые точки, т.е. функция f(x) ограничена и интегрируема на интервале (a,b), то несобственный интеграл второго рода определяется в виде суммы 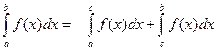, где с- произвольная точка на (a,b), а несобственные интегралы второго рода в правой части этого равенства определяются соответственно по формулам.

19. Метрические, линейные, нормированные, евклидовы пространства.

Функции многих переменных:

Пусть у=f(x), D(f)=XÌR, Е(f)=YÌR

Y=f(x1, x2, … xn) это точки n-мерного Эвклидового пространства

Метрические пространства.

На множестве Х определена фигура метрического пространства, если задана функция r(x,y) двух произвольных элементов этого множества, удовлетворяющих следующим аксиомам:

1. 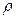(x,y)=0 тогда и только тогда, когда x=y

3. r(x,y)£r(x,z)+r(z,y) (неравенство )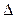

r(х,y) функция метрики или функция расстояния между точками х и у, принадлежащих Х.

Т.о. метрическое пространство R образует множество Х, с введенной на этом множестве функции расстояния метрического пространства R=(X, r). Если положим, что х=у, то 0£r(x,z)+r(z,y)

Р(x,y) функция метрики или функция расстояния между точками х и у, принадлежащих Х. Т.о. метрическое пространство R образует множество Х, связанной на этом множестве функции расстояния метрического пространства R=(X,р)

Если положим, что х=у, то 0£р(xz)+p(z,x)

2p(x,z)>0 метрика не отрицательна

Введем понятие n-мерного координатного пространства Аⁿ

Def M-мерным координатным пространством А^m называется множетсво всевозможных упорядоченных совокупностей m действительных чисел (x1, x2, x3,…, xm)

Каждую упорядоченную совокупность (x1, x2,…,xm) называют точкой этого пространства и обозначают одной буквой М, при этом числа x1, x2, …,xn называются координатами точки М, что символически записывается так М( x1, x2,…xn)

Чтобы множество Х было метрическим пространством нужно:

Выберем в качестве множества Х n- мерное координатное пространство, возьмем люые х,у принадлежащие этому пространству. Х(х1…хn), y(y1..yn)

Введем функцию расстояния на Х между х и у. Р(х,у)=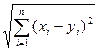

Линейное пространство L

Множество элементов L, содержащее хотя бы один элемент, называется линейным или векторным пространством, если выполнены следующие аксиомы:

1. Любые x,y принадлежат L, однозначно определен 3 элемент z, называемый их суммой, обозначаемый z=x+y, причем справедливые следующие свойства:

А) х+у=у+х (ассоциативность)

Б) (х+у)+z=x+(y+z)

В) Существует элемент (его обычно обозначают за 0) такой, что x+0=X

Г) Существует элемент Х, называемый противоположным, такой что x+x’=0

2) Для любого числа a и любого элемента х принадлежащего L определен элемент у из множества L= ax при этом справедливы следующие свойства:

a(b^х)=(ab)^х

(b+a)х=aх+bх

a(х+у)=aх+aу

1*x=x

х=х, где ab некоторые числа, х и у точка множества L. Если в аксиоме b и a принадлежат множеству вещественных чисел, то множества L называется действительным линейным пространством

Нормированное пространство N

Возьмем функция f(x)=||x||, ставящая каждому элементу х из множества L в соответствие вещественное число x принадлежащее L – называется нормой в линейном пространстве L, если выполнены следующие аксиомы:

1.f(x)=||x||=0 тогда и только тогда, когда х=0

2. f(aх)=|a|*||x||=|a|*f(x)

3. f(x+y)=||x+y||£||x|| +||y||=f(x)+f(y)

Пространство L, сведенное на этом множестве функцией норма X называют нормированным пространством и обозначают через N. ||x||>0

Следует отметить, что в любом норм. Пространстве может быть введена функция расстояния b(x,y)=||x*y|| как норма элемента х и у.

Def Координатное пространство Аⁿ называют n- мерным евклидовым пространством, если между двумя любыми точками х(х1, х2, …, хn) и у(у1, у2…уn) введена функция расстояния р(х,у) по формуле р(х,у)=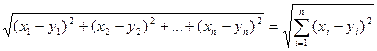

Обозначается n- мерное Евклидово пространство через Еⁿ

Следует отметить, что в этом пространстве могут быть ||x-y||=p(x,y)

Метрические пространства.

Будем говорить, что на множестве Х определена структура метрического пространства, если задана ф-я r(х,у) двух элементов х,уÎХ, удовлетворяющих следующим аксиомам:

1.r(х,у)=0 тогда и только тогда, когда х=у

2.r(х,у)=r(у,х) – аксиома симметрии

3.r(x,z)£r(x,y)+r(x,z)

Ф-я r(х,у) – метрика или ф-я расстояния между точками х,уÎХ.

Т.о. метрическое пространство R=(X,r): ф-я Х с введенной на этом множестве функцией метрикой.

r(х,х)£r(х,у)+r(у,х)

0£2r(х,у)

r(х,у)³0

Примеры:

1).X=R=E¹ (множество рациональных чисел)

r(х,у)=|х-у| - удовлетворяет условиям.

2). n-мерным пространством Аⁿ называют множество всевозможных упорядоченных совокупностей n вещественных чисел (х₁, х₂,…,х_n). Каждую упорядоченную совокупность называют точкой n-мерного пространства, а точки х₁, х₂,…,х_n – координатами точки. На Аⁿ, например, метрика:

n

r(х,у) = å((x_i-y_i)²)^1/2

i=1

Линейные пространства.

Множество элементов L, содержащее хотя бы 1 элемент называется линейным или векторным пространством, если выполнены следующие аксиомы:

1. Аксиомы сложения. Для любых двух элементов х,уÎL однозначно определен третий элемент z, называемый их суммой и обозначаемый z=x+y, и справедливы следующие свойства:

а)х+у = у+х

б)(x+y)+z = x+(y+z)

в)$ элемент, называемый нулевым и обозначаемый 0, такой, что для любых хÎL: х+0 = х

г) Для любого хÎХ $ элемент х¹, называемый противоположным, такой, что х+х¹ = 0

2. Аксиомы умножения на число. Для любого числа а и любого хÎL, определен элемент уÎL, называемый умножением числа а на элемент х и обозначаемый а*х, обладающий следующими свойствами (для любых чисел а, b и любых х,уÎL):

а) a(bx) = ab(x)

б) (a+b)x = ax+bx

в) a(x+y) = ax+ay

г) 1*x = 1

Замечание: если в аксиомах 2 a,bÎR, то линейное пространство называют действительным или вещественным линейным пространством.

Примеры:

1). А¹=R. В кач-ве операций сложения – сложение вещественных чисел; в кач-ве операций умножения – умножение вещественных чисел .

2). Aⁿ

1)а) z = x+y = (x₁+y₁, x₂+y₂,…,x_n+y_n) и так далее все свойства 1) и 2) групп по аналогии.

Нормированные пространства.

F(x) = ||x|| - “норма икс”, ставящая в соответствие любому хÎL (линейн. простран.) вещественное число ||х||, наз. нормой в лин. Пространстве, если она удовлетворяет следующим аксиомам:

1. ||х|| = 0 тогда и только тогда, когда х = 0

2. f(ax) = ||ax|| = ||a||*||x|| = |a|*f(x)

3. f(x+y) = ||x+y|| £ ||x||+||y|| = f(x)+f(y) (x,y - точки)

N – нормированное пространство.

||x||³0

В любом N может быть введена ф-я метрики r(x,y) = ||x-y|

Пример: А¹=R=L. F(x) = ||x||=|x| - удовлетворяет условиям.

n-мерное Евклидово пространство.

Координатное пространство Аⁿ называют n-мерным Евклидовым пространством и обозначают Еⁿ, если между двумя его точками ХÎЕⁿ и YÎЕⁿ введена ф-я расстояния r(х,у) по формуле:

n

||x|| = (å(x_i-y_i)²)^1/2

i=1

Еⁿ можно считать нормированным пространством, у которого

||x-y|| = r(x,y)