Равномерное и неравномерное квантование первичного сигнала
Как уже отмечалось, квантование отсчетных значений сигнала применяется для получения конечного числа разрешенных для передачи уровней отсчетов взамен непрерывного бесконечно большого количества их значений. С этой целью предполагаемый диапазон мгновенных напряжений сигнала разбивается на N отдельных интервалов - шагов квантования (рис.2).
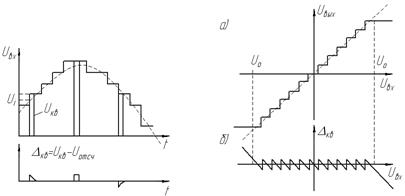
Рис.2. Амплитудное квантование непрерывного сигнала и вид амплитудной характеристики квантующего устройства (а) с временной функцией ошибки квантования (б).
Здесь Ui – среднее значение соседних разрешенных отсчетов; ∆i – i-й шаг квантования по напряжению. Если отсчетное значение напряжения сигнала удовлетворяет условию ui - ∆i /2 ≤ u ≤ ui + ∆i /2 , то ему присваивается значение i- го уровня квантования ui .
Квантование приводит к ошибке, которая может быть оценена разностью между истинным отсчетным значением напряжения сигнала и его квантованной величиной Ui : ∆квi = u - ui . В соответствии с рис. 1 полагаем, как это и делается на практике, что амплитудное квантование непрерывного сигнала производится после дискретизации сигнала. Амплитудная характеристика квантующего устройства (рис.1, а) представляется ступенчатой функцией, которая может быть выражена в виде суммы идеальной линейной характеристики и характеристики, определяющей искажения сигнала (рис.1, б). Характеристика uвых = φ (uвх) имеет два характерных участка: зону квантования и зону ограничения. Для первого участка --U0 ≤ uвх ≤ U0 и второго | uвх | > U0 . В соответствии с этим различают шумы квантования и шумы ограничения.
В системах с ИКМ определяющими являются шумы квантования. Ошибка квантования, как показано на рис.1,б является временной функцией с резкими скачками, частота которых гораздо больше частоты исходного сигнала и определяется количеством шагов квантования. Спектр ошибки квантования при передаче синусоидального сигнала будет дискретным и при передаче реального сигнала — шумоподобным. Этот спектр значительно шире спектра исходного сигнала; после дискретизации боковые спектры за счет ошибки квантования в области основной частоты дискретизации и ее гармоник будут перекрываться со спектром сигнала. Это позволяет оценить в первом приближении помеху от ошибки квантования мощностью (дисперсией) шумов квантования в спектре (0-0,5)fд. Дисперсию шумов квантования σ2кв выражают через вероятность pi попадания мгновенного напряжения сигнала в рассматриваемый интервал квантования: σ2квi = pi ∆2i /12. При равномерном квантовании, когда ∆i= const, принимается σ2квi = ∆2i /12.
Данная формула показывает, что при равномерном квантовании дисперсия (мощность) шумов квантования σ2кв (Ркв) определяется лишь шагом квантования и не зависит от уровня сигнала. При заданном динамическом диапазоне сигнала величина ∆ определяет число уровней квантования и, следовательно, число разрядов кода m, необходимого для последующего кодирования квантованных отсчетов сигнала. Для определения требуемого числа разрядов кода необходимо определить защищенность (aкв.) сигнала от шума квантования.
При пороге ограничения Uo величина шага ∆ равномерного квантования в зависимости от числа разрядов кода m должна быть равна: ∆=Uo /2m-1 при передаче двуполярных сигналов и при передаче однополярных сигналов ∆= Uo /2m , т.к. возможное число кодируемых уровней напряжения соответственно равно 2m-1 и 2m. Тогда при передаче синусоидального сигнала с амплитудой Um, когда его средняя мощность на сопротивлении в 1 Ом равна Pc=U2m/2, защищенность сигнала от шума квантования будет равна aкв.=10 lg(12Pc/∆2) дБ. Подставляя значения Pc и ∆ определяем aкв.=6m+1,8+20lg Um/ Uo .
Данная формула показывает, что величина aкв. при равномерном квантовании увеличивается на 6 дБ с увеличением числа разрядов кода на каждую единицу и при Um<U0 она растет прямо пропорционально уровню сигнала в децибелах. Если Um=U0, то величина aкв при данном значении m будет максимальной и равной aкв.=6m+1,8.
Найдем теперь величину aкв. при передаче речевого сигнала. Известно, что уровень средней мощности речевых сигналов подчиняется нормальному закону распределения со средним значением p0 = - 13,6 дБ и стандартным отклонением σ =5 дБ. Допуская превышение уровня средней мощности в активном канале с вероятностью не более 10-3 для максимального и минимального его значений, получим рмакс= p0 + 3,1σ , рмин= p0 + 3,1σ . если учесть пикфактор речевого сигнала v=12 дБ, то пиковое значение уровня с той же вероятностью 10-3 будет равно рпик = рмакс+12 = p0 + 3,1σ +12 дБ.
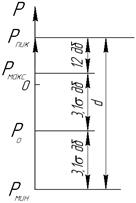 Рис. 3. Динамический диапазон речевого сигнала Рис. 3. Динамический диапазон речевого сигнала | Следовательно, динамический диапазон речевого сигнала, с вероятностью которого необходимо считаться (рис.3), составит d = рпик - рмин = 6,2 σ +12=43 дБ. Если теперь выбрать порог ограничения U0 в соответствии с величиной рпик ,то требуемое число m будет равно m=( aкв. + 43 – 1,8)/6. Обычно требуют, чтобы величина aкв. при минимальном уровне средней мощности речевого сигнала была не менее 20 дБ. При максимальном количестве переприемов по тональной частоте, предусматриваемом в перспективных сетях связи и равном 10, указанную величину aкв. для одного переприемного участка следует увеличить на 10lg11 = 10,4 дБ и поэтому в качестве расчетной для одного переприемного участка следует принять величину aкв. = 20+10,4 = = 30,4 дБ. При этом требуемое число разрядов кода будет равно m= 12. |
Как видно, при равномерном квантовании для получения требуемой защищенности от шумов квантования при передаче речевых сигналов кодирование должно производиться при достаточно большом числе разрядов кода, что нежелательно. Ведь с увеличением числа разрядов кода уменьшается длительность импульсов в кодовой группе, соответственно расширяется спектр сигнала ИКМ, усложняются устройства кодирования и декодирования и увеличиваются требования к их быстродействию. Кроме того, в случае применения симметричных двоичных кодов могут возникать «шумы молчания» с амплитудой напряжения ∆/2. Дисперсия этого шума равна ∆2/4 и, следовательно, мощность шумов молчания Рш.м. будет в 3 раза больше величины Ркв . Необходимое число разрядов кода m при передаче речевых сигналов в системе с ИКМ можно заметно уменьшить, если применить неравномерное квантование, когда шаг квантования невелик для слабых сигналов и увеличивается по мере возрастания уровня сигнала. При неравномерном квантовании, когда шаг квантования в центральной зоне амплитудной характеристики имеет минимальное значение, величина Рш.м. существенно уменьшается и становится гораздо меньше мощности шумов квантования Ркв .
При равномерном квантовании защищенность от шумов квантования aкв. минимальна для наиболее слабых сигналов и увеличивается прямо пропорционально увеличению уровня сигнала. Для выравнивания величины aкв. в широких пределах применяют неравномерное квантование, которое имеет нелинейную шкалу квантования.
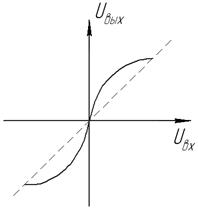
Нелинейная шкала квантования в системах передачи с ИКМ может быть реализована следующими способами: сжатием динамического диапазона сигнала перед кодированием с линейной шкалой квантования и последующим его расширением после декодирования компандерами мгновенного действия; нелинейным кодированием и декодированием; цифровым компандированием. Все три способа практически равноценны в отношении возможностей выравнивания защищенности от шумов квантования для заданного динамического диапазона сигнала. Однако они отличаются не только схемными решениями, объемом оборудования, но и эксплуатационными характеристиками. Так, нелинейные кодеки и цифровые компандеры обеспечивают лучшую стабильность характеристик канала. Им не свойственны недостатки, имеющие место при несогласованной работе компрессора и экспандера. Амплитудная характеристика компрессора uвых = φ(uвх) показана на рис.4. Шаг квантования в зависимости от величины uвх определяется крутизной амплитудной характеристики. При неравномерном квантовании применяют компрессоры с амплитудной характеристикой вида: y=[ln(1+μ| uвх | / U0)] / ln(1+ μ).
 |  |
а) б)
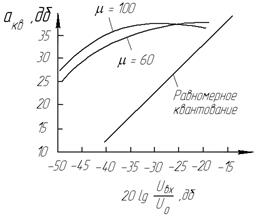
Рис. 4. Амплитудная характеристика компрессора (а) и зависимость aкв. от уровня сигнала для различных μ (б).
При μ =100 - 250 выигрыш в помехозащищенности для слабых сигналов за счет неравномерного квантования составляет ∆aкв. = 26—33 дБ. Увеличение величины aкв. на 26 дБ при неравномерном квантовании позволяет уменьшить число разрядов кода на 26:6 = 4 и, следовательно, обеспечить требуемую защищенность от шумов квантования для наиболее слабых речевых сигналов при 8-разрядном кодировании вместо 12-разрядного кодирования при равномерном квантовании. Такое число разрядов кода соответствует рекомендациям МККТТ для современных систем ИКМ с учетом переприемов по ТЧ.
Поскольку разница между уровнями сигнала и шума (защищенность от шума квантования) величина логарифмическая, все реализации компрессии имеют характеристику, близкую к логарифмической. Наряду с логарифмическими характеристиками компрессии типа μ, в системах с ИКМ наибольшее распространение получила 16-сегментная шкала квантования с характеристикой компрессии, соответствующей А-закону (рис.5).
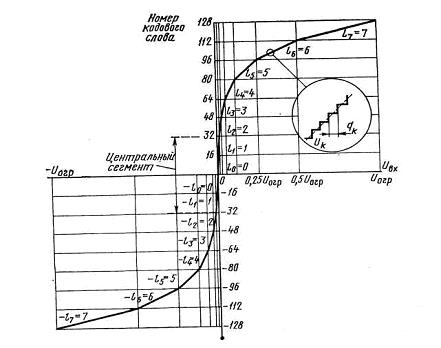
Рис. 5. Логарифмическая характеристика компрессии по закону А.
В этом случае весь динамический диапазон делят на 16 сегментов, по восемь для каждой полярности. В пределах каждого сегмента шаг квантования неизменен. Для сигналов, абсолютная величина которых не превышает 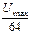 , шаг квантования равномерный, в дальнейшем шаг удваивается в каждом следующем сегменте. Эта амплитудная характеристика является линейно-ломанной, основанной на 16-сегментной аппроксимации.
, шаг квантования равномерный, в дальнейшем шаг удваивается в каждом следующем сегменте. Эта амплитудная характеристика является линейно-ломанной, основанной на 16-сегментной аппроксимации.
Сегменты 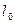 ,
, 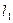 ,
, 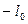 ,
, 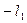 имеют одинаковый наклон, следовательно, их считают единичным сегментом, следовательно, характеристика компрессора получается 13-сегментной. В пределах каждого сегмента размещается 16 шагов квантования
имеют одинаковый наклон, следовательно, их считают единичным сегментом, следовательно, характеристика компрессора получается 13-сегментной. В пределах каждого сегмента размещается 16 шагов квантования 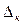 (к = 0,1,…,15).
(к = 0,1,…,15).
При 8-разрядном нелинейном кодировании первый разряд несёт информацию о полярности отсчёта входного сигнала. Следующие три разряда кода образуют номер сегмента ( 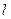 = 0, 1, 2,…,7), а последние четыре разряда – образуют номер шага квантования (
= 0, 1, 2,…,7), а последние четыре разряда – образуют номер шага квантования ( 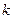 = 0, 1,…,15) в пределах сегмента.
= 0, 1,…,15) в пределах сегмента.
таблица 6
| Номер сегмента. | Размер шага квантования. | Верхняя граница сегмента |
64 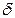 | 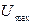 (порог перегрузки) (порог перегрузки) | |
32 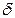 | 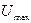 /2 /2 | |
16 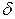 | 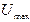 /4 /4 | |
8 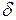 | 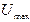 / 8 / 8 | |
4 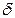 | 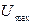 /16 /16 | |
2 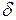 | 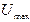 /32 /32 | |
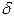 | 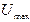 /64 /64 | |
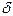 | 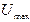 /128 /128 |
Амплитудная характеристика компандирования описывается выражениями:
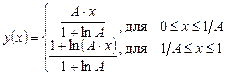
где х = uвх/U0, А = 87.6 – параметр компрессии.
Максимально-допустимая величина защищенности от шумов квантования для амплитудной характеристики квантующего устройства может быть определена по формуле:
aкв. = 6m+1,8+∆aкв. – C. С – коэффициент компандирования.
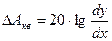 ;
; 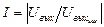 - нормированное
- нормированное 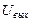
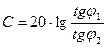 ;
; 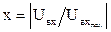 - нормированное
- нормированное 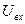
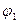 – угол наклона первого сегмента,
– угол наклона первого сегмента, 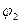 – угол наклона последнего сегмента характеристики квантующего устройства.
– угол наклона последнего сегмента характеристики квантующего устройства.
Величина 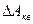 для 13-сегментной характеристики компандирования
для 13-сегментной характеристики компандирования 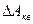 = 24 dB, а коэффициент компрессии С = 36 dB.
= 24 dB, а коэффициент компрессии С = 36 dB.
Тогда:
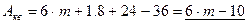 .
.
Определение разрядности кодовой комбинации необходимо для обеспечения защищенности от шумов квантования и выбора равномерного (линейного) или неравномерного (нелинейного) квантования. При проектировании следует дать сравнительный анализ равномерного и неравномерного квантования, обоснование применения неравномерного квантования с амплитудной характеристикой квантующего устройства сигналов АИМ-II, близкой к логарифмической.
Амплитудная характеристика у = f(x) реализуется в виде каскадного соединения компрессора с указанной амплитудной характеристикой, АЦП с равномерной шкалой квантования и порогом перегрузки равным Uorp = Uвх max .
Необходимую защищенность от шумов квантования в системе ИКМ обеспечивают оба вида характеристик компрессии. Так, на рис. 6 для сравнения приведена зависимость величины aкв. от уровня входного сигнала uвх/U0 при μ = 255 и А = 87,6/13.
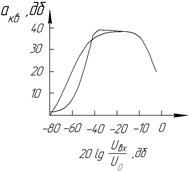
Рис.6. Зависимость величины защищенности aкв. от uвх/U0 при μ = 255 и А = 87,6.
- Примеры выбора частоты дискретизации сигналов.
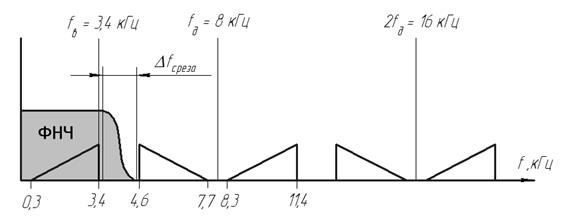
Рис.7. Спектральная диаграмма АИМ-сигнала.
Минимальное значение Fд должно обеспечивать неискажённое восстановление первичного сигнала с учётом не идеальности фильтров, которые включаются на входе канальных АИМ и на выходе канального селектора.
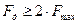 ,
,
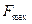 - максимальное значение верхней граничной частоты первичного сигнала С(t). Данное соотношение справедливо для первичных сигналов, у которых отношение граничных частот превышает несколько октав:
- максимальное значение верхней граничной частоты первичного сигнала С(t). Данное соотношение справедливо для первичных сигналов, у которых отношение граничных частот превышает несколько октав:
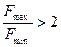 ,
,
Здесь 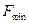 - минимальное значение нижней граничной частоты непрерывного во времени первичного сигнала С(t). При этом, в ЦСП дискретизации подвергаются не только первичные сигналы, а также групповые сигналы, соответствующие сигналам первичного широкополосного канала, для которого Fmin = 60 кГц, Fmax = 108 кГц или сигналам вторичного широкополосного канала (Fmin = 312 кГц, Fmax = 552 кГц) и т.д. для этих сигналов отношениие граничных частот всегда меньше двух. В этом случае частота дискретизации определяется из соотношений:
- минимальное значение нижней граничной частоты непрерывного во времени первичного сигнала С(t). При этом, в ЦСП дискретизации подвергаются не только первичные сигналы, а также групповые сигналы, соответствующие сигналам первичного широкополосного канала, для которого Fmin = 60 кГц, Fmax = 108 кГц или сигналам вторичного широкополосного канала (Fmin = 312 кГц, Fmax = 552 кГц) и т.д. для этих сигналов отношениие граничных частот всегда меньше двух. В этом случае частота дискретизации определяется из соотношений:
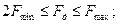
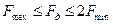 .
.
Физической реализацией процесса дискретизации является АИМ, при которой амплитудной модуляции подвергаются импульсы, следующие с частотой Fд или периодом дискретизации Тд = 1/ Fд. Если вершина амплитуды отсчета соответствует исходному сигналу, т.е. повторяет форму исходного сигнала на длительности отсчета τи ,то такая АИМ называется амплитудно-импульсной модуляцией первого рода (АИМ-I), если вершина амплитуды отсчета на всей его длительности τи остается величиной постоянной, то такая АИМ называется АИМ второго рода (АИМ-II).
При скважности периодической, модулируемой последовательности импульсов 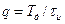 (где Тд - период дискретизации - период следования импульсов модулируемой последовательности, τи - длительность импульсов этой последовательности) более десяти, существенного отличия между АИМ-1 и АИМ-П нет и можно считать, что их спектры одинаковы. Спектр АИМ однополярной последовательности включает: постоянную составляющую, исходный сигнал, гармоники частоты дискретизации, верхние и нижние боковые полосы около этих гармоник, т.е. полоса n
(где Тд - период дискретизации - период следования импульсов модулируемой последовательности, τи - длительность импульсов этой последовательности) более десяти, существенного отличия между АИМ-1 и АИМ-П нет и можно считать, что их спектры одинаковы. Спектр АИМ однополярной последовательности включает: постоянную составляющую, исходный сигнал, гармоники частоты дискретизации, верхние и нижние боковые полосы около этих гармоник, т.е. полоса n 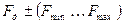 .
.
Пример 1. Определить минимальное значение 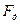 сигнала вещания первого класса с полосой
сигнала вещания первого класса с полосой 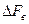 =0,05…10 кГц, при котором будут отсутствовать искажения дискретизации. Частотные характеристики фильтров ФНЧ на входе канального АИМ и выходе канального селектора считать идеальными. Представить графически частотный спектр АИМ сигнала.
=0,05…10 кГц, при котором будут отсутствовать искажения дискретизации. Частотные характеристики фильтров ФНЧ на входе канального АИМ и выходе канального селектора считать идеальными. Представить графически частотный спектр АИМ сигнала.
Решение. Из условия ясно, что Fmin = 0,05 кГц, Fmax = 10 кГц. Минимальное значение частоты дискретизации 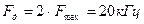 . Спектр АИМ сигнала SАИМ (f) приведен на рис.8.
. Спектр АИМ сигнала SАИМ (f) приведен на рис.8.
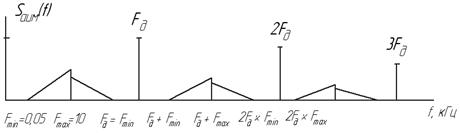
Рис.8. спектр АИМ сигнала.
Пример 2. Определить минимальное значение частоты дискретизации 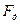 сигнала вещания высшего класса с полосой
сигнала вещания высшего класса с полосой 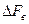 =0,03…15 кГц, при котором будут отсутствовать искажения дискретизации. Частотные характеристики фильтров ФНЧ на входе КАИМ и выходе КС реальные. ∆Fр = 2 кГц – ширина полосы расфильтровки между исходным сигналом и нижней боковой полосы частот первой гармоники частоты дискретизации.
=0,03…15 кГц, при котором будут отсутствовать искажения дискретизации. Частотные характеристики фильтров ФНЧ на входе КАИМ и выходе КС реальные. ∆Fр = 2 кГц – ширина полосы расфильтровки между исходным сигналом и нижней боковой полосы частот первой гармоники частоты дискретизации.
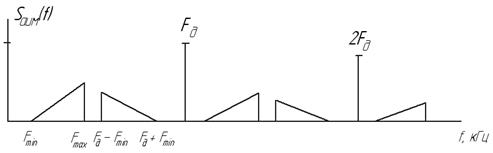
Рис.9. Спектр АИМ сигнала.
Решение. Из рис.9 следует: 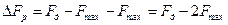 . Следовательно, частота дискретизации при использовании фильтров с реальными характеристиками всегда определяется го соотношения:
. Следовательно, частота дискретизации при использовании фильтров с реальными характеристиками всегда определяется го соотношения: 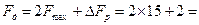 32 кГц.
32 кГц.
Ширина полосы расфильтровки определяется требованиями к величине подавления ненужных спектральных составляющих АИМ сигнала при его демодуляции и крутизной характеристики затухания фильтра в полосе расфильтровки.
Пример 3. Определить минимальное значение частоты дискретизации сигнала первичного широкополосного канала, дня которого 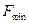 = 60 кГц и
= 60 кГц и 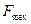 = 108 кГц, обеспечивающее отсутствие искажений дискретизации при демодуляции АИМ сигнала. Принять частотные характеристики затухания полосовых фильтров на входе КАИМ и выходе КС идеальными.
= 108 кГц, обеспечивающее отсутствие искажений дискретизации при демодуляции АИМ сигнала. Принять частотные характеристики затухания полосовых фильтров на входе КАИМ и выходе КС идеальными.
Решение. Из соотношений 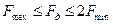 следует, что частоты дискретизации сигнала первичного широкополосного канала должны удовлетворять условиям: 108
следует, что частоты дискретизации сигнала первичного широкополосного канала должны удовлетворять условиям: 108 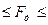 120 кГц. Исходя из условий задачи выбираем
120 кГц. Исходя из условий задачи выбираем  = 108 кГц. Спектр АИМ сигнала для: этого примера приведен на рис.10, где приняты следующие обозначения: НБ-1 нижняя, боковая полоса от первой гармоники частоты дискретизации; ВБ-1 верхняя боковая полоса частот от первой гармоники частоты дискретизации; НБ-2 и ВБ-2 аналогично нижняя и верхняя боковая полоса частот от второй гармоники частоты дискретизации.
= 108 кГц. Спектр АИМ сигнала для: этого примера приведен на рис.10, где приняты следующие обозначения: НБ-1 нижняя, боковая полоса от первой гармоники частоты дискретизации; ВБ-1 верхняя боковая полоса частот от первой гармоники частоты дискретизации; НБ-2 и ВБ-2 аналогично нижняя и верхняя боковая полоса частот от второй гармоники частоты дискретизации.
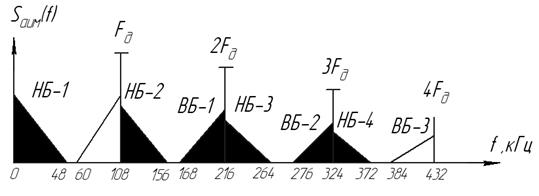
Рис.10. Пример спектра АИМ сигнала.
В практике проектирования АИМ трактов ЦСП на выбор частоты дискретизации влияет на возможность технической реализации фильтров нижних частот (ФНЧ) или полосовых фильтров на входе КАИМ и выходе КС.
Реализация этих фильтров определяется величиной защитного интервала или полосой расфильтровки 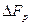 между полосой частот исходного сигнала
между полосой частот исходного сигнала 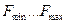 и боковыми полосами частот вокруг гармоник частоты дискретизации. Величина этого защитного интервала или полосы расфильтровки определяется возможностями реализации фильтров с реальной крутизной характеристики затухания в переходной области или в полосе расфильтровки, (рис.11), где приняты следующие обозначения:
и боковыми полосами частот вокруг гармоник частоты дискретизации. Величина этого защитного интервала или полосы расфильтровки определяется возможностями реализации фильтров с реальной крутизной характеристики затухания в переходной области или в полосе расфильтровки, (рис.11), где приняты следующие обозначения:  - полоса расфильтровки или защитный интервал, или переходная область, т.е. переход от полосы эффективного пропускания (ПЭП) к полосе эффективного задерживания (ПЭЗ),
- полоса расфильтровки или защитный интервал, или переходная область, т.е. переход от полосы эффективного пропускания (ПЭП) к полосе эффективного задерживания (ПЭЗ),  - минимально-допустимое затухание в ПЭЗ, обеспечивающее достаточное подавление побочных продуктов преобразования - дискретизации (амплитудно-импульсной модуляции), исключающее искажения дискретизации.
- минимально-допустимое затухание в ПЭЗ, обеспечивающее достаточное подавление побочных продуктов преобразования - дискретизации (амплитудно-импульсной модуляции), исключающее искажения дискретизации.
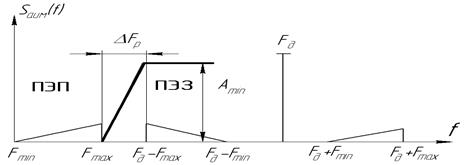
Рис.11. Определение полосы расфильтровки.
Пример 4. Определить частоту дискретизации телефонного сигнала с 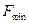 = 300 Гц и
= 300 Гц и 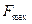 = 3400 Гц, при которой будут отсутствовать искажения дискретизации, если на входе КАИМ и на выходе КС включается ФНЧ с шириной полосы расфильтровки - защитного интервала
= 3400 Гц, при которой будут отсутствовать искажения дискретизации, если на входе КАИМ и на выходе КС включается ФНЧ с шириной полосы расфильтровки - защитного интервала 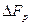 = 1200 Гц.
= 1200 Гц.
Решение. Известно, что 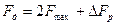 .Подставляя значения
.Подставляя значения 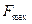 и
и 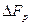 , получим
, получим 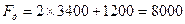 Гц.
Гц.
По-иному определяется значение частоты дискретизации 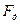 для узкополосных сигналов, для которых отношение
для узкополосных сигналов, для которых отношение 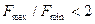 . При наличии защитных интервалов спектр АИМ сигнала для этого случая может быть представлен в виде, рис.12. Принятые обозначения очевидны, они были указаны ранее.
. При наличии защитных интервалов спектр АИМ сигнала для этого случая может быть представлен в виде, рис.12. Принятые обозначения очевидны, они были указаны ранее.
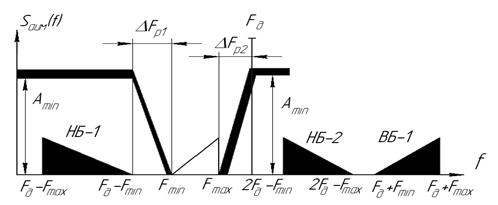
Рис.12. К определению полос расфильтровки.
Из рис.12 следует, что 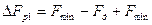 , т.е.
, т.е. 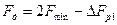 .
.
С другой стороны из рисунка следует, что 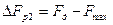 .
.
Соответственно, для частоты дискретизации имеем следующее выражение 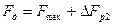 .
.
Пример 5. Определить минимальное значение 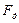 вторичного широкополосного канала с
вторичного широкополосного канала с 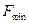 = 312 кГц и
= 312 кГц и 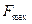 = 552 кГц, которая обеспечивает отсутствие искажений дискретизации при демодуляции сигнала, если
= 552 кГц, которая обеспечивает отсутствие искажений дискретизации при демодуляции сигнала, если 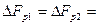 12 кГц.
12 кГц.
Решение. Из рис.12 получим:
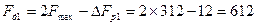 кГц
кГц
Из 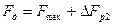 следует, что
следует, что 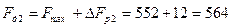 кГц.
кГц.
Из двух значений выбираем меньшее, т.е. 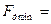 564 кГц.
564 кГц.
Из полученных значений частоты дискретизации и на основании рис.12 определим значения полос расфильтровки:
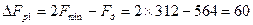 кГц;
кГц;
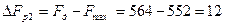 кГц.
кГц.
Таким образом, для полосовых фильтров, включаемых на входе КАИМ и на выходе КС, получаются асимметричные характеристика затухания (рис.13).
Следовательно, выбор частоты дискретизации сигналов электросвязи зависит от двух факторов: широкополосности сигнала, т.е. отношения 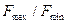 , и возможности реализации фильтров с требуемым значением
, и возможности реализации фильтров с требуемым значением 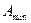 и возможно достижимой крутизны частотной характеристики затухания фильтра, т.е.
и возможно достижимой крутизны частотной характеристики затухания фильтра, т.е. 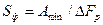 . Естественно, стремление к получению минимально возможного значения частоты дискретизации.
. Естественно, стремление к получению минимально возможного значения частоты дискретизации.
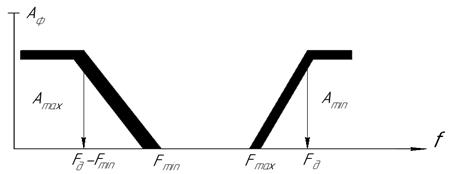
Рис.13. Характеристика затухания фильтров.
Следовательно, частота дискретизации должна выбираться для сигналов равной (2,3…2,4) 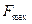 и соответствующей стандартной частоте дискретизации аналого-цифрового оборудования типовых первичных систем передачи.
и соответствующей стандартной частоте дискретизации аналого-цифрового оборудования типовых первичных систем передачи.
Полосу расфильтровки фильтров нижних частот следует выбирать равной 1,2...2,0 кГц для первичных сигналов телефонных, радиовещательных сообщений. Что касается дискретизации сигналов с отношением Fmax / Fmin меньше двух, то частоту дискретизации следует выбирать согласно вышеприведенным формулам, а полосу расфильтровки фильтров следует брать в пределах от 8 до 60 кГц, в зависимости от широкополосности сигналов такого типа.
