Линейные операции над векторами
ВЫСШАЯ МАТЕМАТИКА
ВЕКТОРНАЯ АЛГЕБРА.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Методические указания и примеры
решения типовых задач для студентов
I курса очной формы обучения
инженерно – технических направлений
(I семестр)
Брянск 2012
УДК 511
Высшая математика. Векторная алгебра. Аналитическая геометрия. [Текс]+[Электронный ресурс]: методические указания и примеры решения типовых задач для студентов I курса очной формы обучения инженерно – технических направлений (I семестр). – Брянск: БГТУ, 2012. – 36с.
Разработали: Н.А.Ольшевская, доц.
Г.Г. Цуленева, доц.
К.А. Сенько, асс.
Рекомендовано кафедрой «Высшая математика» БГТУ
(протокол № 5 от 31.01.12)
СОДЕРЖАНИЕ
Векторная алгебра
1.1. Векторы. Основные понятия.
Линейные операции над векторами…………………………….….4
1.2. Скалярное произведение двух векторов..……………………………6
1.3. Векторное произведение двух векторов…………………………….8
1.4. Смешанное произведение трех векторов……………………..……10
1.5. Задачи для самостоятельного решения…………………………….12
Аналитическая геометрия
2.1. Прямая линия на плоскости…………………………………………13
2.2. Кривые второго порядка на плоскости……………………..………19
2.3. Плоскость в пространстве………………………………….…..……24
2.4. Прямая в пространстве. Прямая и плоскость…………….…..…….27
2.5. Задачи для самостоятельного решения……………………..………34
Список рекомендуемой литературы……………………………………..……..35
ВЕКТОРНАЯ АЛГЕБРА
Векторы. Основные понятия.
Линейные операции над векторами
Геометрический вектор 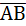 – это направленный отрезок, у которого один конец (точка А) называется началом вектора, а другой конец (точка В) – концом вектора.
– это направленный отрезок, у которого один конец (точка А) называется началом вектора, а другой конец (точка В) – концом вектора.
Длиной вектора (модулем) называют длину отрезка АВ. Векторы обозначают как 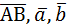 , а их длины
, а их длины 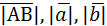 .
.
Два вектора называются равными, если они имеют равные длины и одинаковое направление.
Вектор, начало и конец которого совпадают, называется нулевым.
Произведением вектора 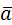 на некоторое число αÎR называется вектор, длина которого равна длине вектора
на некоторое число αÎR называется вектор, длина которого равна длине вектора 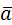 , умноженной на абсолютную величину числа α, а направление совпадает с направлением вектора
, умноженной на абсолютную величину числа α, а направление совпадает с направлением вектора 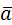 , если α>0, и противоположно ему, если α<0.
, если α>0, и противоположно ему, если α<0.
Суммой нескольких векторов называется вектор, проведенный из начала первого вектора в конец последнего при условии, что начало каждого последующего вектора совмещается с концом предыдущего.
Проекцией вектора 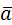 на ось Ох называется число, равное длине вектора
на ось Ох называется число, равное длине вектора 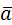 , умноженной на косинус угла между вектором
, умноженной на косинус угла между вектором 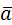 и положительным направлением оси Ох.
и положительным направлением оси Ох.
Радиусом-вектором точки М называется вектор 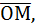 соединяющий начало координат с этой точкой.
соединяющий начало координат с этой точкой.
Единичные векторы координатных осей 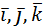 называются ортами.
называются ортами.
Углы α, β, γ между вектором 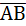 и положительными направлениями осей координат называются направляющими, при этом для вектора
и положительными направлениями осей координат называются направляющими, при этом для вектора 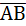 с координатами Х, Y, Z
с координатами Х, Y, Z
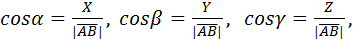 причем
причем 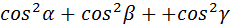 =1.
=1.
Если векторы 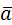 и
и 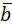 заданы своими координатами как
заданы своими координатами как 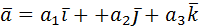 и
и 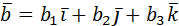 , то координаты вектора
, то координаты вектора 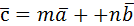 будут равны: {ma1 +nb1, ma2+nb2, ma3+nb3}, а вектор
будут равны: {ma1 +nb1, ma2+nb2, ma3+nb3}, а вектор 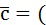 ma1 +nb1)
ma1 +nb1) 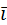 +(ma2+nb2)
+(ma2+nb2) 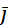 +(ma3+nb3)
+(ma3+nb3) 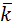 .
.
Примеры решения типовых задач
1. Найти длину вектора 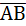 , если А(1;2;3); В(2;-5;4).
, если А(1;2;3); В(2;-5;4).
Решение:
Найдем координаты вектора 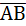 :
: 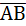 {2-1;-5-2;4-3}; АВ{1;-7;1}.
{2-1;-5-2;4-3}; АВ{1;-7;1}.
Найдем длину вектора 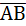 :
:
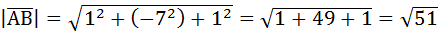 .
.
Ответ: 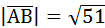 .
.
2. Найти длину радиус-вектора точки А(2;3;-1).
Решение:
Координаты радиус-вектора точки А совпадают с координатами самой точки: 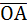 {2;3;-1}.
{2;3;-1}.
Найдем длину радиус-вектора 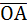 :
:
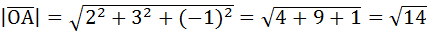 .
.
Ответ: 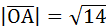 .
.
3. Найти длину вектора 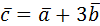 , если
, если 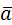 {1;-1;0},
{1;-1;0}, 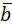 {3;-1;4}.
{3;-1;4}.
Решение:
Найдем координаты вектора 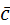 :
: 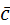 {1+3∙3;-1+3(-1);0+3∙4};
{1+3∙3;-1+3(-1);0+3∙4}; 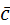 {10;-4;12}.
{10;-4;12}.
Найдем длину вектора 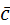 :
:
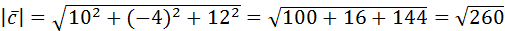 .
.
Ответ: 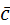 =
= 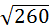 .
.
4. Найти направляющие косинусы вектора 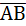 , если А(1;-1;3), В(2;-3;4).
, если А(1;-1;3), В(2;-3;4).
Решение:
Найдем координаты вектора 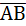 :
: 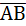 {2-1;-3-(-1);4-3},
{2-1;-3-(-1);4-3}, 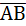 {1;-2;1}.
{1;-2;1}.
Найдем длину вектора 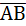 :
:
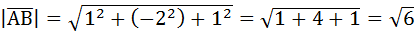 .
.
Итак, 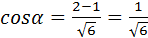 ;
; 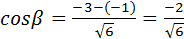 ;
; 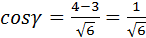 .
.
Проверка: 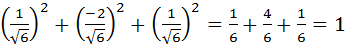 .
.
Ответ: 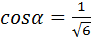 ;
; 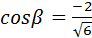 ;
; 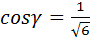 .
.
Примеры решения типовых задач
1. Даны векторы 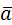 =3
=3 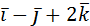 и
и 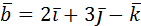 . Найти: а)
. Найти: а) 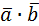 ;
;
б) 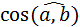 ; в)
; в) 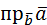 .
.
Решение:
а) 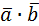 =3∙2+(-1)3+2(-1)=6-3-2=1;
=3∙2+(-1)3+2(-1)=6-3-2=1;
б) 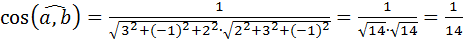 ;
;
в) 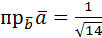 .
.
Ответ: а) 1; б)  ; в)
; в) 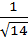 .
.
2. Даны векторы 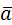 {3;-1;4},
{3;-1;4}, 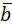 {-2;2;2}. Проверить, являются ли они ортогональными.
{-2;2;2}. Проверить, являются ли они ортогональными.
Решение:
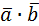 =3∙(-2)+(-1)2+4∙2=-6-2+8=0. Следовательно, векторы
=3∙(-2)+(-1)2+4∙2=-6-2+8=0. Следовательно, векторы 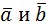 ортогональны.
ортогональны.
3. Вычислить работу силы 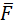 ={3;2;4}, если точка ее приложения перемещается прямолинейно из положения А(2;4;6) в положение В(4;2;7).
={3;2;4}, если точка ее приложения перемещается прямолинейно из положения А(2;4;6) в положение В(4;2;7).
Решение:
А= 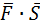 . Найдем координаты вектора
. Найдем координаты вектора 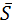 =
= 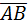 :
:
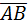 {4-2;2-4;7-6};
{4-2;2-4;7-6};
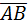 ={2;-2;1}.
={2;-2;1}.
Найдем работу А:
А=3∙2+2(-2)+4∙1=6-4+4=6.
Ответ: 6.
4. Найти длины диагоналей параллелограмма (рис.1), построенного на векторах 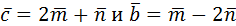 , где
, где 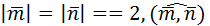 =60˚.
=60˚.
 |
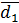 |
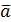
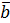 |
| Рис.1 |
Решение:
Выразим диагонали параллелограмма 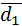 и
и 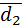 по правилу
по правилу
параллелограмма: 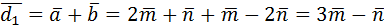 ,
,
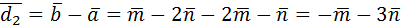 .
.
Так как векторы 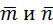 не единичные, следовательно,
не единичные, следовательно, 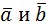 заданы в произвольном базисе, то
заданы в произвольном базисе, то 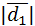 и
и 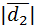 можно найти по определению:
можно найти по определению:
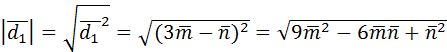 =
=
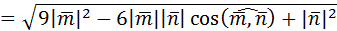 =
= 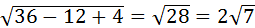 .
.
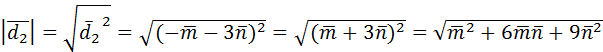 =
=
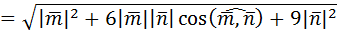 =
= 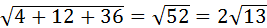 .
.
Ответ: 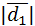 =
= 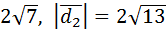 .
.
Примеры решения типовых задач
1. Раскрыть скобки и упростить выражение:
а)  ;
;
б) (2 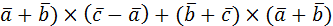 .
.
Решение:
а) 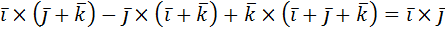 +
+ 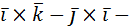
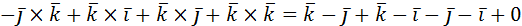 =2
=2 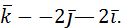
б) (2 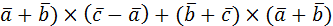 =2
=2 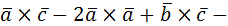
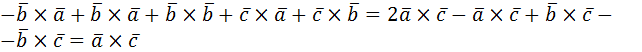 .
.
2. Даны векторы 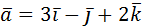 и
и 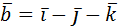 . Найти
. Найти 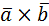 .
.
Решение:
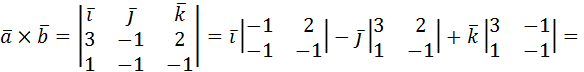
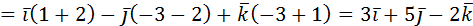 .
.
Ответ: 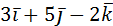 .
.
3. Найти площадь ∆АВС, если А(1;2;0); В(3;0;-3); С(5;2;6).
Решение:
S∆АВС= 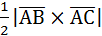 . Найдем координаты векторов
. Найдем координаты векторов 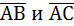 :
:
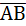 {3-1;0-2;-3-0}={2;-2;-3};
{3-1;0-2;-3-0}={2;-2;-3};
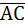 {5-1;2-2;6-0}={4;0;6}.
{5-1;2-2;6-0}={4;0;6}.
Найдем векторное произведение 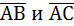 :
:
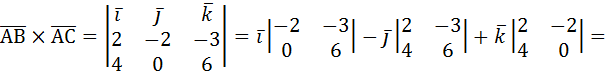
= 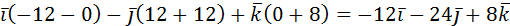 .
.
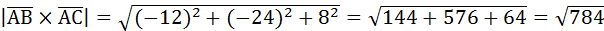 .
.
S∆АВС= 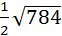 .
.
Ответ: 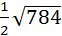 .
.
4. Сила 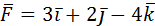 приложена в точке М(2;-1;1). Найти ее
приложена в точке М(2;-1;1). Найти ее
момент относительно начала координат.
Решение:
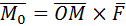 . Найдем координаты вектора
. Найдем координаты вектора 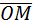 : О(0;0;0), М(2;-1;1), следовательно,
: О(0;0;0), М(2;-1;1), следовательно, 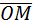 {2;-1;1}.
{2;-1;1}.
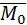 =
= 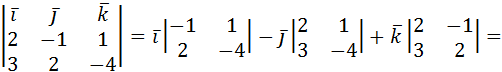
= 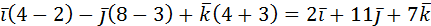 .
.
Ответ: 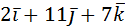 .
.
Примеры решения типовых задач
1. Найти объем пирамиды, вершинами которой служат точки
А(1;2;3); В(0;-1;1); С(2;5;2); D(3;0;-2).
Решение:
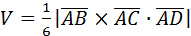 . Найдем координаты векторов
. Найдем координаты векторов 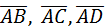 :
:
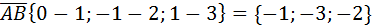 ;
;
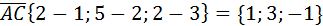 ;
;
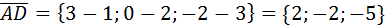 .
.
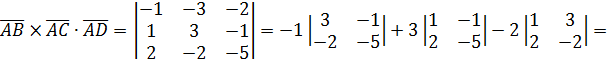
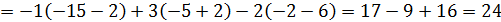 .
.
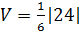 =4.
=4.
Ответ: 4.
2. Доказать, что векторы 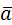 =2
=2 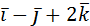 ,
, 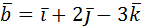 и
и 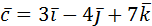 компланарны.
компланарны.
Доказательство:
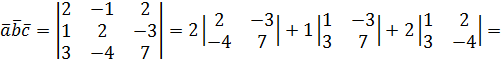
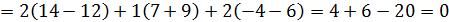 ,следовательно,
,следовательно, 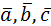 компланарны.
компланарны.
3. Проверить, лежат ли точки А(2;-1;-2), В(1;2;1), С(2;3;0), D(5;0;6) в одной плоскости.
Решение:
Для того чтобы доказать, что точки А, В, С, D лежат в одной плоскости, нужно доказать, что векторы 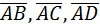 компланарны. Найдем координаты векторов
компланарны. Найдем координаты векторов 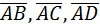 :
:
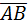 {1-2;2-(-1);1-(-2)}={-1;3;3};
{1-2;2-(-1);1-(-2)}={-1;3;3};
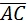 {2-2;3-(-1);0-(-2)}={0;4;2};
{2-2;3-(-1);0-(-2)}={0;4;2};
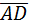 {5-2;0-(-1);6-(-2)}={3;1;8}.
{5-2;0-(-1);6-(-2)}={3;1;8}.
Проверим компланарность векторов 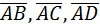 :
:
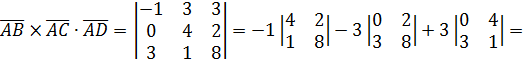
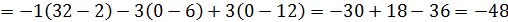 , следовательно, векторы
, следовательно, векторы 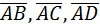 не компланарны, таким образом, точки А, В, С, D не лежат в одной плоскости.
не компланарны, таким образом, точки А, В, С, D не лежат в одной плоскости.
4. Даны координаты вершин пирамиды А(1;2;-3), В(1;0;-1), С(2;4; -6), D(0;-1;3). Найти а) VАВСD; б) S∆АВС; в) 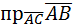 ; г)
; г) 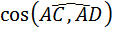 .
.
Решение:
а)VАВСD= 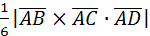 . Найдем координаты векторов
. Найдем координаты векторов 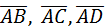 :
:
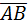 {1-1;0-2;-1(-3)}={0;-2;-2};
{1-1;0-2;-1(-3)}={0;-2;-2};
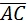 {2-1;4-2;-6-(-3)}={1;2;-3};
{2-1;4-2;-6-(-3)}={1;2;-3};
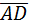 {0-1;-1-2;3-(-3)}={-1;-3;6}.
{0-1;-1-2;3-(-3)}={-1;-3;6}.
Найдем смешанное произведение 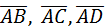 :
:
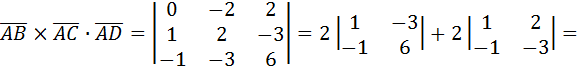
=2(6-3)=2(-3+2)=6-2=4.
Итак, VАВСD= 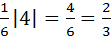 (куб.ед.).
(куб.ед.).
б) S∆АВС= 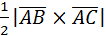 . Найдем векторное произведение векторов
. Найдем векторное произведение векторов 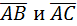 :
:
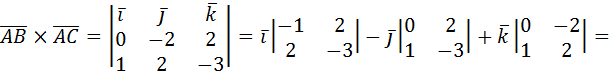
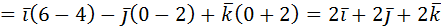 .
.
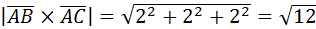 .
.
S∆АВС= 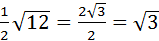 (кв.ед.)
(кв.ед.)
в) 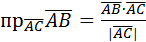 .
.
Найдем скалярное произведение векторов 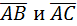 :
:
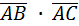 =0∙1+(-2)2+2(-2)=0-4-6=-10.
=0∙1+(-2)2+2(-2)=0-4-6=-10.
Найдем длину | 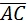 |=
|= 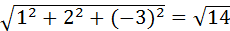 .
.
Итак, 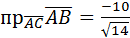 .
.
г) 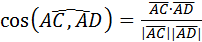 .Найдем скалярное произведение
.Найдем скалярное произведение 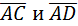 :
:
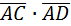 =1(-1)+2(-3)+(-3)6=-1-6-18=-25.
=1(-1)+2(-3)+(-3)6=-1-6-18=-25.
Найдем длину 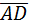 :
:
| 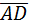 |=
|= 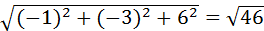 . Значит,
. Значит, 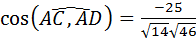 .
.
Ответ: а) 2/3 куб.ед.; б) 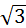 кв.ед. в)
кв.ед. в) 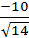 ; г)
; г) 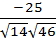 .
.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1.Найти длину вектора 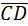 , если: С(1;-3;4), D(0;-2;1).
, если: С(1;-3;4), D(0;-2;1).
Ответ: | 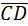 |=
|= 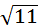 .
.
2. Найти длину радиус-вектора точки М(2;-3;6).
Ответ: 7.
3. Найти длину вектора 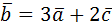 , если
, если 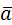 {2;-1;0},
{2;-1;0}, 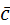 {3;-1;4}.
{3;-1;4}.
Ответ: 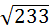 .
.
4.Найти направляющие косинусы вектора 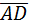 , если А(3;-5;4); D(2;-1;0).
, если А(3;-5;4); D(2;-1;0).
Ответ: cosα= 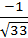 : cos
: cos 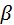 =
= 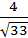 : cosγ=
: cosγ= 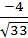 .
.
5. Даны векторы 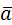 =2
=2 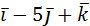 и
и 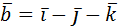 . Найти: а)
. Найти: а) 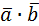 ; б)
; б) 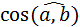 ; в)
; в) 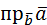 .
.
Ответ: а) 5; б) 5/9; в) 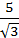 .
.
6. Даны векторы 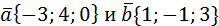 . Проверить, являются ли они ортогональными.
. Проверить, являются ли они ортогональными.
Ответ: не являются.
7. Вычислить работу силы 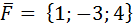 , если точка ее приложения перемещается прямолинейно из начала координат в положение М(1;-1;3).
, если точка ее приложения перемещается прямолинейно из начала координат в положение М(1;-1;3).
Ответ: 16.
8. Раскрыть скобки и упростить выражение:
1) 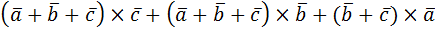 ;
;
2) 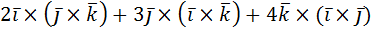 .
.
Ответ: 1) 2 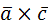 ; 2) 3.
; 2) 3.
9. Даны векторы 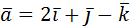 и
и 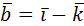 . Найти
. Найти 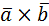 .
.
Ответ: 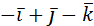 .
.
10. Найти площадь параллелограмма АВСD, если его вершины А(3;-2;4), В(0;-1;6), С(1;-3;6), D(1;-1;0).
Ответ: 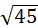 .
.
11. Сила 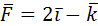 приложена в точке А(1;-1;0). Найти ее момент относительно точки В(2;-1;3).
приложена в точке А(1;-1;0). Найти ее момент относительно точки В(2;-1;3).
12. Проверить компланарность векторов 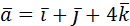 ,
,
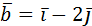 ,
, 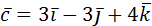 .
.
Ответ: компланарны.
13. Даны координаты вершин пирамиды А(4;4;10), В(7;10;2), С(2;8;4), D(9;6;9).
Найти: а) VАВСD; б) S∆АВС; в) 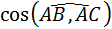 ; г)
; г) 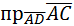 .
.
Ответ: а) 4; б) 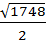 ; в)
; в) 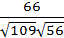 ; г)
; г) 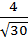 .
.
14. Найти угол между векторами 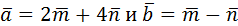 , где
, где 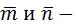 единичные векторы и угол между ними равен 120˚.
единичные векторы и угол между ними равен 120˚.
Ответ: -1/2.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Прямая линия на плоскости
Уравнением линии на плоскости ХОУ называется такое уравнение F(x,y)=0 с двумя переменными, которому удовлетворяют координаты х и у каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на линии.
Переменные х и у в уравнении линии называются текущими координатами точек линии.
Простейшей из линий является прямая.
Разным способам задания прямой соответствуют в прямоугольной системе координат различные виды ее уравнений (табл. 1).
Таблица 1
| № п/п | Вид уравнения | Смысл входящих в уравнение коэффициентов | Примечания |
| Уравнение с угловым коэффициентом y=kx+b | k – тангенс угла a наклона прямой к положительному направлению оси ОХ; b – отрезок, отсекаемый прямой от оси ОY | a≠π/2 | |
| Общее уравнение прямойАх+Ву+С=0 | А,В – координаты вектора, перпендикулярного прямой (нормального вектора) N | А,В не равны нулю одновременно | |
| Уравнение прямой, про-ходящей через данную точку в данном направ-ленииу-у0=k(х-х0 ) | т.М(х0,у0) – заданная точка; k – угловой коэффициент прямой | При различных k уравнение называется уравнением пучка прямых с центром в точке М(х0,у0) | |
Уравнение прямой, проходящей через две заданные точки 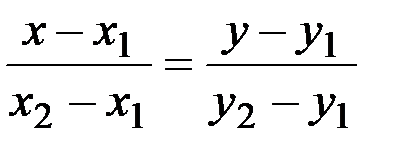 | т.М1(х1,у1), т.М2(х2,у2) – заданные точки | - | |
Уравнение прямой в отрезках на осях х 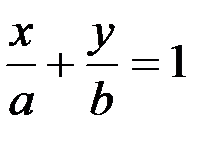 | а,b – отрезки, отсекаемые прямой от координатных осей ОХ и ОY соответственно | а≠0, b≠0 | |
| Уравнение прямой, проходящей через заданную точку параллельно заданному вектору | т.М0(х0,у0) – заданная точка; m,n – координаты вектора, параллельного искомой прямой ( направляющего век-тора)  | Такое уравнение часто называют каноническим | |
| № п/п | Вид уравнения | Смысл входящих в уравнение коэффициентов | Примечания |
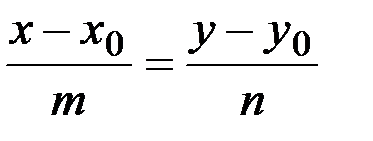 | |||
| Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору А(х-х0)+В(у-у0)=0 | т.М0(х0,у0) – заданная точка, А,В – координаты нормального вектора искомой прямой 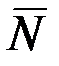 |
Угол между двумя прямыми
Пусть прямые l1и l2 заданы своими уравнениями с угловыми коэффициентами: l1: y=k1х+b1, l2:y=k2x+b2, тогда острый угол между двумя прямыми определяется его тангенсом по формуле
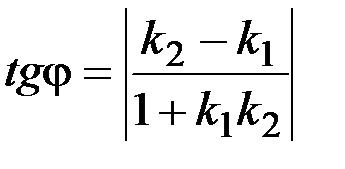 .
.
Если прямые l1и l2 заданы общими уравнениями А1х+В1у+С1=0 и А2х+В2у+С2=0, то угол между ними можно найти как угол между их нормальными векторами
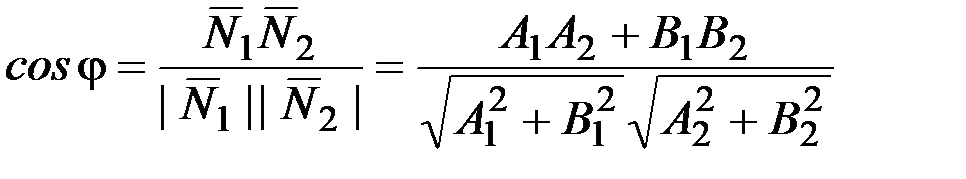 .
.
В случае задания прямых своими каноническими уравнениями
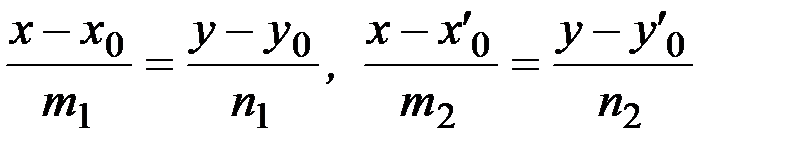 угол между прямыми находится как угол между направляющими векторами прямых
угол между прямыми находится как угол между направляющими векторами прямых
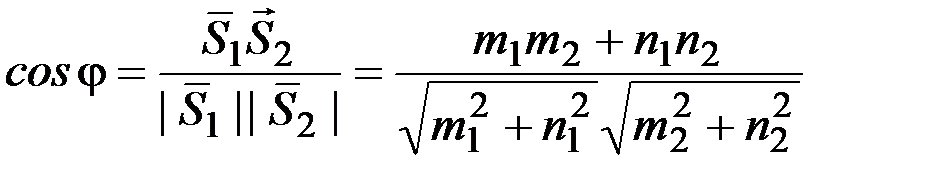 .
.
Условия параллельности и перпендикулярности прямых (табл. 2)
Таблица 2
| № п/п | Способ задания прямых | Условие параллельности прямых | Условие перпендикулярности прямых |
| l1: y=k1х+b, l2: y=k2x+b2 | k1=k2 | k1k2= -1 | |
| l1: А1х+В1у+С1=0 l2: А2х+В2у+С2=0 | 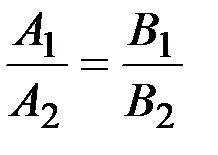 | A1A2+B1B2=0 | |
l1: 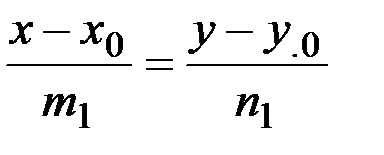 l2: l2: 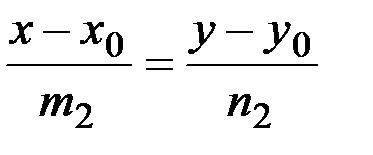 | 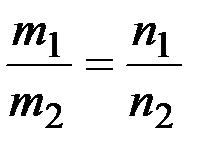 | m1m2+n1n2=0 |
Примеры решения типовых задач
1. Написать уравнение прямой, отсекающей на оси Оу отрезок b=-3 и составляющей с осью Ох угол 60˚.
Решение:
Воспользуемся уравнением прямой с угловым коэффициентом y=kx+b. По условию b=-3, а k=tgα=tg60˚=Ö3. Итак, у= 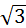 х-3 – уравнение искомой прямой.
х-3 – уравнение искомой прямой.
Ответ: у= 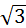 х-3.
х-3.
2. Определить параметры k и b для каждой из прямых:
1) 3х+4у=12;
2) 2х+3у=0;
3) у=-2;
4) 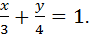
Решение:
1) 3х+4у=12; 2) 2х+3у=0; 3) y=-2; 4) 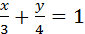 ;
;
4у=12-3х; 3y=-2x; k=0, b=-2. 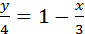 ;
;
у= 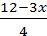 ; y=
; y= 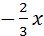 ; y=4-
; y=4- 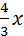 ;
;
y= 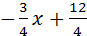 ; k=
; k= 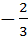 , b=0. y=-
, b=0. y=- 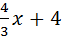 ;
;
y= 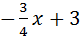 ; k=
; k= 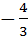 , b=4.
, b=4.
k= 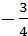 , b=3.
, b=3.
Ответ: 1) k= 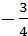 , b=3; 2) k=
, b=3; 2) k= 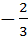 , b=0; 3) k=0, b=-2; 4) k=
, b=0; 3) k=0, b=-2; 4) k= 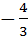 , b=4.
, b=4.
3. Дан треугольник с вершинами А(-1;1), В(1;5), С(3;-2). Написать уравнения сторон треугольника.
Решение:
Воспользуемся способом задания прямой по 2-м точкам:
АВ: 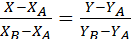 ; BC:
; BC: 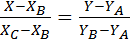 ; AC:
; AC: 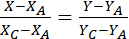 ;
;
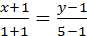 ;
; 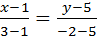 ;
; 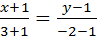 ;
;
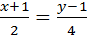 .
. 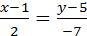 .
. 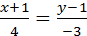 .
.
Ответ: АВ: 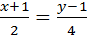 ; ВС:
; ВС: 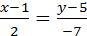 ; АС:
; АС: 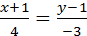 .
.
4. Дана прямая 2х+3у-3=0 и точка М0(1;-2). Написать уравнение прямой, проходящей через точку М0: а) параллельно заданной прямой; б) перпендикулярно заданной прямой.
Решение:
1-й способ.
а) Условие параллельности двух прямых k1=k2.
Пусть уравнение искомой прямой имеет вид y=k2x+b2; 3y=3-2x; y= 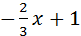 ; k1=
; k1= 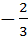 Þk2=
Þk2= 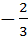 ; у=
; у= 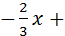 b2. Так как М0(1;-2) принадлежит прямой, то -2=
b2. Так как М0(1;-2) принадлежит прямой, то -2= 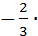 1+b2Þb2=-2+
1+b2Þb2=-2+  , b2=
, b2= 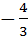 . Итак, y=
. Итак, y= 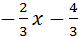 Û3у+2х+4=0.
Û3у+2х+4=0.
б) Условие перпендикулярности двух прямых k1k3=-1.
Пусть уравнение искомой прямой имеет вид y=k3x+b3;k1= 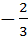 Þk3
Þk3 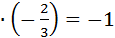 Þk3=
Þk3=  ; y=
; y=  x+b3. Так как М0(1;-2) принадлежит прямой, то -2=
x+b3. Так как М0(1;-2) принадлежит прямой, то -2= 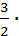 1+b3Þb3=-2
1+b3Þb3=-2 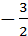 Þb3=
Þb3= 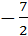 .
.
Итак, 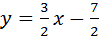 Þ3x-2у-7=0.
Þ3x-2у-7=0.
2-й способ.
l di54bWxMj8FOwzAQRO9I/IO1SFwq6pA0bQlxKlSJCxyAwgc4yZJE2OsQu6n79ywnuM1oRrNvy120 Rsw4+cGRgttlAgKpce1AnYKP98ebLQgfNLXaOEIFZ/Swqy4vSl207kRvOB9CJ3iEfKEV9CGMhZS+ 6dFqv3QjEmefbrI6sJ062U76xOPWyDRJ1tLqgfhCr0fc99h8HY5WwdPL6+KcxvXie5PX+zhvTXz2 Rqnrq/hwDyJgDH9l+MVndKiYqXZHar0w7LOU0QOL1R0ILmRpvgJRK9hkOciqlP8/qH4AAAD//wMA UEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5 cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAAvAQAAX3Jl bHMvLnJlbHNQSwECLQAUAAYACAAAACEAF3PNyvIBAADqAwAADgAAAAAAAAAAAAAAAAAuAgAAZHJz L2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAdpYf698AAAAJAQAADwAAAAAAAAAAAAAAAABMBAAA ZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAAFgFAAAAAA== " strokecolor="black [3040]"/>
 . . |
| М0(1;-2) |
| Рис.2 |
а) Из общего уравнения прямой 2х+3у-3=0 определяем координаты вектора нормали 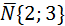 . Если искомая прямая параллельна заданной, то вектор
. Если искомая прямая параллельна заданной, то вектор 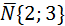 будет являться нормалью и к искомой прямой (рис.2). Мы имеем нормаль и точку М0(1;-2), через которую проходит искомая прямая, поэтому используем уравнение прямой, проходящей через точку М(х0,у0) перпендикулярно вектору
будет являться нормалью и к искомой прямой (рис.2). Мы имеем нормаль и точку М0(1;-2), через которую проходит искомая прямая, поэтому используем уравнение прямой, проходящей через точку М(х0,у0) перпендикулярно вектору 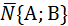 . А(х-х0)+В(у-у0)=0, 2(х-1)+3(у+2)=0, 2х+3у+4=0.
. А(х-х0)+В(у-у0)=0, 2(х-1)+3(у+2)=0, 2х+3у+4=0.
б) Если искомая прямая l1 (рис.3) перпендикулярна заданной l, то вектор 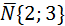 будет параллелен прямой l1, и мы возьмем его в качестве направляющего вектора искомой прямой
будет параллелен прямой l1, и мы возьмем его в качестве направляющего вектора искомой прямой 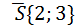 .
.
| l |
| l1 |
| 2х+3у-3=0 |
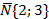 . . |
| М(1;-2) |
| Рис.3 |
Используем уравнение прямой, проходящей через точку М(х0,у0) параллельно вектору 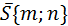 .
. 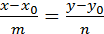 . У нас
. У нас 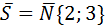 .
. 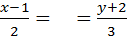 ; 3х-3=2у+4, 3х-2у-7=0.
; 3х-3=2у+4, 3х-2у-7=0.
Ответ: 2х+3у+4=0, 3х-2у-7=0.
2. Найти расстояние от точки М0(2;-1) до прямой 3х+4у-22=0.
Решение:
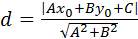 ; х0=2; у0=-1.
; х0=2; у0=-1.
А=3; В=4; С=-22.
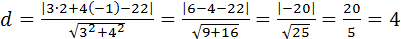 .
.
Ответ: 4.
Плоскость в пространстве
Любое уравнение первой степени в трехмерном пространстве определяет какую-либо плоскость.
Разным способам задания плоскости соответствуют различные виды уравнений (табл. 3.)
Таблица 3
| № п/п | Вид уравнения | Смысл входящих в уравнение коэффициентов | Примечание |
| Уравнение плоскости, проходящей через данную точку перпендикулярно заданному вектору А(х-х0)+В(у-у0)+С(z-z0)=0 | (x0,y0,z0) – координаты заданной точки; АВС – координаты заданного вектора | Вектор N(А,В,С) называется нормальным вектором плоскости | |
| Общее уравнение плоскости Ах+Ву+Сz+D=0 | D=-Ax0-By0-Cz0, АВС – нормальный вектор плоскости; | Это уравнение получается из уравнения (1) эле-ментарными | |
| № п/п | Вид уравнения | Смысл входящих в уравнение коэффициентов | Примечание |
| х0,y0,z0 – координаты данной точки | преобразованиями | ||
Уравнение плоскости, проходящей через три заданные точки 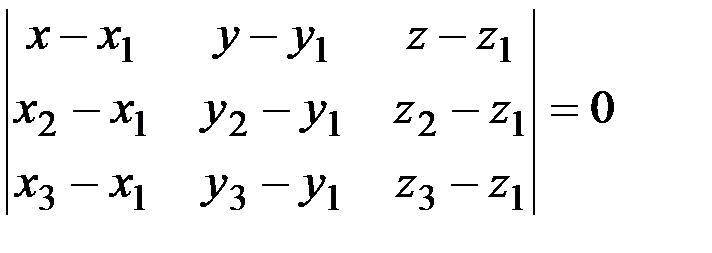 | М1(х1,y1,z1), М2(х2,y2,z2), М3(х3,y3,z3) – три точки, заданные своими координатами | Точки М1, М2, М3 не должны лежать на одной прямой | |
Уравнение плоскости в отрезках на осях 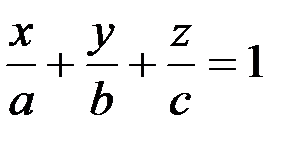 | а,b,c – отрезки, отсекаемые плоскостью от осей координат | аbc≠0 |
Пусть даны две плоскости a1 и a2:
a1: А1х +В1у+С1z+D1=0,
a2: А2х +В2у+С2z+D2=0.
Угол между двумя плоскостями определяется как 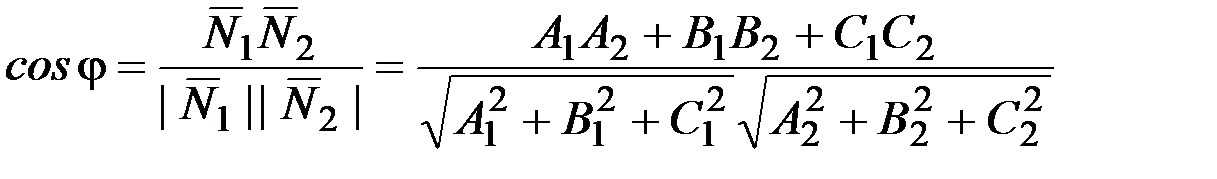 .
.
Условие перпендикулярности двух плоскостей:
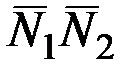 =0, то есть
=0, то есть 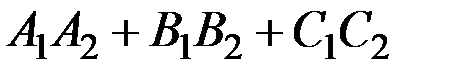 =0.
=0.
Условие параллельности двух плоскостей:
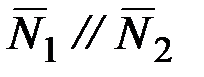 или
или 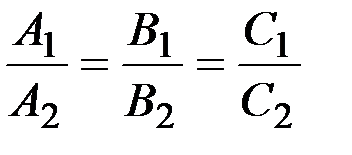 .
.
Расстояние от точки до плоскости:
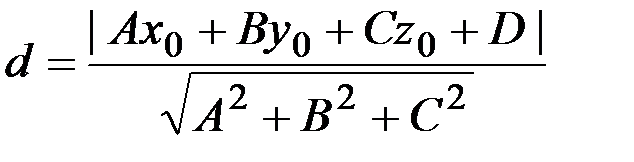 ,
,
где Ах+Ву+Сz+D=0 – заданная плоскость; М(x0,y0,z0) – данная точка.
Примеры решения типовых задач
1. Написать уравнение плоскости, проходящей через точку М(-1;1,3) перпендикулярно вектору 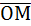 .
.
Решение:
Найдем координаты вектора 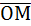 : О(0;0;0); М(-1;1;3) Þ
: О(0;0;0); М(-1;1;3) Þ
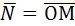 {-1;1;3}.
{-1;1;3}.
Уравнение плоскости имеет вид:
A(x-x0)+B(y-y0)+C(z-z0)=0
А=-1, В=1, С=3 – координаты вектора нормали.
X0=-1, y0=1, z0=3.
-1(х+1)+1(у-1)+3(z-3)=0
-х-1+у-1+3z-9=0
-х+у+3z-11=0.
Ответ: -х+у+3z-11=0.
2.Написать уравнение плоскости, проходящей через точки М1(1;-1;3), М2(2;-1;0), М3(4;2;-1).
Решение:
Уравнение плоскости, проходящей через три точки имеет вид:
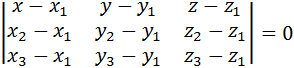 ,
,
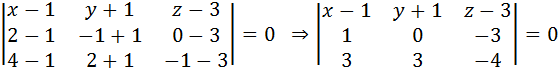
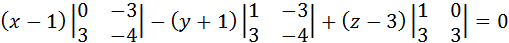 ,
,
9(х-1)-5(у+1)+3(z-3)=0
9х-9-5у-5+3z-9=0
9х-5у+3z-23=0.
Ответ: 9х-5у+3z-23=0.
3. Написать уравнение плоскости, проходящей через точку М0(-2;7;3) параллельно плоскости х-4у+5z+1=0 (рис.10).
 {1;-4;5} {1;-4;5} |
| М0(-2;7;3) |
| Рис. 10 |
Решение:
Нормальный вектор для плоскости х-4у+5z+1=0 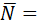 {1;-4;5} является нормальным для искомой плоскости. Так как плоскость проходит через точку М0(-2;7;3), то уравнение плоскости имеет вид:
{1;-4;5} является нормальным для искомой плоскости. Так как плоскость проходит через точку М0(-2;7;3), то уравнение плоскости имеет вид:
A(x-x0)+B(y-y0)+C(z-z0)=0;
1(х+2)-4(у-7)+5(z-3)=0;
х+2-4у+28+5z-15=0;
х-4у+5z+15=0.
Ответ: х-4у+5z+15=0.
4. Найти расстояние от точки М0(1;-1;3) до плоскости 13х+2у- -5z+1=0.
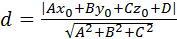 ; х0=1; у0=-1; z0=3.
; х0=1; у0=-1; z0=3.
А=13; В=2; С=-5, D=1.
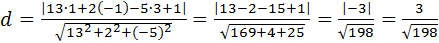 .
.
Ответ: d= 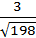 .
.
5. Найти угол между плоскостями х+у-1=0 и 2х-у+3z-1=0.
Решение:
Угол между плоскостями определяем как угол между нормалями к этим плоскостям. Из общих уравнений плоскостей определяем координаты нормалей 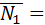 {1;1;0},
{1;1;0}, 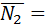 {2;-1;3}.
{2;-1;3}.
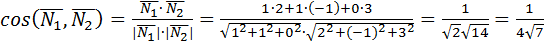 .
.
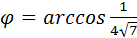 .
.
Ответ: 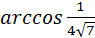 .
.
Прямая в пространстве.
Прямая и плос<
