Вопрос 8. Характеристическое уравнение ЭЦ и метод его получения

Характеристическое уравнение позволяет получить качественное представление о переходном процессе в ЭЦ. Количество уравнений в общем случае равно его порядку, а порядок уравнения определяется количеством независимых реактивных элементов ЭЦ.

Свойства корней ХУ:

1)уравнение первой степени имеет всегда отрицательный действительный корень

2)уравнение второй степени может иметь:

ð два действительных неравных корня < 0

ð 2 действительных равных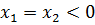

ð 2 комплексно – сопряженных корня с действительной частью < 0

3)уравнение третьей степени может иметь:

ð 3 действительных корня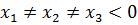

ð 3 действительных отрицательных корня, из которых 2 равны друг другу

ð три действительных равных корня меньше 0

4) 1 действительный отрицательный и 2 комплексно – сопряженных с отрицательной действительной частью

Метод входного сопротивления (входной проводимости)

· Составляем цепь, соответствующую свободному режиму (для этого удаляем все источники электрической энергии: источники ЭДС замыкаем накоротко, ветви с источниками тока размыкаем).

· Размыкаем цепь в произвольном месте и относительно точек разрыва записываем входное комплексное сопротивление 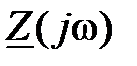, при этом комплекс емкостного сопротивления 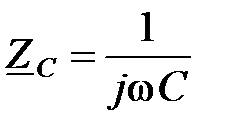, а индуктивного .

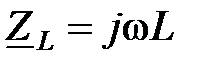· В полученном выражении повсеместно величину 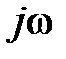заменяем корнем p и приравниваем выражение к нулю.

· Уравнение 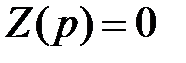является характеристическим уравнением.

Следует отметить, что для цепей, содержащих большое количество параллельных ветвей, удобно пользоваться методом входной проводимости. Метод состоит в том, что записывается эквивалентная комплексная проводимость между двумя произвольными узлами послекоммутационной цепи с отключёнными источниками. Далее, как и в предыдущем случае, jw заменяется на р и решается уравнение .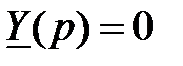

Метод главного определителя

· Составляем цепь, соответствующую свободному режиму.

· Выбираем независимые контуры и задаем направление их контурных токов.

· Составляем главный определитель 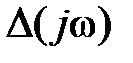, состоящий из собственных и общих контурных комплексных сопротивлений.

· Повсеместно заменяем 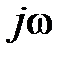на p и приравниваем нулю.

· Уравнение 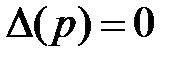– характеристическое уравнение

.

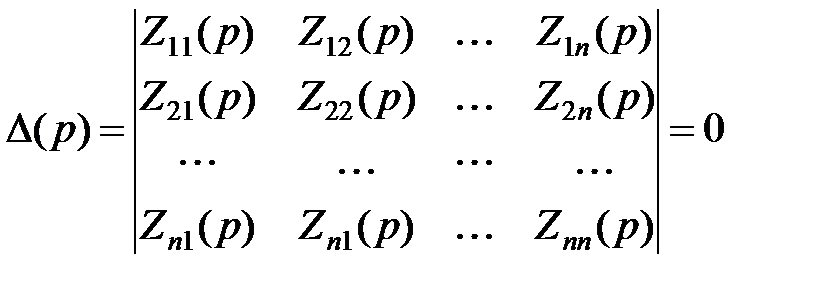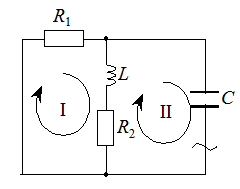Метод главного определителя. Выберем независимые контуры и укажем направление их обхода . Составим главный определитель, заменяя 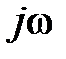на p

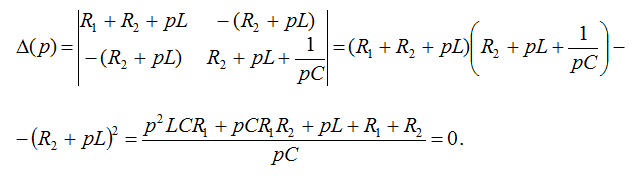
Существует еще один способ, основанный на определении постоянной времени, применимый только для цепей I порядка.

Постоянной времени t цепи называют промежуток времени, за который искомая величина изменится в е раз. Время переходного процесса прямо пропорционально t и приближённо равно: .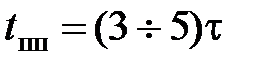

Для устойчивых цепей (цепей, в которых соблюдается условие 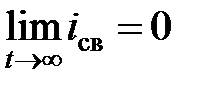) корни характеристического уравнения должны быть отрицательными или иметь отрицательную действительную часть. Постоянная времени для цепей I порядка связана с корнем характеристического уравнения: .

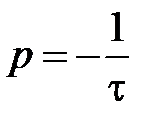Причём для цепей, содержащих ёмкость, – t = R_эС, а для цепей, содержащих индуктивность, – t=L/R_э, где R_э – эквивалентное сопротивление послекоммутационной цепи, вычисленное относительно зажимов единственного реактивного элемента (накопителя энергии) при удаленных источниках.