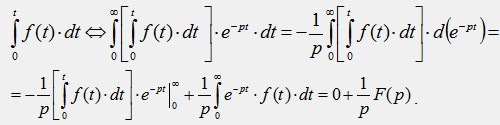Вопрос 6. В чем состоит преимущество операторного метода анализа электрических цепей перед классическим?
Классический метод расчета обладает несомненными достоинствами, обусловленными физической наглядностью связей между величинами, которые выражаются дифференциальными уравнениями Кирхгофа, и сравнительной простотой их совместного решения. Часто, однако, задачи при решении классическим методом приводят к громоздким выкладкам, связанным, главным образом, с отысканием постоянных интегрирования, причем, эта процедура усложняется с ростом порядка цепи.
Отмеченные недостатки отсутствуют при применении операторного метода, в соответствии с которым уравнения переходного процесса в линейных цепях, представляющие собой линейные дифференциальные уравнения с постоянными коэффициентами, можно интегрировать операторным методом, основанном на преобразовании Лапласа.
При расчете операторным методом не нужно определять постоянные интегрирования из начальных условии решением какой-либо системы уравнений. Кроме того, при расчете изображений в эквивалентных операторных схемах можно пользоваться всеми ранее известными методами расчета цепей при установившихся режимах
Вопрос 7. Прямое и обратное преобразование Лапласа и их применение для анализа электрических цепей
Преобразованием Лапласа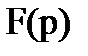 
функции 
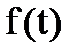является функция комплексной переменной вида: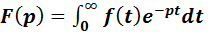 
Существует обратное преобразование Лапласа:
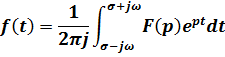
Перечислим основные свойства преобразования Лапласа:
Линейность (сумма всех оригиналов есть сумма всех изображений)
Если оригинал представлен суммой функций, то изображение этой суммы равно сумме изображений этих функций (изображение линейной комбинации функций есть линейная комбинация изображений)
Если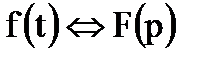 
, то 
.
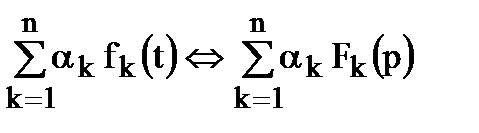Дифференцирование оригинала
Если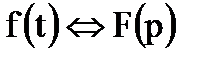 
, то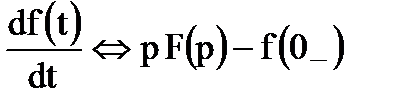 
.
3. Интегрирование оригиналасводится к делению изображения на р
Если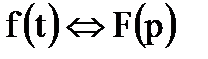 
, то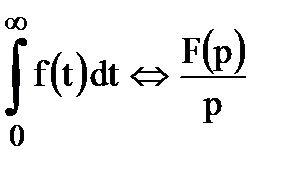 
.
4. Сжатие (теорема подобия - Теорема позволяет определить изображение функции времени при изменении масштаба её аргумента.)
Если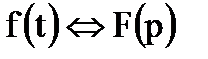 
, то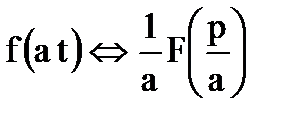 
.
5. Запаздывание (Теорема позволяет определить изображение функции f(t – t0) , отличающейся от функции f(t) тем, что она сдвинута вправо вдоль оси времени на t0)
Если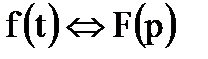 
, то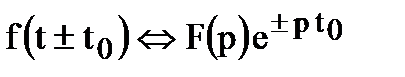 
.
6. Смещение (Теорема смещения позволяет определить, как изменяется изображение при умножении оригинала на показательную функцию e ±at, где a - постоянное число)
Если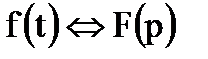 
, то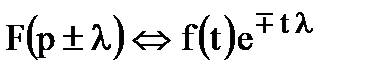 
.
Свертка
Если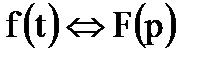 
, то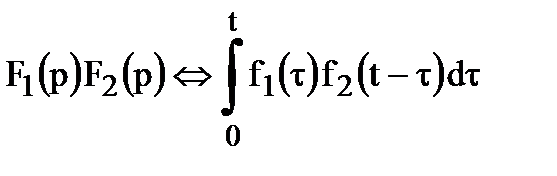 
.
8. Предельные соотношения:
.
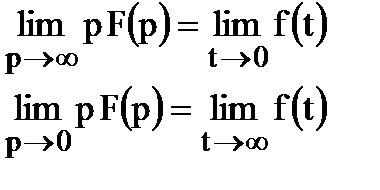Операторные изображения некоторых функций:
| Оригинал (f(t)) | Изображение (F(p)) |
| A |  |
 |  |
 |  |
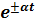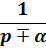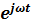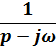| sinwt |  |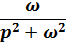
| coswt |  |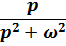
| sin(wt+y) |  |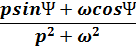
1) Изображение постоянной функции f(t)=А:
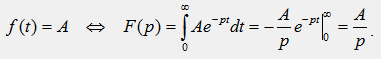
2) Изображения экспоненциальных функций:
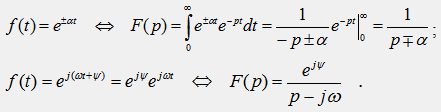
3) Изображения гармонических функций:
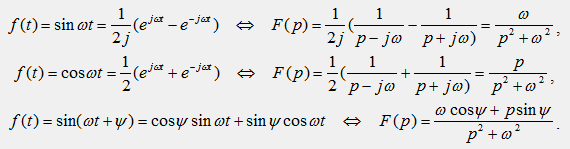
5) Изображения 1-ой и 2-ой производной от функции времени:
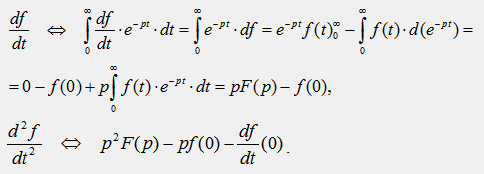
6) Изображение определенного интеграла от функции:
