Вопрос 1. Что понимается под переходным процессом в электрической цепи? Какова его длительность? Чем обусловлены переходные процессы в электрических цепях? Существуют ли цепи, в которых их нет?

Длинные линии

1. Дать определение длинной линии и перечислить ее свойства и параметры.

2. Какие условия работы длинной линии Вы знаете? Какие особенности поведения линии имеют место в разных условиях?

3. Что понимается под первичными и вторичными параметрами длинной линии и какова связь между ними?

4. Что такое коэффициент распространения и волновое сопротивление длинной линии. Как их использовать?

5. Как определяются коэффициенты отражения тока и напряжения в длинной линии?

6. Представить эквивалентную схему замещения элементарного отрезка длинной линии и уравнения, отражающие его поведение.

Вопрос 1. Что понимается под переходным процессом в электрической цепи? Какова его длительность? Чем обусловлены переходные процессы в электрических цепях? Существуют ли цепи, в которых их нет?

Установившийся режим – состояние цепи, в котором все токи и напряжения являются периодическими функциями времени, либо постоянными величинами (в цепях постоянного тока).

Переходный процесс – переход из одного установившегося состояния в другое. Такой процесс возникает, например, при резком изменении сопротивления цепи. Если в ЭЦ имеется только источники ЭДС или тока и активные сопротивления, то переход от одного установившегося режима к другому происходит мгновенно, то есть без ПП.

Возникновение ПП объясняется тем, что в индуктивностях и емкостях цепи энергия не может измениться мгновенно, так как для осуществления этого необходимы источники, имеющие бесконечно большую мощность. ПП не протекает в цепях, где отсутствуют реактивные элементы.

На практике длительность ПП равна 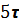,в теории длительность ПП равна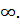

Вопрос 2. Что понимается под коммутацией? Как долго она длится? Сформулируйте законы коммутации. Каковы схемы замещения катушки индуктивности и конденсатора в момент коммутации и установившемся режиме?

Коммутация –любое скачкообразное изменение в цепи, приводящее к нарушению установившегося режима. Принято считать, что коммутация происходит мгновенно в момент времени t=0, с помощью идеального ключа или ступенчатого сигнала.

Коммутирующее устройство на схеме изображают в виде идеального ключа, у которого при замыкании сопротивление равно нулю, а в разомкнутом состоянии равно бесконечности:

K

При анализе ПП в цепи, как правило, можно пренебречь длительностью процесса коммутации, то есть считать, что коммутация осуществляется практически мгновенно. Начало отсчета времени ПП обычно совмещают с моментом коммутации, причем через 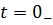обозначают, момент времени, непосредственно предшествующий коммутации.

Законы коммутации используются для определения начальных условий при расчете переходных процессов.

I ЗК: в начальный момент времени после коммутации ток индуктивности сохраняет такое же значение как и непосредственно перед коммутацией: 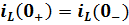, а затем плавно изменяется, начиная с этого значения;

II ЗК: в начальный момент времени после коммутации напряжение на емкости сохраняет такое же значение, как и непосредственно перед коммутацией: 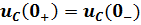, а затем плавно изменяется, начиная с этого значения.

Начальные значения величин, сохраняющиеся неизменными в момент времени t = 0, называются независимыми начальными условиями. Таковыми являются токи индуктивностей и напряжения на ёмкостях, подчиняющиеся правилам коммутации. Токи и напряжения сопротивлений, токи ёмкостей и напряжения на индуктивностях в момент коммутации могут изменяться скачком. Их величины после коммутации (t = 0⁺) называют зависимыми начальными значениями. Последние не определяются непосредственно правилами сохранения, но всегда могут быть выражены через независимые начальные значения с помощью уравнений Кирхгофа, записанных для мгновенных значений токов и напряжений, действующих в послекоммутационной цепи для момента t = 0⁺.

Если в момент коммутации токи всех индуктивных и напряжения всех емкостных элементов равны нулю, то НУ называются нулевыми.

В момент коммутации (t = 0) в общем случае индуктивность можно заменить источником тока с 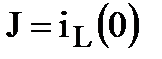, а емкость – источником напряжения с 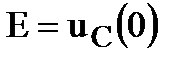. В частном случае при 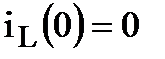и и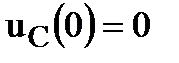ндуктивность заменяется обрывом, а емкость – коротким замыканием.

Конечные условия – это значение токов и напряжений в установившемся режиме при t = ∞.

Схемы замещения реактивных элементов для установившегося режима постоянного тока:

Законы коммутации могут не выполняться и при некоторых коммутациях, затрагивающих ветви, содержащие реактивные элементы. Коммутации такого типа называются некорректными. Анализ процессов в цепях при некорректных коммутациях производят с использованием принципов непрерывности потокосцепления 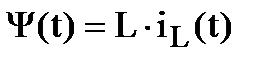и электрического заряда :

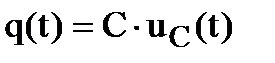Принцип непрерывности потокосцепления– алгебраическая сумма потокосцеплений индуктивностей в любом замкнутом контуре электрической цепи являются непрерывными функциями времени:

.

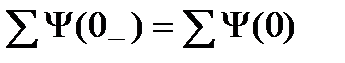Принцип непрерывности электрического заряда – алгебраическая сумма зарядов ёмкостей, подключённых к любому узлу электрической цепи, являются непрерывными функциями времени:

.

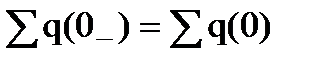Некорректность коммутации возникает вследствие излишне упрощенного рассмотрения процесса коммутации и может быть устранена при более строгом анализе.

Этап 1.

	Ток в индуктивности до коммутации: 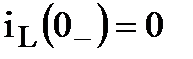, поскольку ключ разомкнут.
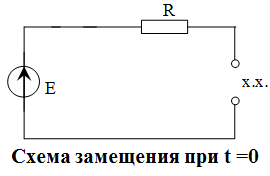	Согласно I закону коммутации: 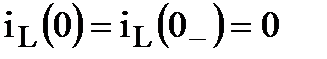–индуктивность заменяем разрывом.

Этап 2.

На основании законов Кирхгофа составим дифференциальное уравнение (этап № 2) относительно переменной тока в индуктивности по схеме после коммутации, описывающей мгновенные значения токов и напряжений.

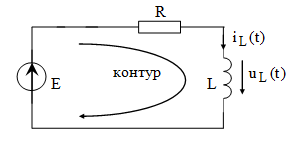Согласно II з-ну Кирхгофа:

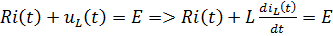– НДУ

Решение в виде:

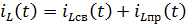
1) Определим свободную составляющую, решая ОДУ

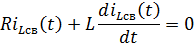
Из ОДУ получим характеристическое уравнение (этап № 3), осуществляя замену 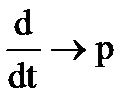. 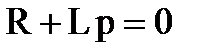, откуда 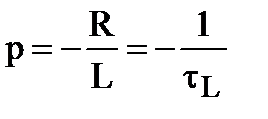[c^-1],

где 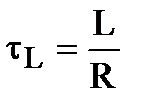[c] – постоянная RL-цепи.

Знак «минус» в выражении 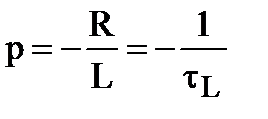указывает на то, что переходный процесс заканчивается и наступает установившийся режим.

Поскольку корень характеристического уравнения отрицательный и вещественный, то 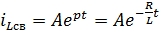– свободная составляющая (этап № 4) переходного тока.

2) Определим принуждённую составляющую (1 способ). Поскольку внешнее воздействие является постоянным, т.е. 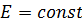, то решение для принуждённой составляющей будем искать в виде: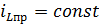

Осуществляя подстановку последнего соотношения в НДУ, получим: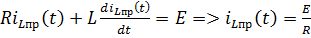

Определим принужденную составляющую тока в индуктивности

при t = ∞ (2 способ).

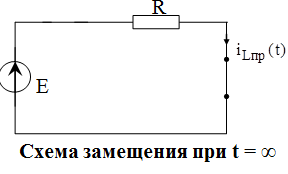
Индуктивность заменяем перемычкой.

На основании закона Ома: 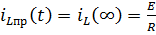– конечное условие.

3) Таким образом, вид переходного тока в индуктивности определяется в виде: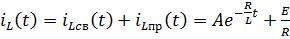

4) Определим const A (этап № 6), используя начальное условие .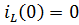

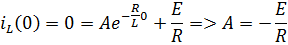
ð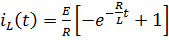

5) Переходные напряжения на индуктивности и резисторе:

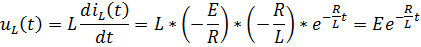
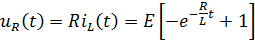
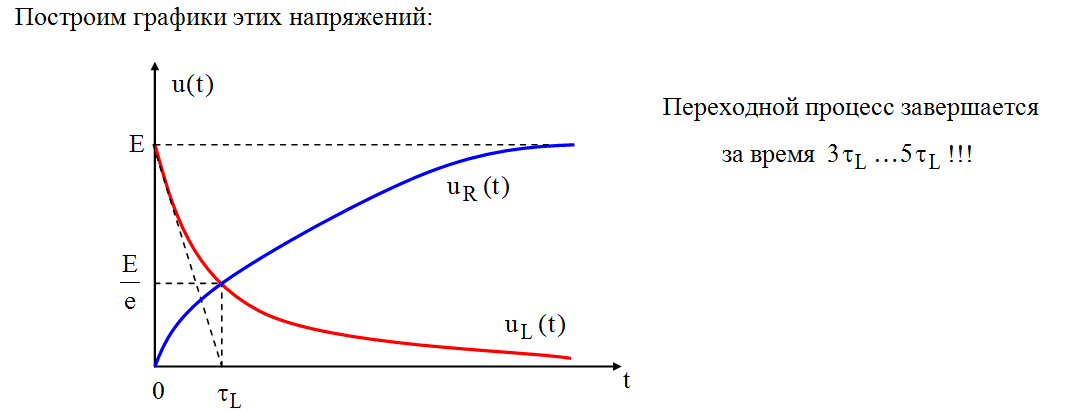
Постоянная времени последовательной RL-цепи 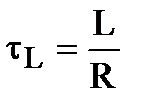графически определяется длиной подкасательной кривой 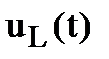при любом значении .

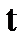Дифференцирование оригинала

Если 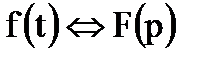, то .

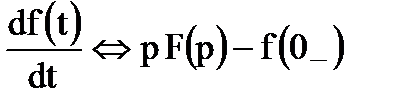3. Интегрирование оригиналасводится к делению изображения на р

Если 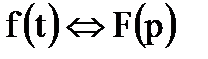, то .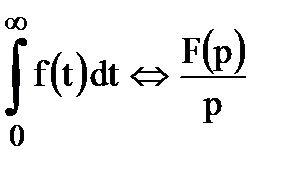

Сжатие (теорема подобия)

Если 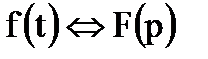, то .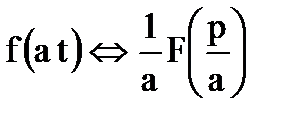

Запаздывание

Если 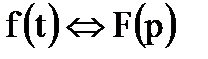, то .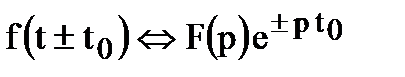

Смещение

Если 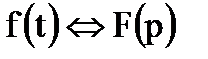, то .

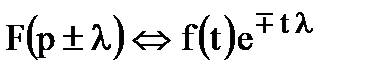Свертка

Если 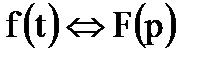, то .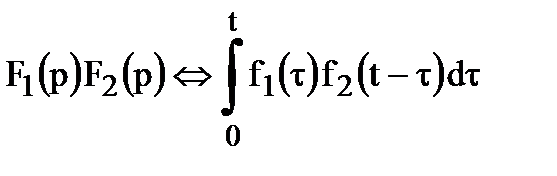

8. Предельные соотношения:

.

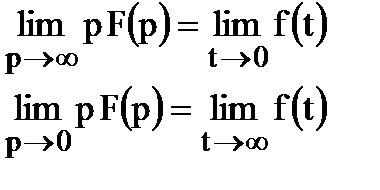Оригинал функции можно найти и с помощью теоремы разложения.

Если изображение функции представлено в виде дроби

,

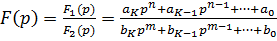причем многочлены (относительно р) F1(p) и F2(p) удовлетворяют следующим условиям:

- степень 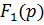ниже степени ,

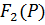- а_к и b_k – вещественные числа,

тооригинал находим по формул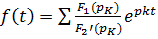е , где 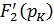– значение производной при р = р_к, 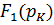– значение числителя при р = р_к.

В том случае, если один из корней равен нулю, то

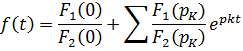
Дифференцирование оригинала

Если 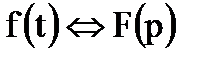, то .

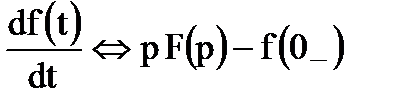3. Интегрирование оригиналасводится к делению изображения на р

Если 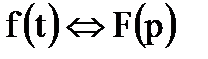, то .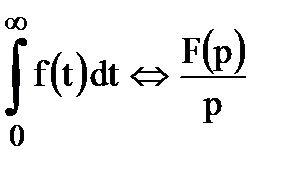

4. Сжатие (теорема подобия - Теорема позволяет определить изображение функции времени при изменении масштаба её аргумента.)

Если 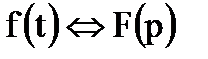, то .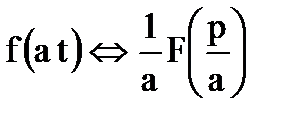

5. Запаздывание (Теорема позволяет определить изображение функции f(t – t0) , отличающейся от функции f(t) тем, что она сдвинута вправо вдоль оси времени на t0)

Если 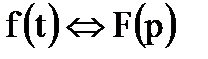, то .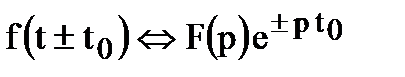

6. Смещение (Теорема смещения позволяет определить, как изменяется изображение при умножении оригинала на показательную функцию e ^±at, где a - постоянное число)

Если 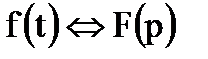, то .

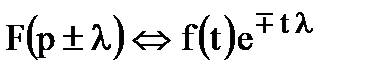Свертка

Если 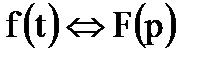, то .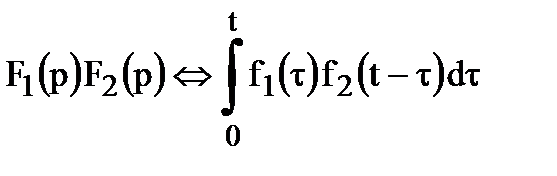

8. Предельные соотношения:

.

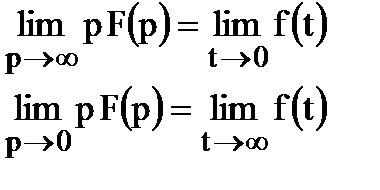Операторные изображения некоторых функций:

Оригинал (f(t))	Изображение (F(p))
A
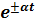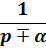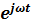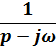sinwt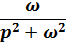
coswt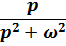
sin(wt+y)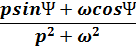

1) Изображение постоянной функции f(t)=А:

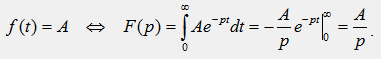
2) Изображения экспоненциальных функций:

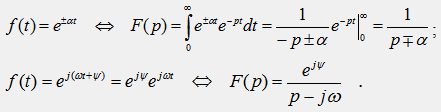
3) Изображения гармонических функций:

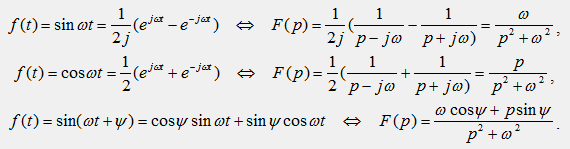
5) Изображения 1-ой и 2-ой производной от функции времени:

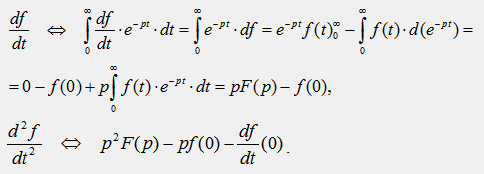
6) Изображение определенного интеграла от функции:

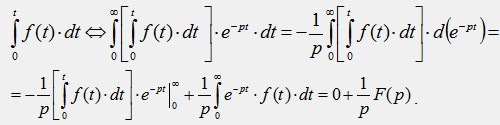
Метод главного определителя

· Составляем цепь, соответствующую свободному режиму.

· Выбираем независимые контуры и задаем направление их контурных токов.

· Составляем главный определитель 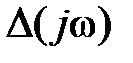, состоящий из собственных и общих контурных комплексных сопротивлений.

· Повсеместно заменяем 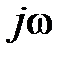на p и приравниваем нулю.

· Уравнение 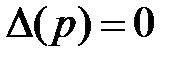– характеристическое уравнение

.

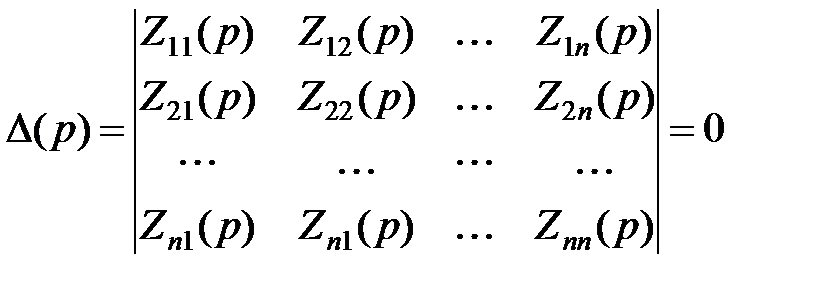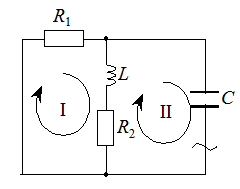Метод главного определителя. Выберем независимые контуры и укажем направление их обхода . Составим главный определитель, заменяя 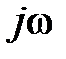на p

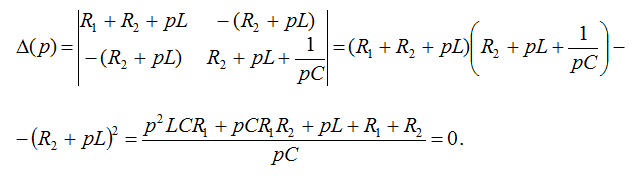
Существует еще один способ, основанный на определении постоянной времени, применимый только для цепей I порядка.

Постоянной времени t цепи называют промежуток времени, за который искомая величина изменится в е раз. Время переходного процесса прямо пропорционально t и приближённо равно: .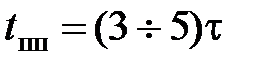

Для устойчивых цепей (цепей, в которых соблюдается условие 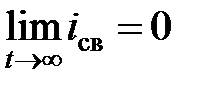) корни характеристического уравнения должны быть отрицательными или иметь отрицательную действительную часть. Постоянная времени для цепей I порядка связана с корнем характеристического уравнения: .

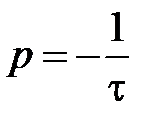Причём для цепей, содержащих ёмкость, – t = R_эС, а для цепей, содержащих индуктивность, – t=L/R_э, где R_э – эквивалентное сопротивление послекоммутационной цепи, вычисленное относительно зажимов единственного реактивного элемента (накопителя энергии) при удаленных источниках.

Длинные линии

1. Дать определение длинной линии и перечислить ее свойства и параметры.

2. Какие условия работы длинной линии Вы знаете? Какие особенности поведения линии имеют место в разных условиях?

3. Что понимается под первичными и вторичными параметрами длинной линии и какова связь между ними?

4. Что такое коэффициент распространения и волновое сопротивление длинной линии. Как их использовать?

5. Как определяются коэффициенты отражения тока и напряжения в длинной линии?

6. Представить эквивалентную схему замещения элементарного отрезка длинной линии и уравнения, отражающие его поведение.

Вопрос 1. Что понимается под переходным процессом в электрической цепи? Какова его длительность? Чем обусловлены переходные процессы в электрических цепях? Существуют ли цепи, в которых их нет?

Установившийся режим – состояние цепи, в котором все токи и напряжения являются периодическими функциями времени, либо постоянными величинами (в цепях постоянного тока).

Переходный процесс – переход из одного установившегося состояния в другое. Такой процесс возникает, например, при резком изменении сопротивления цепи. Если в ЭЦ имеется только источники ЭДС или тока и активные сопротивления, то переход от одного установившегося режима к другому происходит мгновенно, то есть без ПП.

Возникновение ПП объясняется тем, что в индуктивностях и емкостях цепи энергия не может измениться мгновенно, так как для осуществления этого необходимы источники, имеющие бесконечно большую мощность. ПП не протекает в цепях, где отсутствуют реактивные элементы.

На практике длительность ПП равна 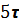,в теории длительность ПП равна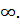

Вопрос 2. Что понимается под коммутацией? Как долго она длится? Сформулируйте законы коммутации. Каковы схемы замещения катушки индуктивности и конденсатора в момент коммутации и установившемся режиме?

Коммутация –любое скачкообразное изменение в цепи, приводящее к нарушению установившегося режима. Принято считать, что коммутация происходит мгновенно в момент времени t=0, с помощью идеального ключа или ступенчатого сигнала.

Коммутирующее устройство на схеме изображают в виде идеального ключа, у которого при замыкании сопротивление равно нулю, а в разомкнутом состоянии равно бесконечности:

K

При анализе ПП в цепи, как правило, можно пренебречь длительностью процесса коммутации, то есть считать, что коммутация осуществляется практически мгновенно. Начало отсчета времени ПП обычно совмещают с моментом коммутации, причем через 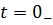обозначают, момент времени, непосредственно предшествующий коммутации.

Законы коммутации используются для определения начальных условий при расчете переходных процессов.

I ЗК: в начальный момент времени после коммутации ток индуктивности сохраняет такое же значение как и непосредственно перед коммутацией: 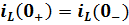, а затем плавно изменяется, начиная с этого значения;

II ЗК: в начальный момент времени после коммутации напряжение на емкости сохраняет такое же значение, как и непосредственно перед коммутацией: 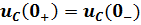, а затем плавно изменяется, начиная с этого значения.

Начальные значения величин, сохраняющиеся неизменными в момент времени t = 0, называются независимыми начальными условиями. Таковыми являются токи индуктивностей и напряжения на ёмкостях, подчиняющиеся правилам коммутации. Токи и напряжения сопротивлений, токи ёмкостей и напряжения на индуктивностях в момент коммутации могут изменяться скачком. Их величины после коммутации (t = 0⁺) называют зависимыми начальными значениями. Последние не определяются непосредственно правилами сохранения, но всегда могут быть выражены через независимые начальные значения с помощью уравнений Кирхгофа, записанных для мгновенных значений токов и напряжений, действующих в послекоммутационной цепи для момента t = 0⁺.

Если в момент коммутации токи всех индуктивных и напряжения всех емкостных элементов равны нулю, то НУ называются нулевыми.

В момент коммутации (t = 0) в общем случае индуктивность можно заменить источником тока с 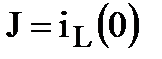, а емкость – источником напряжения с 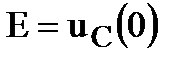. В частном случае пр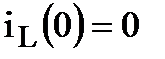и и 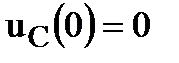индуктивность заменяется обрывом, а емкость – коротким замыканием.

Конечные условия – это значение токов и напряжений в установившемся режиме при t = ∞.

Схемы замещения реактивных элементов для установившегося режима постоянного тока:

Законы коммутации могут не выполняться и при некоторых коммутациях, затрагивающих ветви, содержащие реактивные элементы. Коммутации такого типа называются некорректными. Анализ процессов в цепях при некорректных коммутациях производят с использованием принципов непрерывности потокосцепления 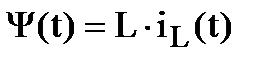и электрического заряда :

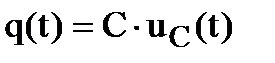Принцип непрерывности потокосцепления– алгебраическая сумма потокосцеплений индуктивностей в любом замкнутом контуре электрической цепи являются непрерывными функциями времени:

.

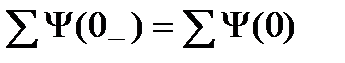Принцип непрерывности электрического заряда – алгебраическая сумма зарядов ёмкостей, подключённых к любому узлу электрической цепи, являются непрерывными функциями времени:

.

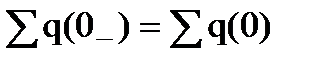Некорректность коммутации возникает вследствие излишне упрощенного рассмотрения процесса коммутации и может быть устранена при более строгом анализе.