Определители квадратных матриц и их свойства
Вопросы
1. Определитель второго порядка.
2. Формула для нахождения определителя третьего порядка.
3. Схема нахождения определителя третьего порядка по правилу треугольников.
4. Что такое минор элемента определителя.
5. Как найти алгебраическое дополнение элемента определителя.
6. Теорема разложения для определителя третьего порядка.
7. В каких случаях определитель заведомо равен нулю.
8. Что происходит с определителем, если поменять местами два его столбца.
9. Что происходит с определителем, если поменять местами две его строки.
10. Что происходит с определителем, если матрицу транспонировать.
11. В чем заключается элементарное преобразование определителей.
12. Как найти определитель любого произвольного порядка.
Задачи
29. Вычислить определители второго порядка:
а) 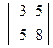 ; б)
; б) 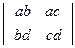 ;
;
в) 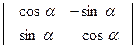 ; г)
; г) 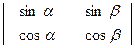 .
.
30. Вычислить определители третьего порядка:
а) 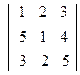 ; б)
; б) 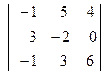 ;
;
в) 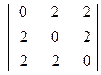 ; г)
; г) 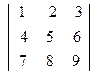 ;
;
д) 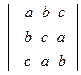 ; е)
; е) 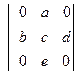 .
.
31. Вычислите определитель, используя теорему разложения:
а) 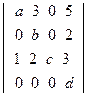 ; б)
; б) 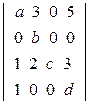 ; в)
; в) 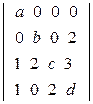 ;
;
г) 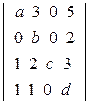 ; д)
; д) 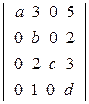 ; е)
; е) 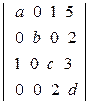 .
.
32. Вычислите определитель, разложив по третьей строке: 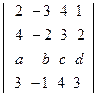 .
.
33. Вычислите определитель, разложив по второму столбцу: 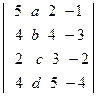 .
.
34. Решить уравнение: 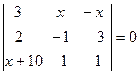 .
.
35. Вычислить определители с помощью элементарных преобразований:
а) 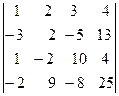 ; б)
; б) 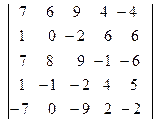 ;
;
в) 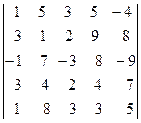 ; г)
; г) 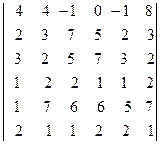 .
.
36. Найти определители диагональных матриц:
а) 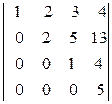 ; б)
; б) 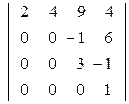 ;
;
в) 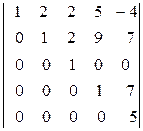 ; г)
; г) 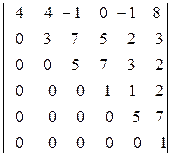 .
.
37. Вычислить с помощью элементарных преобразований определителя:
а) 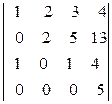 ; б)
; б) 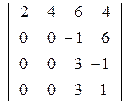 ;
;
в) 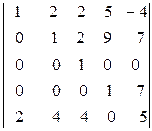 ; г)
; г) 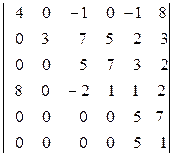 .
.
38. Вычислить определители, используя их свойства:
а) 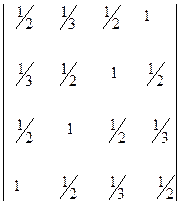 ; б)
; б) 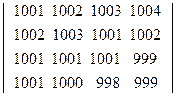 .
.
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
МЕТОД ГАУССА
Метод Гаусса заключается в последовательном исключении неизвестных. Поясним смысл метода на системе 3-х уравнений с 3-мя неизвестными.
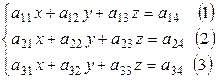 .
.
Допустим, что 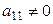 (если
(если 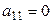 , то меняем порядок уравнений, выбрав первым такое уравнение, в котором коэффициент при x не равен нулю).
, то меняем порядок уравнений, выбрав первым такое уравнение, в котором коэффициент при x не равен нулю).
Первый шаг: делим уравнение (1) на 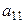 , умножаем полученное уравнение на –
, умножаем полученное уравнение на – 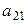 и прибавляем к (2); затем умножаем на –
и прибавляем к (2); затем умножаем на – 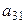 и прибавляем к (3). В результате первого шага переходим к системе
и прибавляем к (3). В результате первого шага переходим к системе
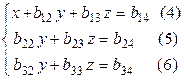 .
.
Причем 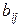 получаются из
получаются из 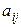 по следующим формулам:
по следующим формулам:
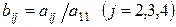
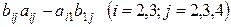 .
.
Второй шаг: поступаем с уравнениями (5), (6) точно так же, как с уравнениями (1), (2), (3) и т. д. В итоге исходная система преобразуется
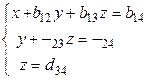
Из преобразованной системы все неизвестные определяются последовательно без труда.
Пример решения задачи.
Решить систему методом Гаусса.
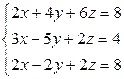
Разделим первое уравнение на 2 . Получим
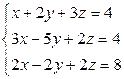 .
.
Умножаем 1-е уравнение на –3 и прибавляем ко 2-му, получаем второе уравнение в виде:
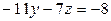 .
.
Умножая 1-е уравнение на –2 и прибавляем 3-ему, третье уравнение получаем в виде
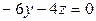 .
.
Умножим полученные уравнения на –1 и поменяем местами.
Получаем преобразованную систему уравнений. Далее действуем аналогично.
Разделим второе уравнение на 6; умножим его на –11 и прибавим к третьему.
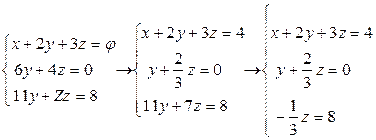 .
.
Из последней системы находим последовательно решение системы
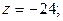
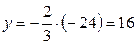
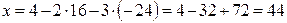 .
.
Проверка
1) 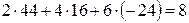 .
.
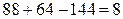 .
.
8 = 8.
2) 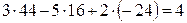 .
.
132 - 80 - 48 = 4.
4 = 4.
3) 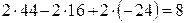 .
.
88 - 32 - 48 = 8.
8 = 8.
Ответ: x = 44; y = 16; z = - 24.
МЕТОД ЖОРДАНОВЫХ ПРЕОБРАЗОВАНИЙ
Рассмотрим систему, состоящую из 3-х уравнений с тремя неизвестными
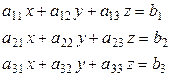 .
.
Данную систему можно представить в виде таблицы:
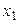 | 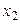 | 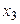 | |
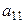 | 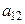 | 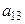 | 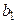 |
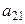 | 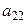 | 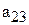 | 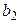 |
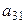 | 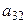 | 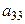 | 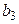 |
(1)
Выбираем любой отличный от нуля коэффициент 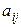 . Например,
. Например, 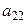 .
.
Жордановым преобразованием системы с ведущим элементом 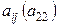 называется совокупность следующих преобразований:
называется совокупность следующих преобразований:
1) умножение i-ой строки таблицы (1) на число 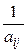 (2-й строки на
(2-й строки на 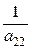 )
)
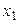 | 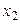 | 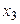 | |
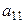 | 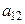 | 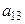 | 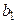 |
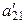 | 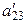 | 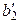 | |
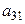 | 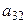 | 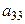 | 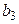 |
(2)
2) прибавление в 1-ой строке таблицы ее i-й строки (2-ой строки), умноженной на 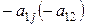 , к третьей строке ее i-й строки (2-ой строки), умноженной на
, к третьей строке ее i-й строки (2-ой строки), умноженной на 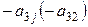 , и т. д.
, и т. д.
После этих преобразований система уравнений примет вид:
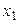 | 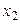 | 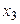 | |
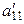 | 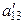 | 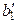 | |
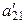 | 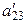 | 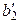 | |
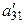 | 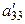 | 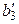 |
(3)
В результате Жорданова преобразования с ведущим элементом 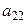 получаем систему (3), у которой неизвестное
получаем систему (3), у которой неизвестное 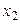 является разрешенным.
является разрешенным.
Пример. Решить систему линейных уравнений, используя Жордановы преобразования
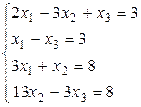 .
.
Запишем систему в виде таблицы
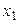 | 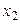 | 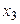 | 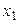 | 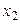 | 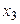 | ||||
 2 2 | -3 | -3 | |||||||
| -1 | ® | -3 | ® | ||||||
 3 3 | |||||||||
| -3 | +6 |
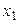 | 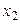 | 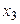 | 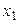 | 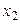 | 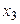 | ||||
| -1 | -1 |  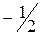 | |||||||
 ® ® | -1 | ® | 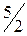 | ||||||
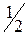 | |||||||||
Переходим к общему решению. 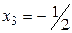 ;
; 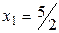 ;
; 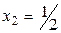 .
.
Ответ: 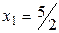 ;
; 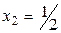 ;
; 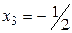 .
.
МЕТОД КРАМЕРА
Пусть дана СЛАУ третьего порядка:
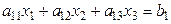
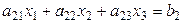
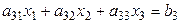 ,
,
где
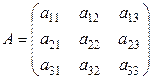
– матрица коэффициентов системы. Причем 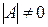 .
.
Тогда решение системы может быть найдено по формулам Крамера:
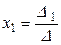 ;
; 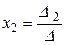 ;
; 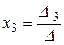 ,
,
где
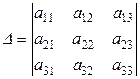
– основной определитель;
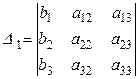 ;
; 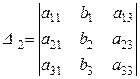 ;
; 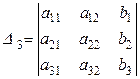
– дополнительные определители.
ОБРАТНАЯ МАТРИЦА
Квадратная матрица 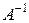 называется обратной для матрицы А, если выполняется следующее соотношение
называется обратной для матрицы А, если выполняется следующее соотношение
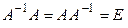 ,
,
где Е – единичная матрица.
Квадратная матрица называется невырожденной, если ее определитель отличен от 0. Если определитель матрицы равен 0, она называется вырожденной.
Всякая невырожденная матрица
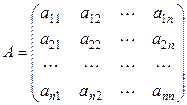
имеет обратную матрицу
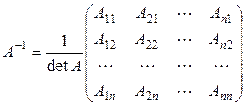 ,
,
где 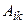 – алгебраическое дополнение элемента
– алгебраическое дополнение элемента 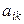 матрицы А.
матрицы А.
Чтобы найти матрицу, обратную данной, необходимо:
1) вычислить определитель данной матрицы;
2) найти алгебраические дополнения 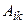 ее элементов
ее элементов 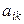 ;
;
3) составить матрицу 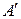 из алгебраических дополнений
из алгебраических дополнений 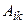 , взятых в том же порядке, что и элементы
, взятых в том же порядке, что и элементы 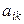 в матрице А;
в матрице А;
4) матрицу 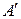 транспонировать, т. е. поменять местами строки и столбцы.
транспонировать, т. е. поменять местами строки и столбцы. 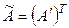 ;
;
5) каждый элемент матрицы 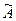 разделить на определитель матрицы А. Полученная матрица является обратной для матрицы А.
разделить на определитель матрицы А. Полученная матрица является обратной для матрицы А.
Пример выполнения задачи
Найти матрицу 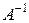 , обратную матрице А
, обратную матрице А
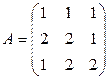 .
.
Вычислим определитель матрицы А и алгебраические дополнения ее элементов:
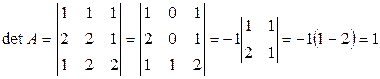 .
.
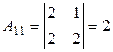 ;
; 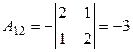 ;
; 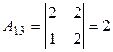 ;
;
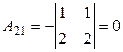 ;
; 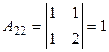 ;
; 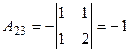 ;
;
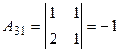 ;
; 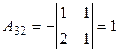 ;
; 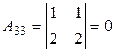 .
.
Составляем матрицы 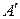 и
и 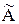 :
:
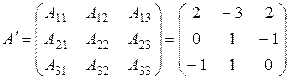 ;
;
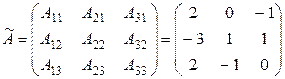 .
.
Следовательно,
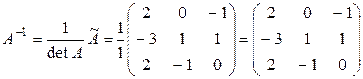 .
.
Для контроля вычислений покажем, что 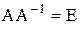 :
:
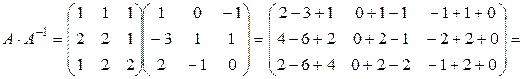
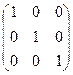 .
.
СЕМИНАР 5.
МЕТОД ГАУССА РЕШЕНИЯ СЛАУ.
МЕТОД ЖОРДАНОВЫХ ПРЕОБРАЗОВАНИЙ
Вопросы
1. Линейное уравнение.
2. Тривиальное уравнение.
3. Противоречивое уравнение.
4. Система линейных алгебраических уравнений (СЛАУ).
5. Как можно представить СЛАУ в виде расширенной матрицы.
6. Что такое решение СЛАУ.
7. Что значит «решить СЛАУ».
8. Какая СЛАУ называется несовместной.
9. Какая СЛАУ называется совместной.
10. Какая СЛАУ называется неопределенной.
11. Какая СЛАУ называется определенной.
12. Какие СЛАУ называются равносильными.
13. Какое неизвестное системы называется разрешенным.
14. Какое уравнение системы называется разрешенным.
15. Какое неизвестное системы называется свободным.
16. Какая система называется разрешенной.
17. Что называется общим решением СЛАУ.
Задачи
39. Решить с помощью метода Гаусса системы линейных алгебраических уравнений:
а) 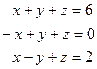 б)
б) 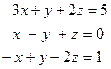
в) 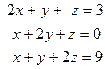 г)
г) 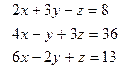
д) 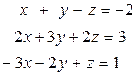 е)
е) 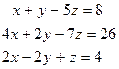
ж) 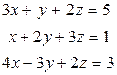 з)
з) 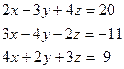


и) 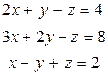 к)
к) 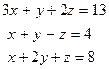
40. Найти общее решение системы с помощью метода Гаусса и одно из ее частных решений.
а) б)
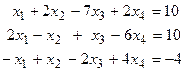
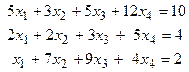
СЕМИНАР 6.
МЕТОД КРАМЕРА РЕШЕНИЯ СЛАУ.
МЕТОД ОБРАТНОЙ МАТРИЦЫ
Вопросы
1. Как выглядит матрица ступенчатого вида. Приведите схему. Какие элементы этой матрицы называются угловыми.
2. В чем суть метода Гаусса.
3. В чем заключается обратный ход метода Гаусса.
4. В чем заключается преобразование со строками матрицы системы I типа.
5. В чем заключается преобразование со строками матрицы системы II типа.
6. Какова цель жорданова преобразования СЛАУ с ведущим элементом 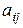 .
.
7. Сколько жордановых преобразований можно сделать с расширенной матрицей системы.
8. Формулы Крамера для решения системы 3-х линейных уравнений.
9. Когда можно найти решение СЛАУ по формулам Крамера.
10. Формула для нахождения обратной матрицы.
11. Как записать СЛАУ в векторно-матричной форме.
12. Формула для нахождения решения СЛАУ с помощью обратной матрицы.
Задачи
41. Проверить, совместна ли система, и решить ее методом Крамера.
а) 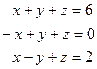 б)
б) 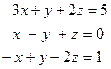 в)
в) 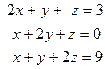
г) 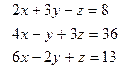 д)
д) 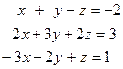 е)
е) 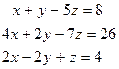
42. Найти обратную матрицу, используя формулу.
а) б) в)
А= 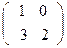 А=
А= 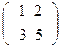 А=
А= 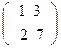
г) д) е)
А= 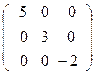 А=
А= 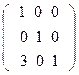 А=
А= 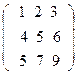
ж) з) и)
А= 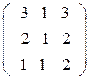 А=
А= 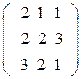 А=
А= 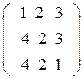
к) л) м)
А= 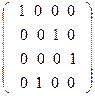 А=
А= 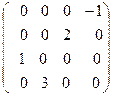 А=
А= 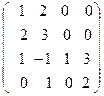
43. Решить с помощью обратной матрицы определенную систему линейных алгебраических уравнений, представленную своей расширенной матрицей.
а) 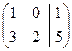 б)
б) 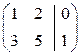 в)
в) 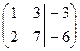
г) 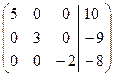 д)
д) 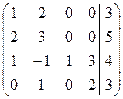
Примечание: воспользоваться решением предыдущего номера.
СЕМИНАР 7.
