Матрицы. операции над матрицами
Вопросы
1. Определение матрицы размерности m x n
2. Определение квадратной матрицы.
3. Что такое матрица-строка.
4. Что такое матрица-столбец.
5. Как умножить матрицу на число.
6. Что такое нулевая матрица.
7. Свойства умножения матрицы на число.
8. Как найти сумму матриц.
9. Свойства сложения матриц.
10. Какие матрицы называются равными.
11. Какая матрица называется противоположной к матрице А.
12. Какие матрицы можно перемножать.
13. Если матрицы А и В можно перемножать, то как получаться элементы матрицы С=АВ (элемент стоящий в i-ой строке и j-ом столбце).
14. Свойства умножения матриц.
15. Какая матрица называется транспонированной к матрице А.
16. Какая матрица называется диагональной.
17. Какая матрица называется единичной. Основное свойство единичной матрицы.
18. В чем заключается элементарное преобразование I типа над строками матрицы.
19. В чем заключается элементарное преобразование II типа над строками матрицы.
20. Как выглядит матрица ступенчатого вида.
Задачи
17. Найти сумму матриц А и В:
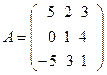 ,
, 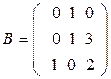 .
.
Определить размерность матриц.
18. Умножить матрицу Ана числоk:
а) 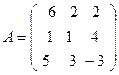 , k = 3; б)
, k = 3; б) 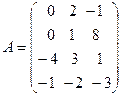 , k = –1.
, k = –1.
Определить размерность матриц.
19. Выполнить действия:
а) 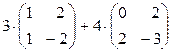 б)
б) 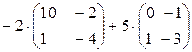
20. Найти линейные комбинации матриц 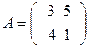 и
и 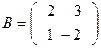 :
:
а) 2А + 5В; б) –2А + 4В; в) 3А – 2В; г) –А–2В.
21. Перемножить матрицы, если это возможно:
а) 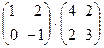 ; б)
; б) 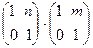 ;
;
в) 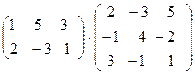 ; г)
; г) 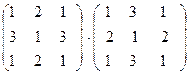 .
.
22. Выполнить действия:
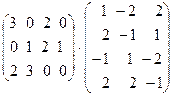 +
+ 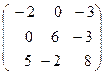 .
.
23. Вычислить степени матрицы А:
а) 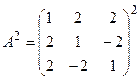 ; б)
; б) 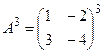 ;
;
в) 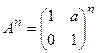 ; г)
; г) 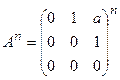 .
.
24. Найти значение матричного многочлена: 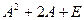 , где
, где
а) 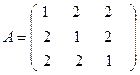 ; б)
; б) 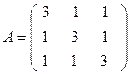 .
.
25. Произвести умножение строки А на матрицу В:
а) 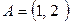 ,
, 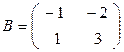 ;
;
б) 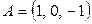 ,
, 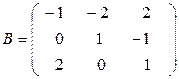 ;
;
в) 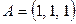 ,
, 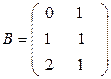 ;
;
г) 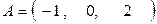 ,
, 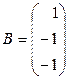 .
.
26. Произвести умножение матрицы А на столбец В:
а) 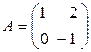 ,
, 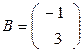 ;
;
б) 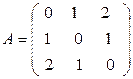 ,
, 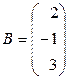 ;
;
в) 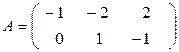 ,
, 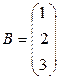 ;
;
г) 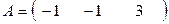 ,
, 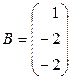 .
.
27. Решить систему матричных уравнений:
а) 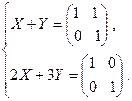 ; б)
; б) 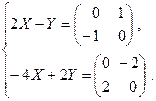 .
.
28. Решить матричные уравнения:
а) 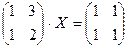 ; б)
; б) 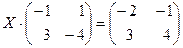 ;
;
в) 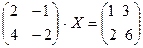 ; г)
; г) 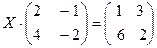 .
.
ОПРЕДЕЛИТЕЛИ И ИХ СВОЙСТВА
Определителем квадратной матрицы 2-го порядка называется число
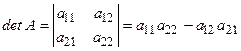 .
.
Определителем квадратной матрицы 3-го порядка называется 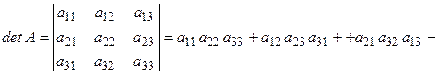
 .
.
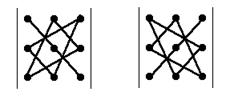
Существует удобная схема для вычисления определителя третьего порядка (рис. 1, 2).
По схеме, приведенной на рис. 1, произведение соединенных элементов берется со знаком плюс, а по схеме рис. 2 - со знаком минус.
+ –
рис. 1 рис. 2
Минором элемента 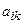 определителя матрицы А называется определитель, полученный из исходной матрицы вычеркиванием i-ой строки и k-ого столбца. Минор элемента
определителя матрицы А называется определитель, полученный из исходной матрицы вычеркиванием i-ой строки и k-ого столбца. Минор элемента 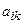 обозначают
обозначают 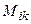 .
.
Алгебраическим дополнением элемента 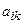 определителя матрицы А называется ее минор, умноженный на
определителя матрицы А называется ее минор, умноженный на 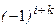 . Алгебраическое дополнение элемента
. Алгебраическое дополнение элемента 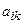 будем обозначать
будем обозначать 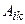 . В соответствии с определением
. В соответствии с определением 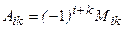 .
.
Теорема разложения
Определитель любого порядка равен сумме произведений элементов некоторой его строки (столбца) на их алгебраические дополнения.
Свойства определителей
1. Определитель не изменяется при транспонировании матрицы.
2. При перестановке двух строк (столбцов) определитель меняет знак на противоположный.
3. Определитель равен нулю, если все элементы некоторой строки (столбца) равны нулю.
4. Определитель с двумя одинаковыми строками (столбцами) равен нулю.
5. Определитель с двумя пропорциональными строками (столбцами) равен нулю.
6. Множитель, общий для всех элементов некоторой строки (столбца), можно вынести за знак определителя.
7. Определитель не изменится, если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), предварительно умножив их на одно и то же число.
Пример.Вычислить определитель 4-го порядка
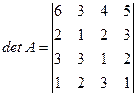 .
.
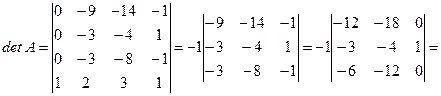
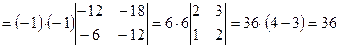 .
.
(1‑ый определитель 4-го порядка получен из исходного умножением 4‑ой строки поочередно на -6, -2, -3 и прибавлением ее соответственно к 1-ой, 2-ой, 3-ей строкам).
СЕМИНАР 4.
