С классическим вариационным исчислением

С помощью принципа максимума можно вывести необходимые условия существования экстремума в задачах вариационного исчисления. Рассмотрим динамическую управляемую систему с функционалом

.

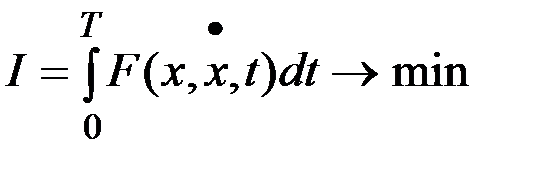Пусть 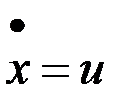, т.е. управляющие параметры есть скорости изменения фазовых координат. Применим принцип максимума.

Составим гамильтониан: 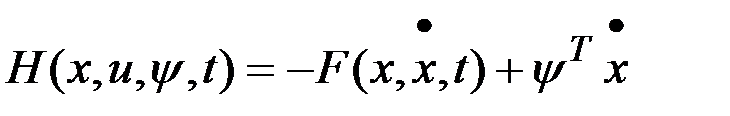. Используем необходимое условие максимума гамильтониана:

, .

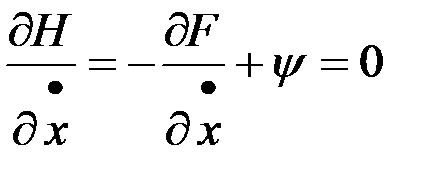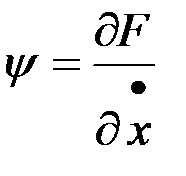Продифференцируем выражение для по времени:

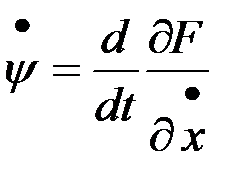
Согласно канонического уравнения для сопряженных переменных

.

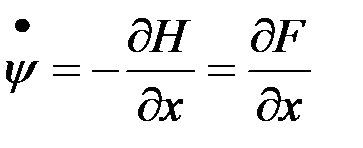Сопоставляя два последних выражения, получим уравнение Эйлера

.

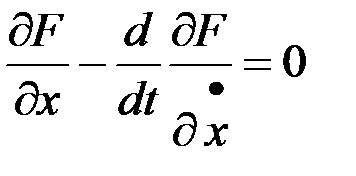Условие второго порядка для существования максимума функции Гамильтона определяется как условие отрицательной определенности матрицы вторых частных производных гамильтониана, т.е. матрицы 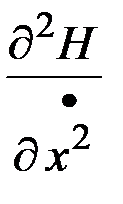. Из этого условия следует условие положительной определенности матрицы 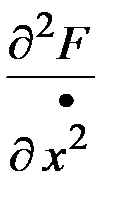, или 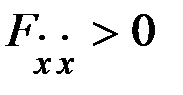, т.е. условие Лежандра.

Согласно принципу максимума, если 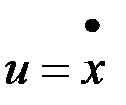является оптимальным управлением, то при любом другом управлении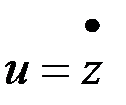

.

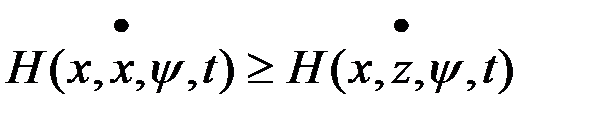Учитывая выражение для гамильтониана, получаем неравенство:

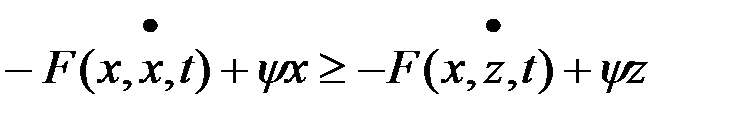, или

,

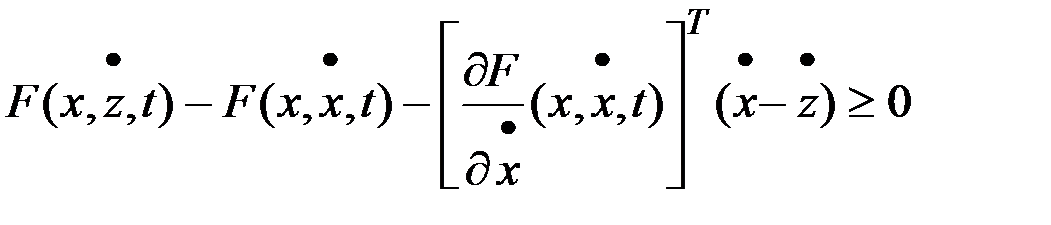которое есть условие Вейерштрасса.

Таким образом, с помощью принципа максимума получены необходимые условия экстремума в задачах классического вариационного исчисления.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

Принцип оптимальности Беллмана.

Уравнение Беллмана

В основе метода динамического программирования лежит принцип оптимальности, сформулированный Р.Беллманом: оптимальный процесс обладает тем свойством, что каким бы ни было начальное управление последующее управление должно быть оптимальным по отношению к состоянию, происходящему от начального управления.

Предположим, что 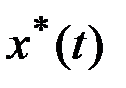- оптимальная траектория, приводящая систему из начального состояния 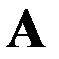в конечное , промежуточное состояние 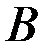соответствует моменту времени 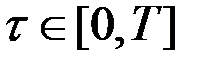(рис.4.1). Согласно принципу оптимальности Беллмана участок траектории 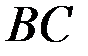представляет собой оптимальную траекторию по отношению к начальному состоянию 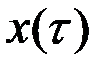, т.е. оптимальное управление на участке 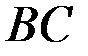не зависит от того, каким образом система приведена в состояние .

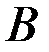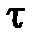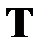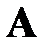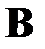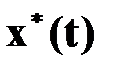Рис.4.1. Оптимальная траектория

Другими словами, каждый участок оптимальной траектории является оптимальной траекторией относительно своей начальной точки, оптимальное управление не зависит от предыстории движения системы и для будущих моментов времени определяется только состоянием в данный момент. Таким образом, всю траекторию движения системы можно разбить на части, двигаясь от ее конца к началу, и оптимизировать движение по частям.

Рассмотрим задачу оптимального управления динамической системой:

, , , , , ,

.

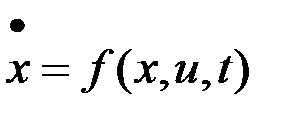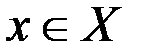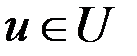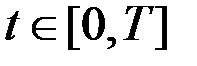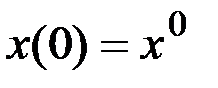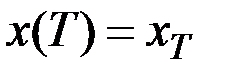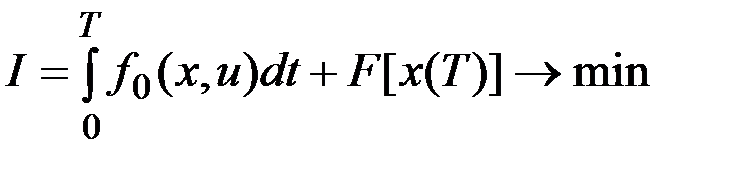Требуется синтезировать закон оптимального управления .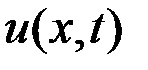

Пусть поставленная задача решена. Введем обозначение: 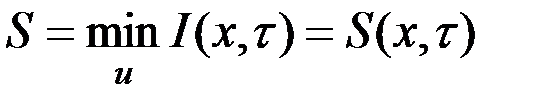- минимальное значение функционала для участка траектории , тогда 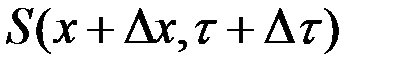- есть минимальное значение функционала 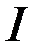для измененного относительно 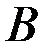состояния и времени. Очевидно, что 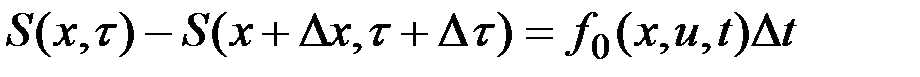. Тогда в общем случае независимых изменений состояния и времени получим в соответствии с принципом оптимальности Беллмана

.

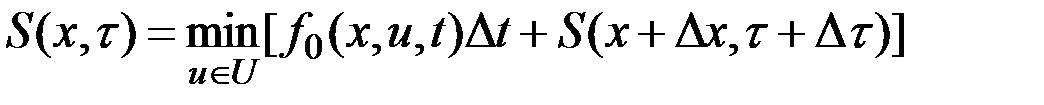Введем допущения о том, что функция 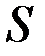непрерывна и непрерывно дифференцируема (во многих задачах эти условия не выполняются). Разложим 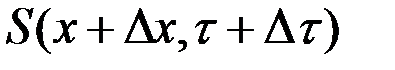в ряд Тейлора, отбросив малые величины, получим

.

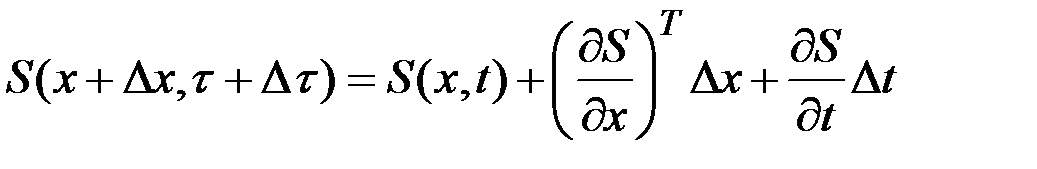Подставив в предыдущее выражение, получим

.

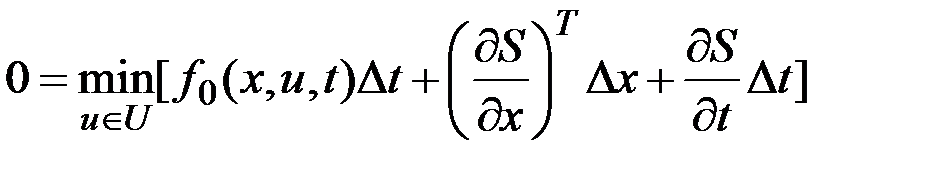Разделив на 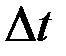, при 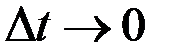получим

.

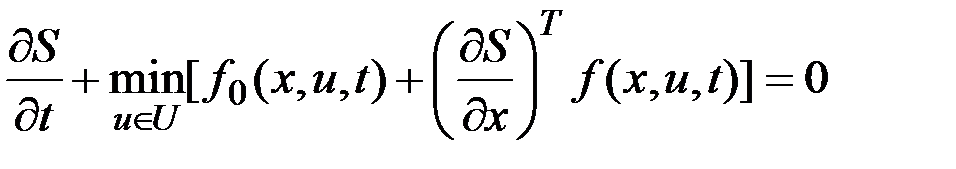Полученное нелинейное дифференциальное уравнение в частных производных относительно функции 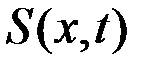называется уравнением Беллмана. При решении конкретных задач аналитическое решение можно получить лишь в некоторых частных случаях. В общем случае уравнение Беллмана решается численно.

Функция 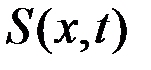есть функция текущего состояния системы, ее принято называть функцией будущих потерь или функцией Беллмана. Она является мерой стоимости перехода из точки с координатами 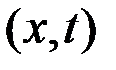в точку с координатами 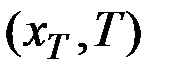. В задаче Больца функция будущих потерь в конечный момент времени равна терминальному члену, т.е. 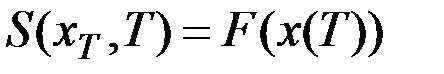, в задаче Лагранжа 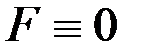, следовательно, 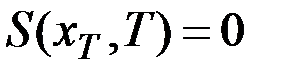. Эти выражения задают граничные условия для уравнения Беллмана.