Доверительный интервал для оценки среднего квадратического отклонения нормального распределения
Если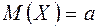 
неизвестно, то доверительный интервал для оценки 
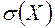имеет вид:
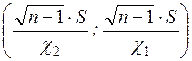
где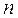 
- объем выборки; 
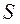- исправленное среднее квадратическое отклонение:
, 
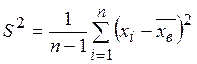
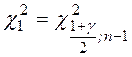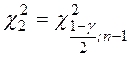– квантили 
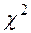– распределения, определяемые по таблице 
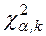([1], Приложение 5)
при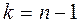 
и 
, 
.
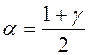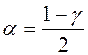Пример.Для оценки параметра 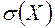нормально распределенной случайной величины была сделана выборка объема в 25 единиц и вычислено 
.
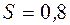Найти доверительный интервал, покрывающий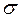 
с вероятностью 
.
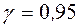Имеем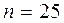 
, .
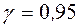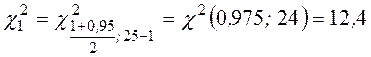
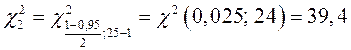
Доверительный интервал имеет вид:
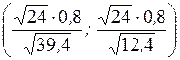или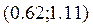 
.
2. Другой вид доверительного интервала для оценки 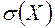нормального распределения имеет вид:
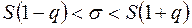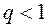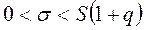при 
;
при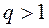 
;
где 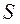- исправленное среднее квадратическое отклонение;
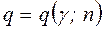находим по таблице значений ([1], Приложение 4).
Пример.Для оценки параметра нормально распределенной случайной величины была сделана выборка объема в 25 единиц и вычислено .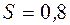
Найти доверительный интервал, покрывающий 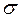с вероятностью .
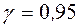Имеем , ,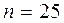 
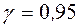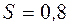
По таблице значений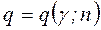 
находим 
.
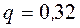Доверительный интервал имеет вид:
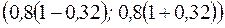или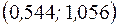 
.
Замечание. Доверительные интервалы в примерах 8 и 9 получили разные при одинаковых данных, но они с вероятностью 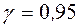покрывают среднее квадратическое отклонение 
.
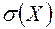Типовые задачи
Дан статистический ряд нормально распределенной случайной величины Х, где х – масса тушек бройлера.
| xi | 1,7 | 1,5 | 1,2 | 1,8 | 1,6 | 1,4 | 0,9 | |
| fi |
Найти: среднее арифметическое; среднее квадратическое; моду; медиану; размах вариации; дисперсию; среднее квадратическое отклонение; коэффициент вариации.
Построить полигон распределения, гистограмму и кумуляту.
Решение
xi – конкретное значение признака X.
fi – число единиц (частоты) совокупности с данным значением признака(частот).
1. Для нахождения числовых характеристик необходимо ранжировать ряд (по возрастанию).
Ранжируем ряд:
0,9 0,9 0,9 1,2 1,2 1,2 1,4 1,4 1,4 1,4 1,4 1,5 1,5 1,6 1,6 1,6 1,6 1,6 1,6 1,6 1,7 1,7 1,7 1,7 1,7 1,8 1,8 1,8 1,8 1,8 1,8 2,0
2. Составим Табл.1 и будем вносить в неё данные по мере выполнения необходимых расчетов (выполним округление до второго знака после запятой).
Табл. 1
 |  |  |  |  |  |  |
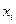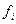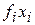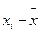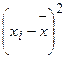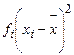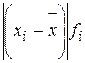| 0,9 | 2,7 | -0,62 | 0,38 | 1,14 | 1,86 | |
| 1,2 | 3,6 | -0,32 | 0,10 | 0,3 | 0,96 | |
| 1,4 | -0,12 | 0,01 | 0,05 | 0,6 | ||
| 1,5 | -0,02 | 0,0004 | 0,0008 | 0,04 | ||
| 1,6 | 11,2 | 0,08 | 0,006 | 0,04 | 0,56 | |
| 1,7 | 8,5 | 0,18 | 0,03 | 0,15 | 0,9 | |
| 1,8 | 10,8 | 0,28 | 0,08 | 0,48 | 1,68 | |
| 2,0 | 0,48 | 0,23 | 0,23 | 0,48 | ||
| Сумма | 48,8 | 2,39 | 7,08 |
Числа, показывающие, сколько раз отдельные варианты встречаются в данной совокупности – частотывариант f.
Общая сумма частот вариационного ряда равна объему данной совокупности
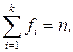
где k – число групп; n – общее число наблюдений, или объем совокупности.
3. Необходимо определить вариацию средней массы тушек бройлера по всей совокупности. Вариация массы тушек бройлера определяется с помощью средней арифметической.
Получим:
= 
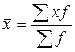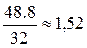
Средняя масса тушек бройлера составляет 1,52 кг.
4. Для измерения вариации применяют различные показатели, из которых основными являются размах вариации (лимит), среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Размах вариации определяется как разница между наибольшим и наименьшим значениями признака.
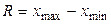
где xmin, xmax- минимальное и максимальное значение признака.
Получим:
R = 2,0 – 0,9 = 1,1
xmin = 0,9
xmax = 2,0
Среднее линейное отклонение - средняя арифметическая из абсолютных отклонений отдельных вариант от средней арифметической: