Свойства вероятностей. Условная вероятность. Независимость событий. Теоремы сложения и умножения вероятностей
Пусть для некоторого случайного эксперимента построено вероятностное пространство (Ω,F,P).
Случайным событием А называется любое подмножество пространства элементарных событий Ω. Событие 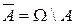 называется противоположным событию А; событие
называется противоположным событию А; событие 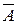 означает, что событие А не произошло. События А и В называются несовместимыми, если их совместное появление (произведение) – невозможное событие: АВ=Ø. События А1,А2,...,Ат образуют полную группу событий, если они попарно несовместны и их объединение является достоверным событием:
означает, что событие А не произошло. События А и В называются несовместимыми, если их совместное появление (произведение) – невозможное событие: АВ=Ø. События А1,А2,...,Ат образуют полную группу событий, если они попарно несовместны и их объединение является достоверным событием:
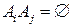 , при i¹j;
, при i¹j; 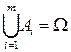 .
.
Числовая неотрицательная функция Р,определенная на F,удовлетворяет следующим свойствам:
1. Если события А1,А2,...,Аm образуют полную группу событий, товероятность объединения этих событий равна единице:
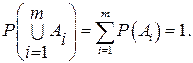
2. Вероятность противоположного события: Р( 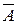 )= 1–Р(А).
)= 1–Р(А).
3. Если событие А влечет за собой событие В, то вероятность события А не превосходит вероятности события В, т.е. Р(А) 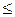 Р(В).
Р(В).
Пусть А и В – наблюдаемые события в эксперименте, причем Р(А)>0 (P(B)>0). Условной вероятностью Р(В|А) (P(A|B)) осуществления события В (A) при условии, что событие А (B) произошло в результате данного эксперимента, называется величина, определяемая равенством:
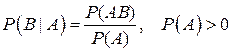 или
или 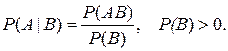 (2.1)
(2.1)
Из этих формул следует, что
P(AB)=P(A)P(B|A) или P(AB)=P(B)P(A|B).(2.2)
Теорема сложения:
Пусть А1,А2,...,Аm – совместные события. Тогда вероятность их объединения вычисляется по формуле:
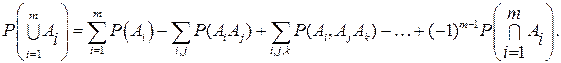 (2.3)
(2.3)
Для двух событий эта формула имеет вид:
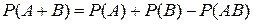 . (2.4)
. (2.4)
Событие А называется независимым от события В, удовлетворяющего условию Р(В)>0, если выполняется равенство: P(A|B)=P(A).
События А и В называются независимыми,если:
P(AB)=P(A)P(B). (2.5)
События А1,А2,...,Ап называются независимыми в совокупности, если для любого набора из т событий (т=2,3,...,п) выполняется равенство:
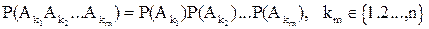 . (2.6)
. (2.6)
Теорема умножения :
Вероятность произведения событий А1,А2,...,Аm равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется в предположении, что все предыдущие имели место:
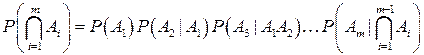 . (2.7)
. (2.7)
Для независимых событий в совокупности формула (2.7) принимает вид:
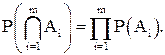 (2.8)
(2.8)
Заметим, что при использовании свойств и теорем теории вероятностей пространство элементарных событий строить не обязательно.
Задачи.
2.1. Вероятность заключить контракт с некоторой фирмой равна 0,5, а вероятность заключить контракт на сумму 1млн.ден.ед. равна 0,2. Найти вероятность того, что при заключении контракта его сумма 1 млн.ден.ед.
Решение: Для описания эксперимента, рассматриваемого в задаче введем следующие события: А={заключен контракт с некоторой фирмой}, В={сумма контракта равна 1 млн.ден.ед.}. Событие АВ={заключен контракт на сумму 1млн.ден.ед.}. Событие В|А={сумма контракта при условии, что он заключен, равна 1млн.ден.ед.}. Вероятность событий А и АВ: Р(А)=0,5; Р(АВ)=0,2. Тогда по формуле (2.1) вероятность искомого события равна:
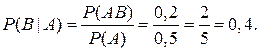
Ответ: Вероятность того, что сумма контракта при его заключении 1 млн.ден.ед. равна 0,4.
2.2.В семье двое детей. Считая, что рождение мальчика и девочки – независимые и равновероятные события, вычислить вероятность того, что оба ребенка – девочки, если известно, что в семье есть девочка.
2.3.Пусть события А и В зависимы. Следует из этого, что они несовместимы? Независимы?
2.4.Пусть события А и В несовместимы. Будут ли они зависимыми? Независимыми?
2.5.Из 100 претендентов на должность менеджера внешнеторговой фирмы 50 человек знают английский язык, 40 – французский и 35 – немецкий. Английский и французский языки знают 20 претендентов, английский и немецкий – 8, французский и немецкий – 10. Все три языка знают 5 претендентов. Один из претендентов зашел на собеседование. Рассмотрим события: А={вошедший знает английский язык}; В={вошедший знает французский язык}; С={вошедший знает немецкий язык}; D={вошедший знает английский или французский языки}; Е={вошедший не знает ни одного языка}. Требуется: а) указать все пары независимых событий; б) установить, являются ли события А,В,С независимыми в совокупности; в) вычислить вероятности событий D и Е.
Решение: Так как рассматриваемый эксперимент состоит в случайном выборе претендента, то пространство элементарных исходов Ω можно записать в виде: 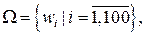 wi – выбор одного i-го претендента. Отсюда следует, что n(Ω)=100. События, приведенные в задаче, имеют следующий состав:
wi – выбор одного i-го претендента. Отсюда следует, что n(Ω)=100. События, приведенные в задаче, имеют следующий состав:
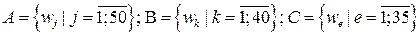 , индексы j, k, e – изменяются независимо друг от друга; D=А+В;
, индексы j, k, e – изменяются независимо друг от друга; D=А+В; 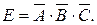 Воспользовавшись классическим определением вероятности, определим вероятности событий А, В, С, АВ, АС, ВС:
Воспользовавшись классическим определением вероятности, определим вероятности событий А, В, С, АВ, АС, ВС:
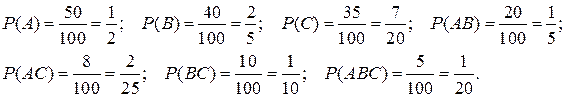
a) Для ответа на вопрос проверим равенства (2.2):
1) P(AB)=P(A)∙P(B); 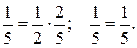 Следовательно события А и В независимы;
Следовательно события А и В независимы;
2) P(ВС)=P(В)∙P(С); 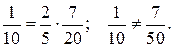 Следовательно события Ви С не являются независимыми.
Следовательно события Ви С не являются независимыми.
3) P(AС)=P(A)P(С); 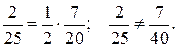 Следовательно события А и С не являются независимыми.
Следовательно события А и С не являются независимыми.
б) Из приведенных вычислений следует, что для любых двух событий из совокупности событий А,В,С не выполняется равенство (2.6), то события А, В и С не являются независимыми в совокупности.
в) Поскольку события А и В совместны и D=А+В, то, воспользовавшись формулой (2.4), получим:
P(D)=P(A)+P(B)-P(AB)= 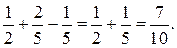
Легко показать, что 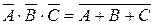 . Тогда, воспользовавшись свойством 2 и формулой (2.3) для трех событий, будем иметь:
. Тогда, воспользовавшись свойством 2 и формулой (2.3) для трех событий, будем иметь:
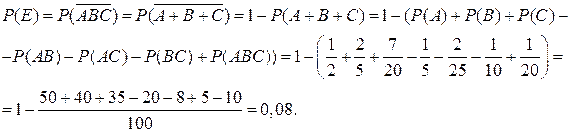
2.6.В читальном зале имеется 6 учебников по теории вероятностей, из которых 3 в твердом переплете. Библиотекарь наудачу взял 2 учебника. Найти вероятность того, что оба учебника окажутся в твердом переплете.
Решение: Пусть А – первый взятый учебник имеет твердый переплет, В – второй учебник имеет твердый переплет. Вероятность того, что первый учебник имеет переплет 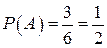 . Вероятность того, что второй учебник имеет твердый переплет, при условии, что первый взятый учебник был в переплете, т.е. условная вероятность события В равна:
. Вероятность того, что второй учебник имеет твердый переплет, при условии, что первый взятый учебник был в переплете, т.е. условная вероятность события В равна: 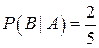 .
.
Искомая вероятность того, что оба учебника имеют переплет, по теореме умножения вероятностей зависимых событий равна
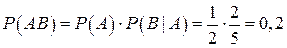 .
.
Ответ: Р=0,2.
2.7.Найти вероятность того, что наудачу взятое двухзначное число окажется кратным 2, либо 5, либо тому и другому одновременно.
2.8.В продукции часового завода брак составляет 5% от общего количества выпускаемых часов. Для контроля отобрано 20 часов. Какова вероятность того, что среди них имеются хотя бы одни часы с браком?
2.9.В цехе работают 7 мужчин и 3 женщины. По табельным номерам наудачу отобраны 3 человека. Найти вероятность того, что все отобранные лица окажутся мужчинами.
2.10.Бухгалтер составил два варианта годового баланса предприятия. Вероятность того, что в первом варианте баланса содержится ошибка 0,85, а во втором – 0,99. Найти вероятность того, что баланс предприятия составлен с ошибкой.
2.11.Вероятности попадания в цель при стрельбе из трех орудий соответственно равны: 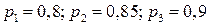 . Какова вероятность хотя бы одного попадания при одном залпе из трех орудий?
. Какова вероятность хотя бы одного попадания при одном залпе из трех орудий?
Решение: Введем следующие события: А={хотя бы одно попадание при одном залпе}, Ai={попадание i-го орудия}, i=1,2,3, 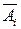 ={промах i-го орудия}. События
={промах i-го орудия}. События 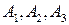 независимы в совокупности, но совместны. Вероятности противоположных событий равны:
независимы в совокупности, но совместны. Вероятности противоположных событий равны:
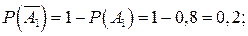
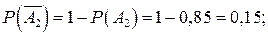
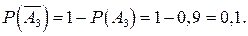
Так как событие А противоположно событию, состоящему в том, что все три орудия промахнулись, то
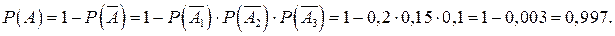
Ответ: р=0,997.
2.12.Студент Иванов подписал поздравительные открытки трем девушкам, запечатав их в конверты, и случайным образом подписал адреса. Определить вероятность того, что хотя бы одна открытка попадет по назначению.
2.13.В коробке лежит 3 буквы разрезной азбуки: буква «М», две буквы «И», четыре буквы «Р». Извлекаем подряд 3 карточки из коробки без возвращения. Определить вероятность того, что в результате извлечения букв образуется слово «МИР».
2.14.Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором три вопроса.
2.15.Цех производит кинескопы для телевизоров, причем 30% всех кинескопов имеют диагональ 51 см, а 70% – 72 см. Известно, что 50% всей продукции отправляется на экспорт, причем из общего числа кинескопов с диагональю 72 см 40% отправляется на экспорт. Найти вероятность того, что наудачу взятый кинескоп имеет диагональ 51 см и будет отправлен на экспорт.
2.16.Студент может уехать в университет или автобусом, интервал движения которого 20 минут, или троллейбусом, интервал движения которого 10 минут. Найти вероятность того, что студент, подошедший к остановке, уедет в течение ближайших пяти минут.
2.17.На распродаже к некоторому моменту времени осталось: 1 пара мужской обуви; 2 пары детской и 3 пары женской обуви. Каждый очередной покупатель с равной вероятностью покупает лишь одну пару обуви. Два человека из очереди последовательно приобрели обувь. Найти вероятность того, что а) куплена разная обувь; б) куплена детская или женская обувь.
2.18.Вероятность того, что в течение полугода цены на товары народного потребления увеличатся, равна 0,95, а вероятность того, что за этот же промежуток времени изменится (увеличится) минимальная заработная плата, равна 0,9. Найти вероятность появления только одного из этих событий, если они независимы.
2.19.На рынке 7 фирм продают средства производства, а 3 фирмы – предметы потребления. Покупатель наудачу заключает сделки с тремя фирмами. Найти вероятность того, что все отобранные фирмы представляют средства производства.
2.20.Определить вероятность того, что выбранное наудачу изделие является первосортным, если известно, что 5% всей продукции является бракованной, а 85% не бракованных изделий удовлетворяет требованиям первого сорта.
2.21.Бухгалтер обслуживает 5 отделов. 20% рабочего времени он проводит в первом отделе, 10% – во втором, 15% – в третьем, 25% – в четвертом и, наконец, 30% – в пятом. Найти вероятность того, что в наудачу выбранный момент времени бухгалтер находится: а) в первом или третьем отделе; б) во втором или пятом; в) в первом или четвертом; г) в первом или втором, или третьем; д) в четвертом или пятом.
2.22.Акционерное общество состоит из трех независимых заводов, работающих в течение времени Т без убытков соответственно с вероятностями 0,851, 0,751 и 0,701. Найти вероятность того, что за время Т с убытками будет работать: а) только один завод; б) хотя бы один завод.
2.23.Завод содержит 2 одинаковых параллельных цеха, дублирующих друг друга. Вероятность безотказной работыкаждого цеха равна 0,9. При выходе из строя первого цеха осуществляется мгновенное переключение с вероятностью, равной 1, на второй цех. Определить вероятность работы завода.
2.24.Завод состоит из трех цехов. Для того, чтобы завод остановился, необходимо и достаточно, чтобы остановились и первый и второй цеха или только третий цех. Цеха останавливаются независимо друг от друга , причем вероятности остановки цехов за определенный промежуток времени соответственно равны 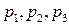 . Определить вероятность того, что завод не выйдет из строя за указанный промежуток времени.
. Определить вероятность того, что завод не выйдет из строя за указанный промежуток времени.
2.25.Вероятность снижения налога на корпорации в этом году оценивают в 0,5, а вероятность того, что наш основной конкурент не внесет изменений в важнейшее изделие – в 0,3, причем оба эти события рассматриваются как независимые друг от друга. Определить вероятность появления обоих исходов.
2.26.Известны следующие значения вероятности дополнительных потребностей фирмы в инженерах на предстоящие два года:
| Число инженеров | <100 | 100–199 | 200–299 | 300–399 | 400–499 | ≥500 |
| Вероятность | 0,1 | 0,15 | 0,3 | 0,1 | 0,05 |
а) Какова вероятность того, что на протяжении двух предстоящих лет фирме дополнительно требуется 400 и более инженеров.
б) Какова вероятность того, что фирме потребуется, по меньшей мере, 200, но не более 399 инженеров?
2.27.На протяжении некоторого периода цены двух третей котирующихся на бирже акций повышались или оставались неизмененными, а цены одной трети акций падали. Предположим, что проводится исследование цен трех наугад выбранных акций.
а) Обозначая повышение цены акции или ее неизменность через А, а падение цены через В, постройте древовидную диаграмму вероятностей повышения или падения цен для выборки из трех акций (диаграмма должна быть трехступенчатой).
б) Пользуясь этой диаграммой, определите вероятность падения цен всех трех акций.
в) Какова вероятность падения цены, по крайней мере, одной акции. (Только одна ветвь диаграммы не удовлетворяет этому условию; поэтому для получения ответа из 1,0 можно вычесть вероятность трех последовательных исходов, представленных на этой ветви).
2.28.Вероятность увеличения потребительского спроса на изделия нашей фирмы в будущем году оценивают в 0,7. Если эта оценка оправдается, то с вероятностью с 0,8 возрастет объем продаж фирмы. Если же она не оправдается, то вероятность расширения продаж составит 0,5.
а) Какова вероятность роста потребительского спроса и объема продаж?
б) Какова вероятность ситуации, при которой нет одновременного увеличения, как потребительского спроса, так и объема продаж.
2.29.За некоторый промежуток времени торговая фирма может быть ликвидирована с вероятностью 0,25, работать с прибылью с вероятностью 0,25 и разделиться на две фирмы по группам товаров с вероятностью 0,5. В следующий такой же промежуток времени с каждой торговой фирмой независимо от ее регистрации происходит то же самое. Сколько фирм и с какими вероятностями могут работать к концу второго промежутка времени?
2.30.Пусть событие А в каждом испытании появляется с вероятностью р и производится п испытаний. Как вычислить вероятность того, что событие А появится хотя бы один раз в п испытаниях (ответ обосновать).
Решение: Искомая вероятность 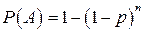 .«Хотя бы один раз» – это значит, что событие не произойдет ни разу – (1-р)п.Тогда искомая вероятность – это вероятность противоположного события.
.«Хотя бы один раз» – это значит, что событие не произойдет ни разу – (1-р)п.Тогда искомая вероятность – это вероятность противоположного события.
2.31.В продукции завода брак составляет 3% от общего количества выпускаемых деталей. Для контроля отобрано 10 деталей. Определить вероятность того, что среди отобранных деталей имеется хотя бы одна бракованная.
2.32.На ярмарке п предпринимателей продают одну и ту же продукцию. Вероятность продать всю продукцию любым предпринимателем равна 0,8. Найти вероятность того, что хотя бы один из них продаст всю продукцию.
2.33.На бирже два брокера соревнуются, кто на большую сумму заключит сделок. Причем для этого необходимо первому заключить т сделок, а второму – п сделок (m>n). Вероятность заключить следующую сделку для первого брокера равна р, а для второго q=1-p. Определить вероятность победить в этом соревновании первым брокером.
