Элементы теории корреляции .

Теория корреляции изучает связь между несколькими признаками и выявляет направление и тесноту этой связи, а так же позволяет строить модели исследуемых процессов и составлять прогнозы протекания этих процессов.

Во многих задачах требуется установить и оценить зависимость изучаемой случайной величины Y от случайной величины X.

Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой. В этом случае статистическую зависимость называют корреляционной.

Корреляционная зависимость может быть двух типов: линейной и криволинейной.

Рассмотрим более подробно линейную корреляционную зависимость.

Линейная корреляционная зависимость (корреляция) между признаками Х и У выражается уравнением вида:

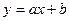
Такое уравнение называется уравнением регрессии У на Х, а соответствующая прямая – выборочной линией регрессии.

Неизвестные параметры 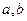находят из системы уравнений

.

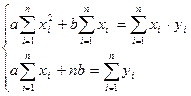Уравнение корреляционной зависимости можно получить из уравнения вида

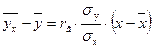
где , , , , , .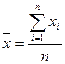

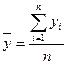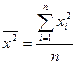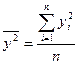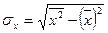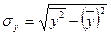Коэффициент корреляции ( 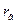) показывает тесноту связи и направления между признаками 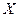и .

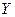Свойства коэффициента корреляции:

1.

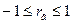
2. Если 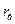= 1, то зависимость между признаками Х и У является функциональной

3. Если 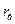= 0, то признаки Х и У не связаны линейной корреляционной зависимостью, но зависимость может иметь криволинейный характер.

С увеличением 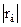связь между признаками Х и У становится теснее.

При 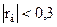- зависимость между признаками слабая, при 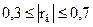- средняя, при 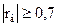- сильная.

Если 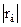положителен, то связь между признаками прямая, если 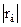отрицателен – обратная.

Коэффициент корреляции вычисляется по формуле

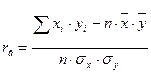
Простейшим визуальным способом выявить наличие взаимосвязи между количественными переменными является построение диаграммы рассеяния. Это график, на котором по горизонтальной оси (X) откладывается одна переменная, по вертикальной (Y) другая. Каждому объекту на диаграмме соответствует точка, координаты которой равняются значениям пары выбранных для анализа переменных.

Выборочной линией регрессии Y на X называется график функции .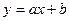

Пример 1. Для выявления корреляционной зависимости оптической плотности Y раствора от концентрации Х растворенного вещества было проведено 10 опытов. Их результаты приведены в таблице.

xi
yi

Полагая, что между признаками X и Y имеет место линейная корреляционная связь, определите выборочное уравнение линейной регрессии и выборочный коэффициент линейной корреляции. Постройте диаграмму рассеяния и линию регрессии. Сделайте вывод о направлении и тесноте связи между X и Y. Используя полученное уравнение линейной регрессии, оцените ожидаемое среднее значение признака Y, при X₀ = 55%.

Решение.

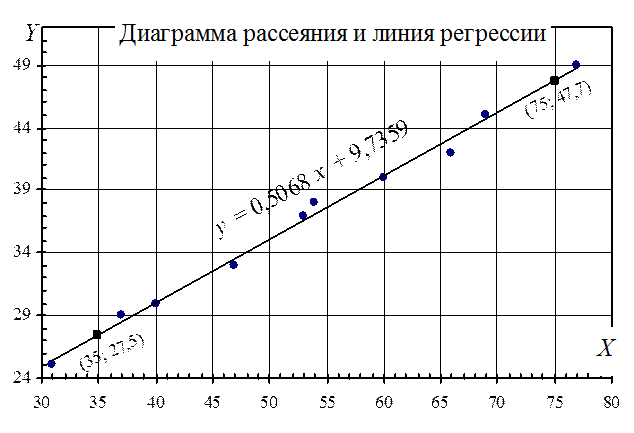
Построим диаграмму рассеяния. Для этого на плоскости ХOУ отметим точки с координатами (x_i ; y_i).

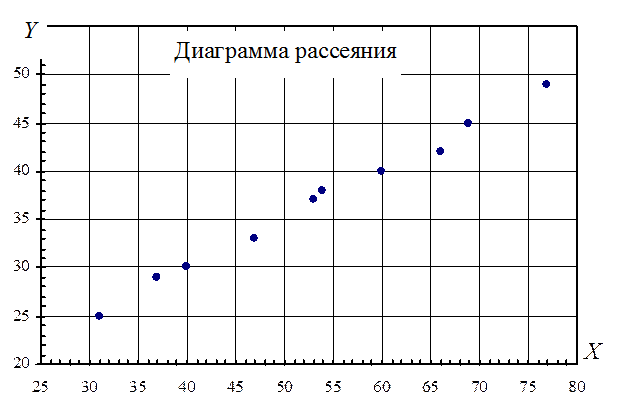
По диаграмме рассеяния видно, что точки (x_i ; y_i) группируются около некоторой прямой. Поэтому выборочное уравнение линейной регрессии будем искать в виде y = a∙x+b. Параметры a и b найдем методом наименьших квадратов. Составим систему нормальных уравнений:

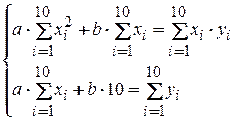
Вспомогательные вычисления проведем в следующей таблице:

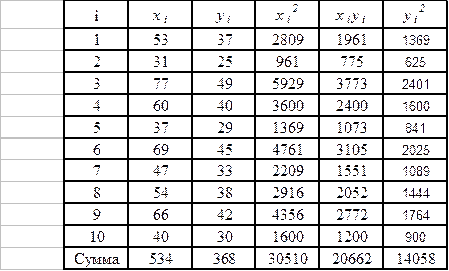
Итак, система нормальных уравнений имеет вид:

.

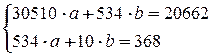Решим её с помощью определителей (методом Крамера). Определитель системы

.

.

.

, .

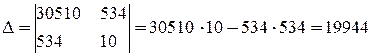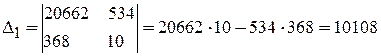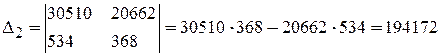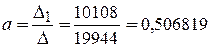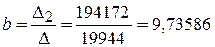Выборочное уравнение линейной регрессии имеет вид

y = 0,506819∙x+9,73586.

Чтобы построить линию регрессии найдем координаты двух точек, принадлежащих прямой y = 0,506819∙x+9,73586.

При x=35 y=0,506819∙35+9,73586=27,474529≈27,5.

При x=75 y=0,506819∙75+9,73586=47,747292≈47,7.

Линия регрессии – прямая, проходящая через точки (35; 27,5) и (75; 47,7).

Выборочный коэффициент линейной корреляции найдем по формуле

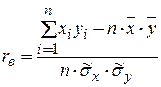, где 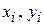– наблюдавшиеся значения признаков X и Y; 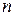– объём выборки; 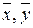– выборочные средние; 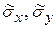– выборочные среднеквадратические отклонения.

. .

.

.

.

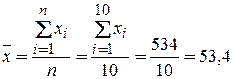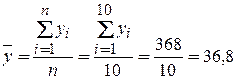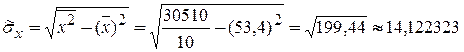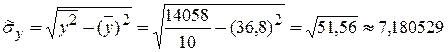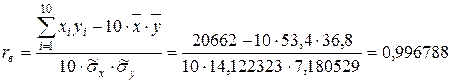Так как выборочный коэффициент линейной корреляции 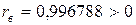, то корреляция положительная, т. е. с возрастанием x возрастает и y. Так как 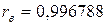очень близко к единице, то связь между признаками x и y тесная. Поэтому полученное уравнение регрессии y на x можно использовать для прогнозов. Оценим ожидаемое среднее значение y при X₀ = 55%.

y=0,506819∙55+9,73586=37,610911≈37,6

Ответ: уравнение регрессии y = 0,506819∙x+9,73586 можно использовать для прогнозов; связь между признаками x и y тесная, положительная. выборочный коэффициент линейной корреляции 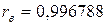. При концентрации растворенного вещества, равного 55 г средняя оптическая плотность раствора составляет 37,6.