Мода и медиана. Квантили. Моменты случайных величин. Асимметрия и эксцесс.

Кроме математического ожидания и дисперсии, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные свойства распределения.

Модой М_о(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность p_i или плотность вероятности φ(x) достигает максимума).

Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным (рис. 5.3)

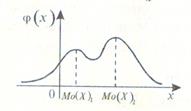
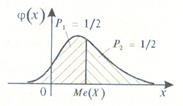
Рис. 5.3 Рис. 5.4

Медианой М_е(Х) непрерывной случайной величины Х называется такое ее значение, для которого

,

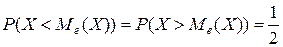т.е. вероятность того, что случайная величина Х примет значение, меньшее медианы М_е(Х) или большее ее, одна и та же и равна 1/2. Геометрически вертикальная прямая x=М_е(Х), проходящая через точку с абсциссой, равной М_е(Х), делит площадь фигуры под кривой функции распределения на две равные части (см. рис. 5.4). очевидно, что в точке x=М_е(Х) функция распределения равна 1/2, т.е. F(М_е(Х))= 1/2 (рис. 5.5).

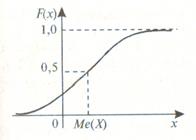
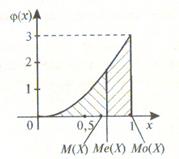
Рис. 5.5 Рис. 5.6

Пример 5.2.13. Найти моду, медиану и математическое ожидание случайной величины Х с плотностью вероятности 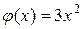при xÎ[0; 1].

○ Кривая распределения представлена на рис. 5.6. Очевидно, что плотность вероятности 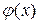максимальна при x=М_о(Х)=1.

Медиану М_е(Х)=b найдем из условия

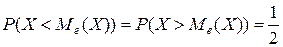, т.е. 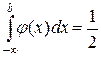или

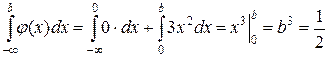, откуда

.

.

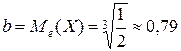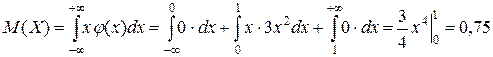Взаимное расположение точек М(Х), М_е(Х) и М_о(Х) в порядке возрастания абсцисс показано на рис. 5.6. ●

Квантилем уровня q (или q-квантилем) называется такое значение x_q случайной величины Х, при котором функция ее распределения принимает значение, равное q, т.е.

F(x_q)=P(X<x_q)=q.

Некоторые квантили получили особое название. Очевидно, что медиана случайной величины есть квантиль уровня 0,5, т.е. М_е(Х)=x_0,5. Квантили x_0,25 и x_0,75 получили название соответственно верхнего и нижнего квантилей[1].

С понятием квантиля тесно связано понятие процентной точки. Под 100%-ной точкой подразумевается квантиль x_1-q, т.е. такое значение случайной величины Х, при котором P(X³x_1-q)=q.

Пример 5.2.14. По данным примера 5.2.13. найти квантиль x_0,3 и 30%-ную точку случайной величины Х.

○

Найдем F(x):

.

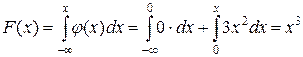Квантиль x_0,3 найдем из уравнения F(x_q)= q, т.е. 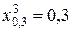, откуда .

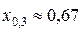Найдем 30%-ную точку случайной величины Х, или квантиль x_0,7, из уравнения 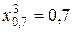, откуда .●

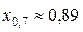Начальный и центральный моменты k-го порядка для непрерывной случайной величины определяются также как и для дискретной (см. 5.2.2.5).

Момент	Случайная величина
Дискретная	Непрерывная
Начальный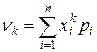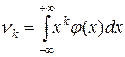
Центральный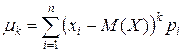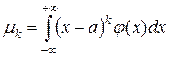

Отметим, что математическое ожидание М(Х), или первый начальный момент ν₁, характеризует среднее значение или положение распределения случайной величины Х на числовой оси; дисперсия D(X), или второй центральный момент m₂, – степень рассеяния распределения Х относительно М(Х). для более подробного описания распределения служат моменты высших порядков.

Третий центральный момент m₃ служит для характеристики асимметрии (скошенности) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на 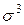, где 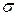– среднее квадратическое отклонение случайной величины Х. Полученная величина называется коэффициентом асимметрии случайной величины:

.

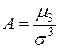Если распределение симметрично относительно математического ожидания, то коэффициент асимметрии А=0.

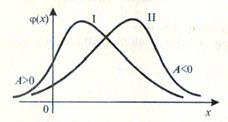
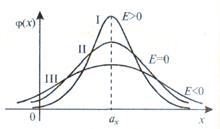
Рис. 5.7 Рис. 5.8

На рисунке 5.7 показаны две кривые распределения: I и II. Кривая I имеет положительную (правостороннюю) асимметрию (А>0), а кривая II – отрицательную (левостороннюю) (А<0).

Четвертый центральный момент m₄ служит для характеристики крутости (островершинности или плосковершинности) распределения.

Эксцессом (или коэффициентом эксцесса) случайной величины называется число

.

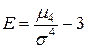Число 3 вычитается из отношения 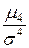потому, что для наиболее часто встречающегося нормального распределения (о нем речь пойдет в 5.2.4.5) отношение 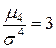. Кривые, более островершинные, чем нормальная, обладают положительным эксцессом, более плосковершинные – отрицательным эксцессом (рис. 5.8).

Пример 5.2.15.Найти коэффициент асимметрии и эксцесс случайной величины, распределенной оп так называемому закону Лапласа с плотностью вероятности .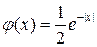

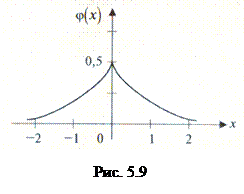
○Так как распределение случайной величины Х симметрично относительно оси ординат (рис. 5.9), то все нечетные как начальные, так и центральные моменты равны 0, т.е. ν₁=0, ν₃=0, m₃=0. Тогда коэффициент асимметрии .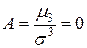

Для нахождения эксцесса необходимо вычислить четные начальные моменты ν₂ и ν₄:

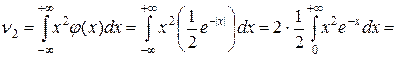
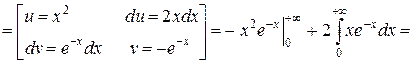
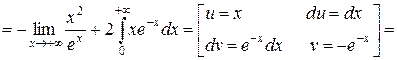
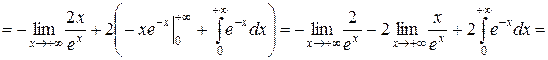
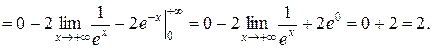
Следовательно,

D(X)=m₂= 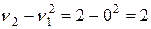и .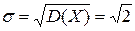

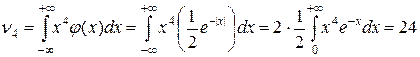, тогда

.

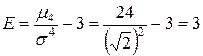Эксцесс распределения положителен, что говорит об островершинности кривой распределения 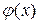(рис. 5.9).●