Применение поверхностных интегралов к решению краевых задач

Метод разделения переменных и метод функции источника (Грина) позволяют получать явное выражение для решения краевых задач только в случае областей простейшего вида. Сведение краевых задач для уравнения Лапласа или Пуассона при помощи поверхностных интегралов к интегральным уравнениям, с одной стороны, удобно для теоретического исследования вопроса существования и единственности решения краевых задач, а с другой стоны, создает возможность для эффективного численного решения краевых задач для областей сложной формы.

Сформулируем внутренние краевые задачи для некоторого контура С.

Найти функцию u, гармоническую в области Т, ограниченной контуром С, и удовлетворяющие на этом контуре граничным условиям:

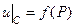для первой краевой задачи

или

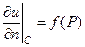для второй краевой задачи

Аналогично ставятся и внешние краевые задачи, причем при постановке второй краевой задачи как внутренней, так и внешней, в граничном условии нормаль будем считать внутренней.

Будем искать решение первой внутренней краевой задачи в виде потенциала двойного слоя

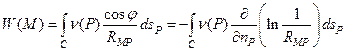, (24)

где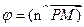

Как мы помним, функция W(M) разрывна на контуре С, поэтому для обеспечения непрерывности решения, в качестве граничного условия нужно взять W_в(Р₀), т.е.

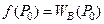
Тогда формулу (17) §6, можем записать в виде

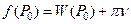
При этом W(P₀) имеет вид

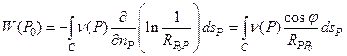
В результате окончательно можно записать

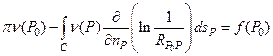(25)

Это есть не что иное как уравнение для нахождения ν(Р). Если обозначить через s₀ и s дуги контура С, отсчитываемые от некоторой начальной точки до точек Р₀ и Р, то это уравнение можно записать в следующем виде

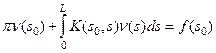(26)

где L – длина контура С.

Это уравнение является интегральным уравнением Фредгольма второго рода. Получив в результате решения интегрального уравнения функцию ν(s) или, что тоже самое, ν(Р), мы можем записать решение задачи в виде Функция переменных K(s₀, s) называется ядром этого уравнения и имеет вид

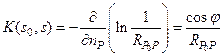(27)

Для внешней краевой задачи мы для обеспечения непрерывности решения мы должны во второй формуле (17) подставить граничное условие f(P₀) вместо W_в(Р₀). Тогда после перехода к переменной s получим

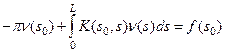(28)

При решении второй краевой задачи (по-прежнему для случая двух переменных) мы будем искать решение в виде потенциала простого слоя

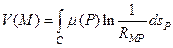(нормаль внутренняя) (29)

Функция V(M) непрерывна на контуре С, однако граничное условие второй краевой задачи содержит производную по нормали, которая для V(M) терпит в точке Р₀ разрыв, описываемый в случае внутренней нормали формулой

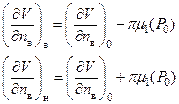(30)

Для обеспечения непрерывности решения внутри области, в качестве граничного условия нужно взять 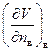, т.е.

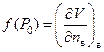
Теперь условие разрыва, описываемoе первой формулой в (28) можем переписать в виде

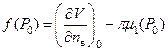
где функция 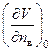имеет вид

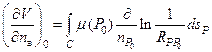
В результате окончательно можно записать

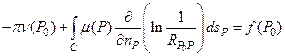(31)

Уравнение для нахождения μ(Р). Обозначая, как и раньше, через s₀ и s дуги контура С, отсчитываемые от некоторой начальной точки до точек Р₀ и Р, можем записать это уравнение в следующем виде

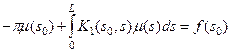(32)

Для внешней задачи получим аналогичное интегральное уравнение

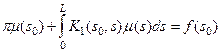(31)

где 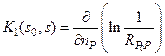– ядро интегрального уравнения Фредгольма второго рода. Это уравнение служит для определения плотности μ (s), знание которой позволит нам записать решение задачи в виде

Легко видеть, что ядро 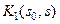можно получить из ядра K(s₀, s), поменяв местами переменные s₀ и s, т.е.

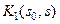= K(s, s₀)

Такие ядра называются взаимно сопряженными.

Задача Дирихле для круга

Если контур С является окружностью радиуса R, то внутренняя нормаль в точке Р направлена по диаметру, а значит

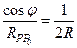, (32)

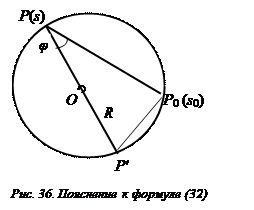так как φ – есть угол Р₀РР' (Рис. 36). Тогда интегральное уравнение для функции ν(s₀) принимает вид

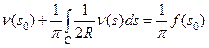(33)

Нетрудно убедиться, что его решением будет функция

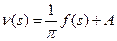(34)

где А – некоторая постоянная, которую мы определим, подставляя выражение для ν(s) (34) в интегральное уравнение (33)

,

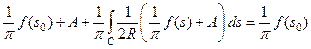откуда находим для постоянной А выражение через заданную функцию f (s)

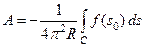
Таким образом, функция

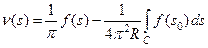(35)

является решением интегрального уравнения (33).

Соответствующий потенциал двойного слоя будет равен

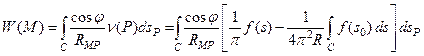
Преобразуем правую часть этой формулы, предполагая, что М лежит внутри С:

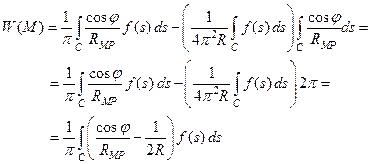(36)

Из Δ ОРМ (Рис. 37) видно, что

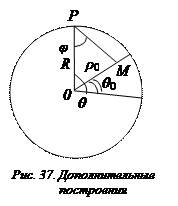
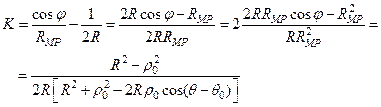, (37)

так как

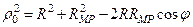
Подставляя теперь формулу (37) для К в формулу (36), мы получим уже знакомый нам интеграл Пуассона (§ 11, Гл. VI)

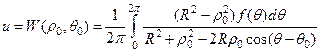, (38)

дающей решение задачи Дирихле для круга.

Замечание.Проведенные в этом параграфе рассуждения показывают, что при любой непрерывной функции f формула (37) определяет гармоническую функцию, непрерывно примыкающую к граничным значениям f.

Г л а в а.VIII. Уравнение Гельмгольца