Решение задачи Дирихле для уравнения Лапласа методом разделения переменных. Интегральная формула Пуассона.

Поставим для уравнения Лапласа внутреннюю задачу Дирихле для единичного круга. В этом случае выбираем полярную систему координат, в которой уравнение Лапласа имеет вид

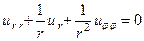(76)

с граничными условиями

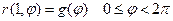(77)

Следует отметить, что сформулированная задача весьма актуальна с физической точки зрения. Помимо знакомых нам задач о распределении тепла при заданной температуре на границе области и распределении электростатического потенциала по заданному распределению его по границе можно привести также задачу о мыльной пленке. Если сделать кольцо так, чтобы отклонения от окружности в направлении ей перпендикулярному были малы и описывались функцией g (φ), то после погружения кольца в мыльный раствор, то мыльная пленка натянется на кольцо в соответствии с его формой. Возвышения точек пленки будут описываться решением поставленной выше задачей.

Границы применимости задачи, сформулированной для круга, расширяются с помощью конформных преобразований, при которых единичная окружность может быть преобразована в достаточно широкий набор кривых, интересных с практической точки зрения.

Поставленную выше задачу будем решать методом разделения переменных уже знакомым нам по решению уравнения колебаний и по решению уравнения теплопроводности. Как и раньше представим искомую функцию в виде произведения, а именно

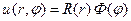
Если подставить это выражение в исходное уравнение (76), умножив обе части на r² и разделив на произведение 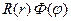, тополучим

,

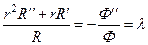где λ=const. Отсюда получаем два уравнения

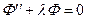(78)

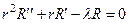(79)

Первое уравнение, как нам уже известно, имеет решение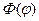

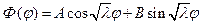
В силу периодичности функции Φ (φ) число 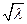может быть только целым числом n и тогда для каждого n будем иметь

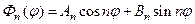(80)

Решение уравнения (79) ищем в виде 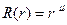. Подставив его в уравнение (79) и разделив все члены на r², мы получим

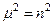или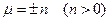

Следовательно,

(81)

Для решения внутренней задачи Дирихле надо отбросить второе слагаемое, так как, если D_n ≠0, то функция R_n (r), а вместе с ней и функция 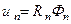обращается в бесконечность при 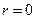, а значит и не является гармоничной внутри круга. Для решения внешней задачи Дирихле, наоборот, надо отбросить первое слагаемое (81), поскольку решение должно быть ограничено на бесконечности. Таким образом, частные решения нашей задачи можно записать следующим образом:

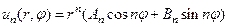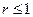
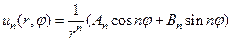для

для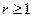

Суммы этих решений

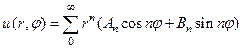для внутренней задачи и

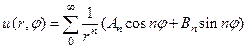для внешней задачи

при достаточно хорошей сходимости рядов также будут гармоническими функциями и представлять собой общее решение задачи Дирихле.

Для определения констант A _n и B_n подставим полученное решение в граничное условие

(82)

Поскольку функция 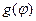периодическая, то мы можем разложить её в ряд Фурье

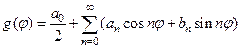, (83)

где ,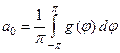

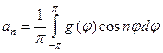(n =1, 2, . . .), (84)

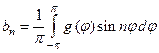(n =1, 2, . . .).

Сравнивая ряды (82) и (83) видим, что A _n = a _n и B_n = b_n .

Таким образом, мы получили решение внутренней и внешней задач Дирихле в единичном круге

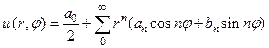для внутренней задачи и (85)

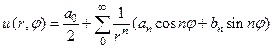для внешней задачи (86)

в которых коэффициенты a _n и b_n вычисляются по формулам (84).

З а м е ч а н и е. Нетрудно показать, что решение задачи Дирихле для круга произвольного радиуса а будет выглядеть следующим образом

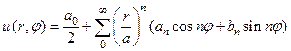для внутренней задачи и (87)

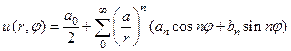для внешней задачи (88)