Уравнения Пуассона и Лапласа

К стационарным задачам математической физики относятся задачи о статическом распределении некоторой физической величины в заданной области. Большинство из них является частным, стационарным случаем задач, описываемых параболическими уравнениями. В том случае, когда эта величина обладает потенциалом, ставят задачу о распределении потенциала в заданной области. К стационарным задачам математической физики относятся

- задача о распределении электрического потенциала в некоторой области при заданном распределении в ней электрических зарядов,

- задача о распределении температуры в заданном объеме, обусловленной наличием в нем распределенных источников тепла,

- задача о распределении потенциала силы тяготения,

- задача о распределении поля скоростей в безвихревом потоке несжимаемой жидкости.

Во всех этих случаях задача сводится к уравнению Пуассона

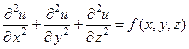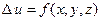или , (1)

где f (x, y, z) – c точностью до коэффициента удельная плотность источников. В отсутствии источников (тепла, электрических зарядов, жидкости) уравнение становится однородным и называется уравнением Лапласа.

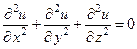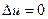или (2)

Для уравнений (1) и (2) должны быть сформулированы граничные условия, которые, как и для нестационарных задач, могут быть трех видов.

1) Первая краевая задача или задача Дирихле.

В этой задаче на границе замкнутой области S задается искомая функция (как функция точки):

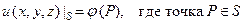(3)

В § 6будет доказана единственность решения этой задачи.

2) Вторая краевая задача или задача Неймана

В этой задаче на границе замкнутой области S задается производная по нормали от искомой функции:

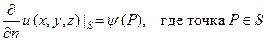(4)

У этой краевой задачи есть две особенности.

Во-первых, для обеспечения стационарности внутренней задачи необходимо, чтобы суммарный поток искомой функции u через границу области был равен нулю в отсутствии источников (уравнение Лапласа) или суммарной мощности источников при их наличии (уравнение Пуассона). Поскольку поток в каждой точке пропорционален нормальной производной функции u, то для уравнения Лапласа должно выполняться условие

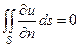, (5)

а для уравнения Пуассона

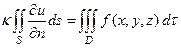, (6)

где 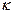– коэффициент пропорциональности при определении потока, а f – плотность источников. Эта особенность, как будет показано в § 5, непосредственно следует из первой формулы Грина, которая будет выведена в § 4

Во-вторых, задача Неймана имеет бесконечное множество решений отличающихся друг от друга на константу, в чем мы убедимся в § 6 (Лекция 14).

3) Третья краевая задача, которую иногда называют задачей Робена.

В этой задаче на границе замкнутой области S задается сумма искомой функции и её производной по нормали с некоторым постоянным коэффициентом:

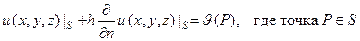(7)

В §6будет доказана единственность решения этой задачи.

Перечисленные выше краевые (граничные) условия называют внутренними или внешними в зависимости от того, ставятся ли они для области, лежащей внутри или вне конечной области, ограниченной замкнутой поверхностью. Если границей области является плоскость, то говорят, что ставится граничная задача для полуространства.

Как отмечалось во введении, задачу математической физики называют поставленной корректно, если её решение существует, единственно и непрерывно зависит от данных задачи.

Следует отметить, что условия, обеспечивающие корректность постановки той или иной граничной задачи, несколько различаются для разного типа задач. Однако существует группа условий, входящих во все эти формулировки. Она сводится к следующему.

Функция, являющаяся решением граничной задачи, должна:

1) быть непрерывной в области постановки задачи вплоть до границы области;

2) иметь непрерывные вторые производные и удовлетворять заданному уравнению внутри области;

3) удовлетворять заданному граничному условию;

4) если область трехмерна и бесконечна, то при перемещении к бесконечно удаленной точке вдоль любого луча, принадлежащего области, стремиться к нулю.

Решения граничных задач, поставленных в трехмерных областях, удовлетворяющие перечисленным условиям, называют регулярными решениями.

Теперь рассмотрим ьатематическую постановку некоторых из перечисленных выше физических задач.

Стационарное тепловое поле

Если в некоторой области пространства D,заполненной однородным изотропным веществом с возможным наличием стационарных источников тепла, тепловое состояние не меняется, то можно рассматривать задачу о стационарном распределении температуры в этой области. Это не исключает наличие потоков тепла (при наличии источников и соответствующих граничных условиях), но эти потоки должны быть стационарными и не приводить к изменениям распределения температуры по области с течением времени. В этом случае время из рассмотрения процесса можно исключить. В связи с этим уравнение, описывающее стационарное распределение температуры по области D, можно получить, приравняв в уравнении теплопроводности (§5, Гл. IV) производную по времени нулю.

В результате получим уравнение Пуассона в виде

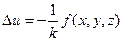(8)

где f (x, y, z) – удельная плотность источников тепла, k – коэффициент теплопроводности. Уравнение (8) не противоречит общему виду уравнения Пуассона (1), поскольку коэффициент 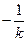может быть учтен в определении функции f (x, y, z).

В отсутствии источников тепла уравнение (3) становится уравнением Лапласа

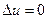(9)

Уравнения (8) и (9) должны быть дополнены соответствующими граничными условиями, вытекающими из конкретно поставленной задачи. В качестве таковых на границе обычно задается либо температура (первая краевая задача):

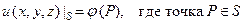, (10)

либо поток тепла, который с точностью до константы равен

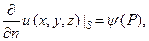(11)

т.е. вторая краевая задача,

либо температура окружающей среды на границе области, в которой решается задача. В этом случае, как мы видели (§ 2, гл. IV), мы приходим к третьей краевой задаче:

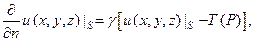(12)

где T(P) - температура окружающей среды на границе с областью или, что то же самое,

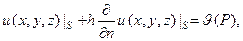(13)

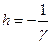где и .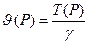

Уравнения электростатики.

Будем считать, что в некоторой среде-диэлектрике с диэлектрической постоянной e, электрическими зарядами, распределенными с плотностью r, образовано постоянное электрическое поле с напряженностью Е.

Если среда однородная, т.е. e = const, то по закону Кулона точечный заряд интенсивности е создаст потенциальное электрическое поле с напряженностью

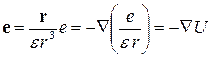, (14)

где r – вектор, соединяющий точку О, в которой находится заряд е, с переменной точкой пространства, U потенциал электрического поля (Рис. 26).

Поток вектора e e через поверхность сферы радиуса r с центром в точке О выразится следующим образом

Рис. 26. Поле точечного заряда

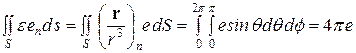(15)

Если теперь рассматривать заряд, распределенный по объему V с плотностью r, как совокупность точечных зарядов, то образованное таким образом поле также будет потенциальным, т.е. .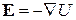

Поток вектора Ечерез замкнутую поверхность S будет равен

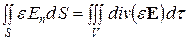(16)

С другой стороны

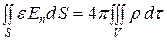(17)

Откуда следует, что при e =1

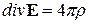, (18)

а поскольку 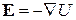, то

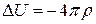(19)

Таким образом, для потенциала U мы имеем уравнение Пуассона, а в отсутствии зарядов – уравнение Лапласа

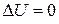(20)

Что же касается напряженности электрического поля, то для неё помимо уравнения (18) можно записать необходимое и достаточное условие того, что поле является потенциальным, а именно

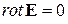(21)

Таким образом, уравнения (7) и (10) представляют собой систему уравнений в частных производных, называемую системой уравнений электростатики, к обсуждению которой мы вернемся позже. Что же касается задачи о распределении потенциала электрического поля в пространстве, описываемых уравнением Пуассона (19) или Лапласа (20), то в качестве граничного условия чаще всего ставится задача Дирихле, т.е. задается потенциал на границе области

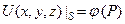(22)