Стратегия строго-периодического восстановления.

Согласно этой стратегии система восстанавливается после отказа. Если она проработала без отказов заданный интервал времени τ, то проводится профилактическая замена (рис.8.2). Восстановления, которые производятся после отказов, называются аварийными. Как профилактические, так и аварийные восстановления являются полными.

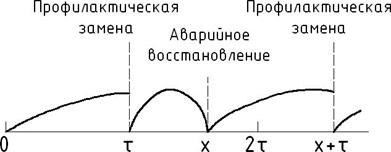
Рис.8.2 Строго периодическое восстановление

Согласно этой стратегии система восстанавливается после отказа. Если она проработала без отказов заданный интервал времени τ, то проводится профилактическая замена (рис.8.2). Восстановления, которые производятся после отказов, называются аварийными. Как профилактические, так и аварийные восстановления являются полными.

В дальнейшем предположим , что аварийное и профилактическое восстановления требуют .времени, равного соответственно d_h и d_p,( 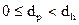.) В этом случае интервалы времени Y, на которых система восстанавливается, определяются соотношением

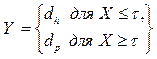
Отсюда следует

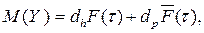
где F(t) – фнкция распределения времени безотказной работы; .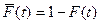

Таким образом коэффициент готовности системы K(τ) задается в виде

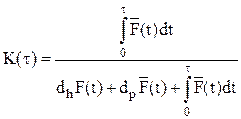
Задача состоит в максимизации коэффициента готовности К(τ) надлежащим выбором интервала восстановления τ.

Очевидно оптимальная периодичность будет удовлетворять условию оптимальности

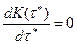
Из условия оптимальности следует

,

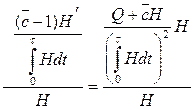где .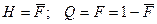

После преобразований имеем

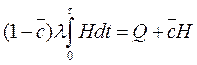
Отсюда

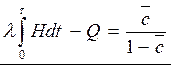
Пример выполнения задания №1.1

Результаты расчета представлены ниже ( см.рис.8.3)

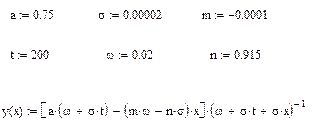
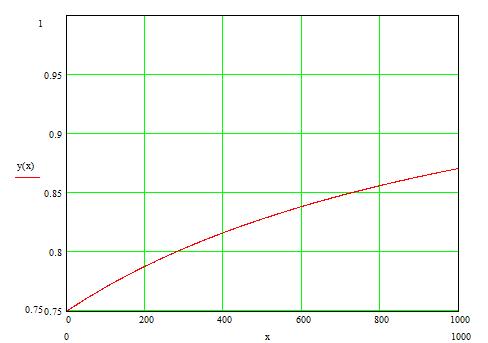
Рис. 8.3 Характер изменения упреждающего допуска y(x) 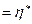от периодичности замен .

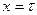При разработке программы были введены следующие обозначения:

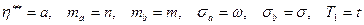
2. Построить график зависимости коэффициента готовности 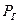в режиме хранения от периодичности обслуживания 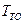и найти оптимальную периодичность замен 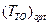при различных значениях времени обслуживания 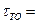5ч; 10ч; 30 суток; 100 суток и различных уровнях интенсивностей отказа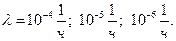

Основные расчетные соотношения

Граф состояний модели технического обслкуживания в режиме хранения представлен на рис. 8.4.

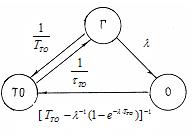
Рис. 8.4 Граф состояний системы.

В общем случае интенсивность перехода из состояния отказа (О) в состояние регламентного обслуживания (ТО ) будет равна

,

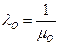где 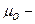среднее время нахождения системы в состоянии отказа.

Очевидно ,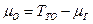

где 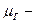среднее время нахождения системы в состоянии готовности в течении одного цикла.

С другой стороны 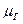можно рассматривать как математическое ожидание времени 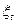между заменами произвольного типа

,

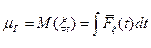где 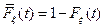, 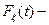функция распределения времени между заменами произвольного типа( см. рис. 8.5 ) .

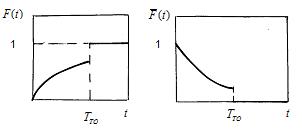
Рис. 8.5 Функция распределения 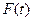и функция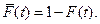

В рассматриваемом случае 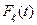будет равна

,

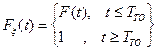где F(t) - функция распределения времени безотказной работы системы.

Для экспоненциального закона распределения получим

.

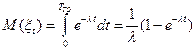Таким образом

.

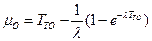Соответственно интенсивность перехода будет равна

.

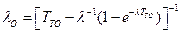Согласно графу вероятности нахождения системы в различных состояниях будут удовлетворять системе дифференциальных уравнений Колмогорова

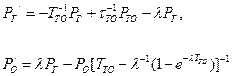
В стационарном режиме получим

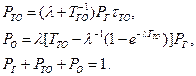
Разрешая систему относительно 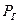, получим

.

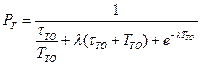В рассматриваемом случае периодичность РТО можно найти аналитически.

Очевидно оптимальные значения 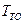должны удовлетворять условию

оптимальности

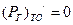, где .

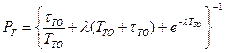Принимая 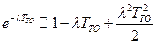, получим

.

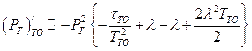Отсюда .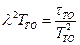

После преобразований окончательно получим .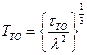

Пример выполнения задания №2.1

Расчеты коэффициента готовности проводились по соотношениям

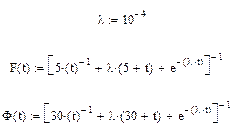
Результаты расчета коэффициента готовности представлены на рис.8.6

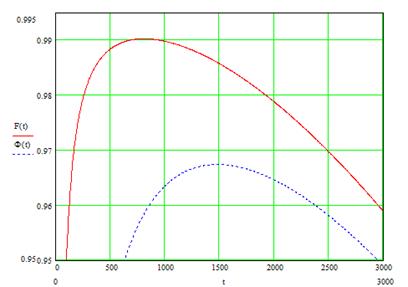
Рис. 8.6 Зависимость коэффициентов готовности F(t) пр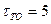и и

Ф(t) при 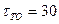от периодичности обслуживания .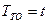