Оценка показателей надежности для закона распределения Вейбулла

В данном разделе предполагается, что наработка на отказ подчиняется распределению Вейбулла

.

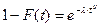Соответственно плотность распределения имеет вид

.

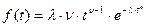Логарифм функции правдоподобия можно представить в виде

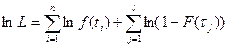
где 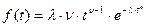- плотность распределения Вейбулла

Искомые параметры найдем из условий оптимальности

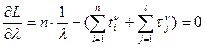
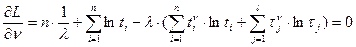
Разрешая уравнения относительно искомых параметров, найдем

;

.

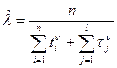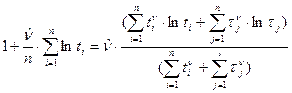Последнее уравнение решаются графическим методом.

Пример аыполнения задания №1

В результате испытаний получена выборка, содержащая 31 наработку до отказа ( полных реализаций) .

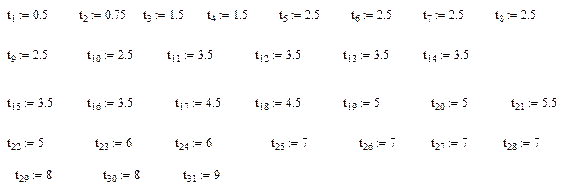
Расчеты проводились по соотношениям

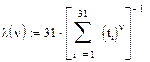
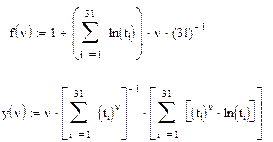
Уравнения решались графическим методом (см. рис.9.2 )

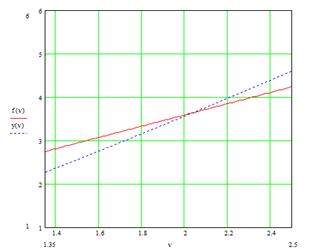
Рис.9. 2 Определение параметра формы .

Характер изменения 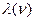представлен на рис.9.3.

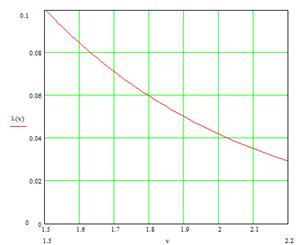
Рис.9.3. Изменение параметра масштаба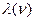

В данном случае имеем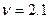

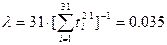
Оценка интенсивности отказа для различных планов проведения испытаний.

В данном разделе рассматриваются различные планы проведения испытаний для экспоненциального закона распределения времени до отказа

План [n,B,T] -- Испытания n элементов проводятся c заменой отказавших элементов

и прекращаются в момент T.

В рассматриваемом случае функция правдоподобия примет вид

,

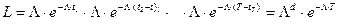где .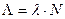

Условие оптимальности можно представить в виде

,

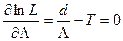где .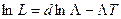

Отсюда .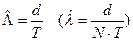

Полученная оценка является несмещенной, то-есть 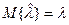. Действительно

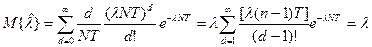
Кроме того оценка является состоятельной, то-есть .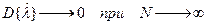

Для оценки дисперсии воспользуемся соотношением

,

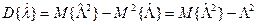где =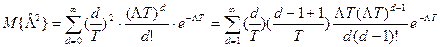

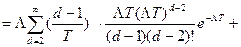
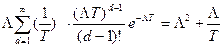
После подстановки получим

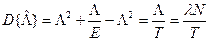
Соответственно для 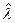будем иметь

.

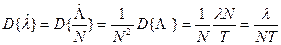Верхняя граница доверительного интервала 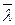удовлетворяет соотношению

.

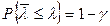Очевидно верхняя граница интенсивности отказа соответствует нижней границе надежности. Согласно определению односторонний доверительный интервал оценивается по соотношению

,

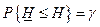где 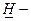нижняя граница одностороннего доверительного интервала.

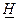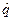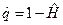Для нахождения рассматривается функция распределения статистики , где , которую можно представить в виде .

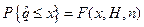Причем предполагается, что эта функция является непрерывной и возрастающей по H на отрезке [0,1]. Тогда 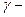нижней границей для H является корень уравнения

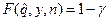(6.1)

Характер изменения функции 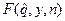по y представлен на рис.6. 4

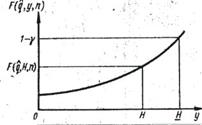
Рис.6.4 Характер изменения функции F (x, H, n) .

Отсюда видно, что при выполнении требований, предъявляемых к функции

F(x, y, n) , справедлива следующая цепочка утверждений

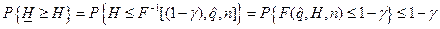
При переходе к последнему неравенству учитывалось, что если F(x)—функция распределения случайной величины 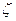, то выполняется соотношение

.

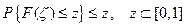Проиллюстрируем предложенный подход для оценки нижней границы надежности.

В рассматриваемом случае точечная оценка вероятности отказа будет равна 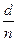. Отсюда

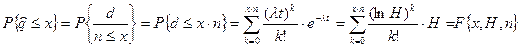
Согласно (2.1), нижняя граница надежности является корнем уравнения

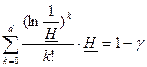или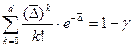

где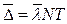

В дальнейшем представим равенство в виде

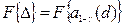
где 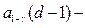квантиль распределения Пуассона.

Приравнивая аргументы, получим

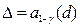
Отсюда окончательно найдем

.

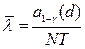Квантили распределения Пуассона представлены в табл. 9.1

Квантили распределения ПуассонаТаблица 9.1

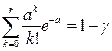
Значения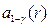

r / R/(1- 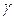)	0.5	0.4	0.3	0.2	0.1	0.05	0.025	0.01
	0.69	0.92	1.20	1.61	2.30	2.99	3.69	4.61
	1.68	2.02	2.44	2.99	3.89	4.74	5.57	6.64
	2.67	3.10	3.62	4.28	5.32	6.29	7.23	8.41
	3.67	4.17	4.76	5.51	6.68	7.54	8.77	10.04
	4.67	5.24	5.89	6.72	7.99	9.15	10.24	11.60
	5.67	6.29	7.00	7.91	9.27	10.51	11.67	13.11
	6.67	7.34	8.11	9.07	10.53	11.84	13.06	14.57
	7.67	8.39	9.21	10.23	11.77	13.15	14.42	16.00
	8.67	9.43	10.30	11.38	12.99	14.43	15.76	17.40
	9.67	10.48	11.39	12.52	14.21	15.71	17.08	18.78
	10.67	11.52	12.47	13.65	15.41	16.96	18.39	20.14
	11.67	12.55	13.55	14.78	16.59	18.21	19.68	21.49
	12.67	13.59	14.62	15.90	117.78	19.44	20.96	22.82
	13.67	14.62	15.70	17.01	18.96	20.67	22.23	24.14
	14.67	15.66	16.78	18.12	20.13	21.89	23.49	25.45
	15.67	16.69	17.83	19.23	21.29	23.10	24.74	26.74

План [n,В,r] -- Испытания n элементов проводятся с заменой отказавших элементов

и прекращаются после появления r отказов

В рассматриваемом случае функция правдоподобия примет вид

,

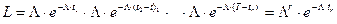где ,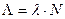

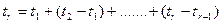
Условие оптимальности можно представить в виде

,

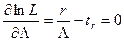где .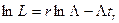

Отсюда .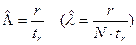

Случайная величина 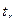, как сумма экспоненциально-распределенных случайных величин, подчиняется известному распределению

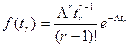
Отсюда

.

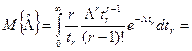
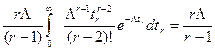Таким образом оценка , найденная выше, является смещенной. Для получения исключения смещения примем в качестве расчетной оценки соотношение

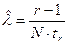
Верхняя граница доверительного интервала 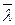оценивается по соотношению

.

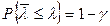Раскрывая выражение для вероятности, получим

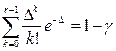
где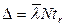

В дальнейшем представим равенство в виде

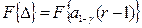
где 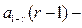квантиль распределения Пуассона.

Приравнивая аргументы, получим

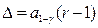
Отсюда окончательно найдем

.

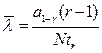План [n,Б,T] -- Испытания n элементов проводятся без замен отказавших элементов

и прекращаются в момент T.

В этом случае искомая оценка должна удовлетворять соотношению

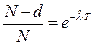
Отсюда

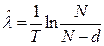
Одностороннй верхний доверительный интервал рассчитывается по соотношению

,

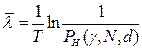где 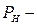односторонний нижний доверительный предел вероятности безотказной

работы при биномиальном законе распределения.

План [n,В,r] -- Испытания n элементов проводятся без замен отказавших элементов

и прекращаются после появления r отказов

По методу максимального правдоподобия приходим к смещенной оценке

,

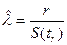где 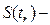сумма наработок всех испытываемых элементов.

Соответственно несмещенная оценка будет равна

.

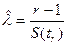Верхняя граница доверительного интервала оценивается по соотношению

.

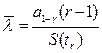Расчетные соотношения представлены в табл. 9.2

Сводка расчетных соотношений Таблица 9.2

Схема испытаний	NBT ( 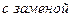)	NBr ( 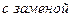)	NБТ ( 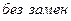)	NБr ( )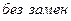
Точечная оценка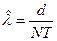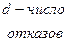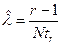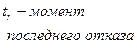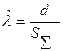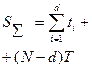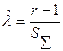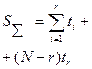
Интервальная оценка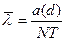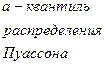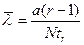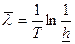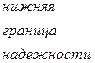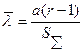

Пример №2

При проведении испытаний по плану [N,B,T] в течении Т=200ч. десяти изделий было зафиксировано десять отказов. Найти оценку 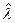и верхнюю границу доверительного интервала при .

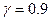Решние.

,

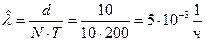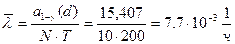
Пример 3.

При проведении испытаний по плану [N,B,r] двенадцати изделий, после наступления третьего отказа, который проявился в момент в момент 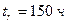, испытания были прекращены.. Найти оценку 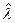и верхнюю границу доверительного интервала при .

,

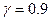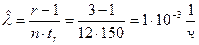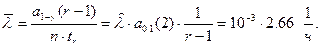
Пример 4

При проведении испытаний по плану [N,Б,T] в течении Т=100ч. пятидесяти изделий было зафиксировано пять отказов, а суммарная наработка равна 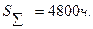Найти оценку 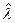и верхнюю границу доверительного интервала при .

,

( )

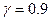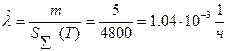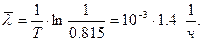
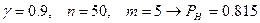Пример 5.

При проведении испытаний по плану [N,Б,r] двадцати изделий, после наступления третьего отказа испытания были прекращены. Отказы зафиксированы в следующие моменты: 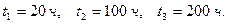Найти оценку 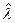и верхнюю границу доверительного интервала при .

,

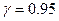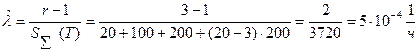Занятие №7