Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых известны (независимые выборки)

Пусть генеральные совокупности Х и Y распределены нормально, причем их дисперсии известны (например, из предыдущего опыта или найдены теоретически). По независимым выборкам, объемы которых соответственно равны n₁ и n₂, извлеченным из этих совокупностей, найдены выборочные средние 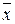и .

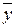Требуется по выборочным средним при уровне значимости a проверить нулевую гипотезу, состоящую в том, что генеральные средние (математические ожидания) рассматриваемых совокупностей равны между собой, т.е.

Н₀: М(X)=М(Y).

Проверка данной гипотезы дает ответ на вопрос: значимо или незначимо различаются выборочные средние. Если окажется, что нулевая гипотеза справедлива, т.е. генеральные средние одинаковы, то различие выборочных средних (в силу того, что последние являются несмещенными оценками генеральных средних, см. 6.1.4.) незначимо и объясняется случайными причинами и, в частности, случайным отбором объектов выборки.

Например, если физические величины А и В имеют одинаковые истинные размеры, а средние арифметические 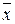и 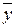результатов измерений этих величин различны, то это различие незначимое.

Если нулевая гипотеза отвергнута, т.е. генеральные средние неодинаковы, то различие выборочных средних значимо и не может быть объяснено случайными причинами, а объясняется тем, что сами генеральные средние (математические ожидания) различны.

Например, если среднее арифметические 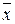результатов измерений физической величины А значимо отличается от среднего арифметического 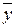результатов измерений физической величины В, то это означает, что истинные размеры (математические ожидания) этих величин различны.

Случай 1. Для того, чтобы при заданном уровне значимости a проверить нулевую гипотезу Н₀: М(X)=М(Y) о равенстве математических ожиданий двух нормальных генеральных совокупностей с известными дисперсиями при конкурирующей гипотезе Н₁: М(X)¹М(Y), надо

1. Вычислить наблюдаемое значение критерия:

.

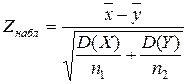2. По таблице значений функции Лапласа (приложение 2) найти критическую точку из равенства .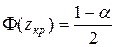

3. Если |Z_набл|<z_кр – нет оснований отвергнуть нулевую гипотезу.

Если |Z_набл|>z_кр – нулевую гипотезу отвергают.

Пример 6.2.5. По двум независимым выборкам, объемы которых соответственно равны n₁=60 и n₂=50, извлеченным из нормальных генеральных совокупностей Х и Y, найдены выборочные средние 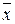=1250 и 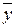=1275. Генеральные дисперсии известны: D(X)=120, D(Y)=100. При уровне значимости 0,01 проверить нулевую гипотезу Н₀: М(X)=М(Y) о равенстве математических ожиданий при конкурирующей гипотезе Н₁: М(X)¹М(Y).

○ Найдем наблюдаемое значение критерия:

.

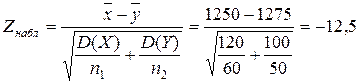По условию, конкурирующая гипотеза имеет вид Н₁: М(X)¹М(Y), поэтому критическая область – двусторонняя.

Найдем правую критическую точку из равенства:

.

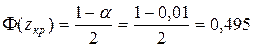По таблице значений функции Лапласа (приложение 2), находим z_кр=2,58.

Так как |Z_набл|>z_кр – нулевую гипотезу отвергаем. Другими словами, выборочные средние различаются значимо. ●

Случай 2. Для того, чтобы при заданном уровне значимости a проверить нулевую гипотезу Н₀: М(X)=М(Y) о равенстве математических ожиданий двух нормальных генеральных совокупностей с известными дисперсиями при конкурирующей гипотезе Н₁: М(X)>М(Y), надо

1. Вычислить наблюдаемое значение критерия:

.

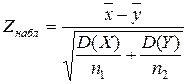2. По таблице значений функции Лапласа (приложение 2) найти критическую точку из равенства .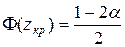

3. Если Z_набл<z_кр – нет оснований отвергнуть нулевую гипотезу.

Если Z_набл>z_кр – нулевую гипотезу отвергают.

Случай 3. Для того, чтобы при заданном уровне значимости a проверить нулевую гипотезу Н₀: М(X)=М(Y) о равенстве математических ожиданий двух нормальных генеральных совокупностей с известными дисперсиями при конкурирующей гипотезе Н₁: М(X)<М(Y), надо

1. Вычислить наблюдаемое значение критерия:

.

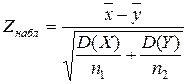2. По таблице значений функции Лапласа (приложение 2) найти критическую точку из равенства .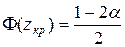

3. Если Z_набл>–z_кр – нет оснований отвергнуть нулевую гипотезу.

Если Z_набл<–z_кр – нулевую гипотезу отвергают.

Примечание.Если 1) генеральные совокупности распределены нормально, а дисперсии их неизвестны; 2) генеральные совокупности не распределены нормально и дисперсии их неизвестны, но при этом, в обоих случаях, выборки имеют большой объем (не менее 30 каждая) и независимы, то можно сравнивать средние так, как описано выше, заменив точный критерий Z_набл приближенным критерием:

,

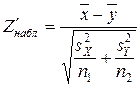где 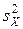, 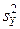– соответствующие выборочные дисперсии.

Однако, к выводам, полученным при помощи указанного приближенного критерия следует относиться осторожно.