Интервальные оценки основных числовых характеристик генеральной совокупности

Точечная оценка является лишь приближенным значением неизвестного параметра Θ и для выборки малого объема может существенно отличаться от Θ.

Чтобы получить представление о точности и надежности оценки 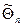параметра Θ, используют интервальную оценку параметров.

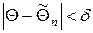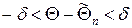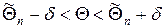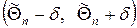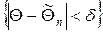Пусть d > 0 – некоторое число. Если выполняется неравенство , т.е. , что можно записать в виде , то говорят, что интервал накрывает параметр Θ. Однако невозможно указать оценку такую, чтобы событие было достоверным, поэтому говорят о вероятности этого события. Число d называют точностью оценки .

Определение 6.1.21. Надежностью (доверительной вероятностью или уровнем доверия) оценки параметра Θ для заданного d > 0 называется вероятность g того, что интервал 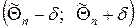покроет параметр Θ, т.е.

.

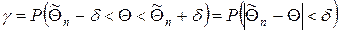Иными словами, g есть мера доверия вычисленной оценке .

Ясно, что чем меньше число d, тем меньше надежность g.

Определение 6.1.22. Доверительным интервалом называется найденный по данным выборки интервал 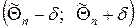, который накрывает параметр Θ с заданной надежностью g.

Надежность g обычно принимают равной 0,95 или 0,99, или 0,999.

Конечно, нельзя категорически утверждать, что найденный доверительный интервал накрывает параметр Θ. Но в этом можно быть уверенным на 95% при g=0,95, на 99% при g=0,99 и т.д. Это означает, что если произвести много выборок, то, например при g=0,95, для 95% из них вычисленные доверительные интервалы действительно накроют Θ.

Укажем доверительные интервалы для параметров нормального распределения а и s.

Утверждение 5.(Доверительный интервал для математического ожидания при известном s). С надежностью g можно утверждать, что доверительный интервал 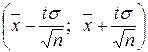накрывает неизвестный параметр а:

.

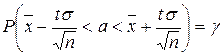Здесь точность оценки 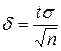, а число t определяется из равенства 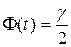по таблице приложения 2.

Пример 6.1.9. Признак Х распределен в генеральной совокупности нормально с известным s=0,40. Найти доверительный интервал для а с надежностью g=0,99, если n=20, .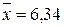

○Для 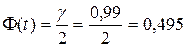находим по таблице приложения 2: t=2,58. Следовательно, 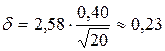. Тогда концы доверительного интервала равны 6,34–0,23=6,11 и 6,34+0,23=6,57. Итак, доверительный интервал (6,11; 6,57) накрывает а с надежностью 0,99. ●

Утверждение 6. (Доверительный интервал для математического ожидания при неизвестном s). С надежностью g можно утверждать, что доверительный интервал 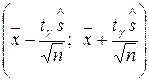накрывает неизвестный параметр а:

.

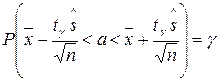Здесь точность оценки 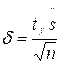, а число 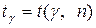определяется по таблице для 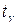приложения 4 для различных значений n и обычно задаваемых значений надежности g.

Пример 6.1.10. Признак Х распределен в генеральной совокупности нормально. Найти доверительный интервал для параметра а с надежностью g=0,99, если n=20, 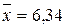, 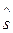=0,40.

○Для надежности g=0,99 и n=20 по таблице приложения 4 находим 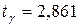. Следовательно, 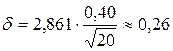. Тогда концы доверительного интервала равны 6,34–0,26=6,08 и 6,34+0,26=6,60. Итак, доверительный интервал (6,08; 6,60) накрывает а с надежностью 0,99. ●

Утверждение 7. (Доверительный интервал для среднего квадратического отклонения). С надежностью g можно утверждать, что доверительный интервал 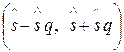накрывает неизвестный параметр s в случае q<1:

.

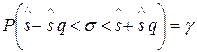В случае q>1:

.

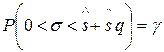Здесь точность оценки 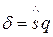, а число 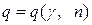определяется по таблице приложения 5 для различных значений n и обычно задаваемых значений надежности g.

Пример 6.1.11. Признак Х генеральной совокупности распределен нормально. Найти доверительный интервал для параметра s с надежностью g=0,95, если n=20, 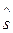=0,40.

○Для надежности g=0,95 и n=20 по таблице приложения 5 находим 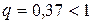. Следовательно, 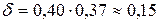. Тогда концы доверительного интервала равны 0,40–0,15=0,25 и 0,40+0,15=0,55. Итак, доверительный интервал (0,25; 0,55) накрывает s с надежностью 0,95. ●

Пример 6.1.12.Признак Х распределен в генеральной совокупности нормально. По выборке объема n=10 найдено «исправленное» среднее квадратическое отклонение 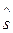=0,16 Найти доверительный интервал для параметра s с надежностью g=0,999.

○Для надежности g=0,999 и n=10 по таблице приложения 5 находим 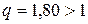. Следовательно, искомый доверительный интервал таков: 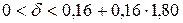или 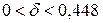. ●