Основы избыточного кодирования

Рассмотрим, для примера, полный набор трехразрядных кодовых слов Х₀-Х₇ (рис 6.1a).

Х0
Х1		Х0
Х2		Х3		Х0
Х3		Х5		Х7
Х4		Х6
Х5
Х6
Х7
	а)	б)			в)
Рис.6.1 Примеры кодов с разной избыточностью

Очевидно, что любая ошибка здесь приведет к неверному распознаванию переданного слова Х_i. Если ограничить набор допустимых кодовых комбинаций (например, по принципу четного количества «1» в слове), то одиночная ошибка при передаче приведет к приему недопустимого слова и ее можно будет обнаружить. Это достигается ценой избыточности (в примере для кодирования четырех символов достаточно было бы двух разрядов) – рис.6.1 б.

Наконец, если ограничиться лишь двумя словами, отличающимися в максимальном количестве разрядов, то обнаружить можно будет и двукратные ошибки, а однократные даже исправить (как видно по рис.6.1 в, слово искаженное однократной ошибкой, всегда "ближе" к своему прототипу, чем к другим словам кода). Разумеется, платой за это является дополнительная избыточность.

Обобщим эти замечания. Будем называть кодовым расстоянием d между двумя кодовыми словами количество несовпадающих разрядов (так для слов 100 и 010 d = 2, а для пары кодовых слов 010 и 011 значение d = 1). Полный набор кодовых слов характеризуется минимальным кодовым расстоянием d_min. Для безизбыточного кода (рис.6.1 а) d_min = 1, для кода, показанного на рис.6.1б d_min = 2, а для рис.6.1в - d_min = 3. Минимальное кодовое расстояние определяет гарантированную возможность обнаружения и исправления ошибок. Рис.6.2 наглядно иллюстрирует также следующие соотношения

- минимальная кратность r_m ошибок, которые могут быть распознаны

r_m = d_min-1 (6.1)

- максимальная кратность S_m ошибок, которые могут быть исправлены.

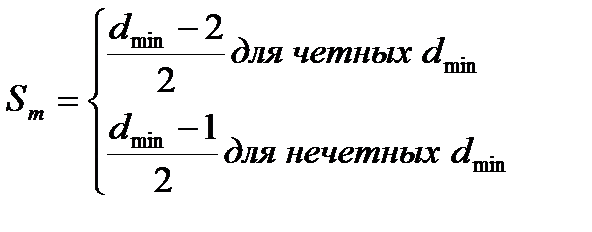(6.2)

- если ставится задача сочетать исправление ошибок кратности S < S_m и обнаружение ошибок более высокой кратности r, то

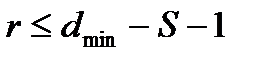(6.3)

Соотношения (6.1) – (6.3), как следует из определения d_min, рассчитаны на самый худший случай. В конкретных ситуациях иногда удается обнаружить и исправить ошибки и большей кратности.

Сделаем еще несколько общих замечаний относительно помехозащитных кодов

Во-первых, важной характеристикой кода является его способность противостоять так называемым «пачкам» ошибок (в соседних разрядах кодового слова). Под пачкой ошибок длиной l понимают набор соседних разрядов x_i – x_{i + l}, где разряды x_i и x_{i + l} ошибочны, а среди промежуточных x_j ( 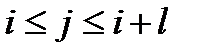) ошибки распределены произвольно. Существуют коды, которые распознают пачки ошибок длиной l >> d_min.

Во-вторых, чем больше длина кодовых слов, тем меньшую долю составляют избыточные разряды, обеспечивающие заданный уровень d_min. То есть, избыточное кодирование выгоднее выполнять именно для длинных слов.

В-третьих, избыточные разряды могут быть в принципе распределены по всей длине слова, однако чаще всего они образуют так называемый «хвостовик». В этом случае кодовое слово имеет следующую структуру:

x₁ … x_k x_k+1…x_k+m

Информационные разряды

Избыточные разряды

С практической точки зрения важна не только корректирующая способность кода, но также удобство и экономичность процедур, которые обеспечивают кодирование и декодирование. Особенности этих процедур во многом определяют области применения различных помехозащитных кодов. Ниже будут рассмотрены наиболее употребляемые из них.

Процедура кодирования подразумевает получение m избыточных разрядов х_j по k информационным (рис.6.3)

Процедура декодирования включает ряд проверок для полученных разрядов у_j , которые позволяют обнаружить и локализовать ошибки. В результате этих проверок формируется код, который принято называть опознавателем z (рис.6.3)

Систематические коды (CK) – это коды, у которых значения проверочных символов определяются в результате проведения линейных операций над определенными информационными символами.

Свойства систематических кодов:

1. В CK формирование проверочных элементов происходит по mинформационным элементам кодовой комбинации.

2. В CK проверочные символы (k) могут образовываться путем различных линейных комбинаций информационных символов.

3. Декодирование CK также основано на проверке линейных соотношений между символами, стоящими на определенных проверочных позициях.

4. Информационные (m) и корректирующие(k) символы в СК расположены по строго определенной системе и всегда занимают строго определенные места в кодовых комбинациях.

К систематическим кодам относятся коды Хэмминга, Голея, Рида-Маллера, Варшамова, Элайеса, Галагера, а также циклические коды.

Большинство систематических кодов отображаются при помощи производящей и проверочной матриц.

Определение. Порождающей (образующей, производящей) называется матрица, при помощи которой производится построение кода.

Определение. Проверочной называется матрица, при помощи которой строится система проверок при обнаружении и исправлении ошибок.

Код с проверкой на четность

Код с проверкой на четность

Этот код получил широкое распространение благодаря своей простоте. Пример такого кодирования был рассмотрен выше. В общем виде его можно описать так:

- кодирование сводится к операции 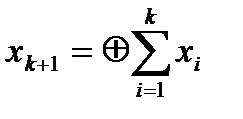(6.4), так, что контрольный бит с номером к+1 дополняет k информационных разрядов до четности;

- декодирование выполняется путем вычисления 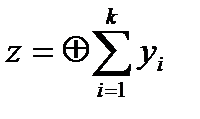(6.5), если Z=0 (четность соблюдена), считается, что передача произошла без ошибок, Z=1 свидетельствует об ошибке передачи.

Для такого кода d_min =2, а кратность гарантировано распознаваемых ошибок ч=1. Однако, его важное преимущество состоит в том, что он распознает все сочетания ошибок нечетной кратности (то есть, не только при r=1, но и r=3,5,7 и т.д. в зависимости от величины k).

Дополнительные возможности по обнаружению и корректировке ошибок дает так называемый код с проверкой на четность по строке и столбцу.

Поясним его особенности на примере рис.6.4

	x1	x2	x3	x4	x5
x1
x2
x3
x4
x0
a)

	y1	y2	y3	y4	y5
y1
y2
y3
y4
y0
б)
	y1	y2	y3	y4	y5
y1
y2
y3
y4
y0
в)

Пусть передаче подлежит блок из четырех четырехразрядных (k=4) кодовых слов х₁-х₄. Каждое слово дополняется проверочным разрядом х₅ по правилу четности. Кроме того дополнительно формируется проверочное кодовое слово X₀, все разряды которого получаются суммированием соответствующих бит передаваемых слов в блоке:

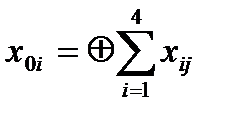
При однократной ошибке (рис.6.4б) проверка полученного блока кодовых слов Y_j показывает, что четность нарушена в четвертом ряде третьего слова. Указанные точкой координаты позволят исправить допущенную ошибку.

Минимальное кодовое расстояние такого кода равно произведению кодового расстояния по строке и столбцу: d_min=2х2=4, следовательно, максимальная кратность ошибок, обнаруживаемых кодом гарантировано r=4-1=3. Действительно, для r=4 существует ситуация, когда ошибки не обнаруживаются (соответствующий пример показан на рис.6.3). С другой стороны, в большинстве случаев даже при большом количестве ошибок в блоке их наличие будет установлено (убедитесь в этом самостоятельно, рассмотрев пример, подобно показанным на рис.6.4 б, 6.4 в.)

Отметим, что проверкой на четность по строке и столбцу (его называют также матричным кодом) применим лишь при передаче блоков кодовых слов.

Код Хэмминга

Циклические коды

Варианты заданий

1. Код с проверкой на четность (вычисление контрольного бита — по диагонали и горизонтали).

2. Код с проверкой на четность (вычисление контрольного бита — по вертикали и горизонтали).

3. Код Хэмминга (7,4)

4. Код Хемминга (15, 11)

5. Код Хемминга (31, 26)

6. Код Хемминга (63, 57)

7. Циклический код (7,4)

8. Циклический код (15,11).

9. Циклический код (21,11).

10. Циклический код (15,4).

11. Циклический код (15,7)

12. Код Хаффмана

13. Код Шеннона-Фано

14. Код с проверкой на четность (вычисление контрольного бита — по диагонали и горизонтали).

15. Код с проверкой на четность (вычисление контрольного бита — по вертикали и горизонтали).

16. Код Хэмминга (7,4)

17. Код Хемминга (15, 11)

18. Код Хемминга (31, 26)

19. Код Хемминга (63, 57)

20. Циклический код (7,4)

21. Циклический код (15,11).

22. Циклический код (21,11).

23. Циклический код (15,4).

24. Циклический код (15,7)

25. Код Хаффмана

26. Код Шеннона-Фано

27. (*) БЧХ-код

28. (*) Код Файра

29. (*) Код Голея

30. (*) Код Рида-Соломона

(*) – усложненные задания

Список литературы

1. Кодирование информации (двоичные коды). Б е р е з ю к Н. Т., Андрущенко А. Г., Мощнцкий С. С. и др. Харьков, из­дательское объединение «Вища школа», 1978. 252 с.

2. Золотарёв В. В., Овечкин Г. В. Помехоустойчивое кодирование. Методы и алгоритмы: Справочник / Под. ред. чл.-кор. РАН Ю. Б. Зубарева. - М.: Горячая линия-Телеком, 2004. - 126 с: ил.

3. Р. Морелос-Сарагоса Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. Москва: Техносфера, 2005. - 320с. I8ВN 5-94836-035-0

4. Бояринов И. М. Помехоустойчивое кодирование числовой ин­формации. – М.: Наука, 1983.

5.

6. Порядок защиты лабораторной работы

Лабораторная работа считается выполненной успешно при наличии у студента отлаженной программы, реализующей задание по варианту, а также отчета по лабораторной работе.

Программу и отчёт необходимо продемонстрировать преподавателю, ведущему лабораторные работы по дисциплине. Защита проделанной работы осуществляется в индивидуальном порядке.

7. Общие требования к оформлению отчёта по лабораторной работе

Отчёт по лабораторной работе выполняется на листах белой бумаги формата A4 в печатном или рукописном виде.

При оформлении отчёта используется сквозная нумерация страниц, считая титульный лист первой страницей. Номер страницы на титульном листе не ставится. Номера страницы ставятся по центру вверху или снизу.

Студенты имеют право оформлять отчёт как в рукописном варианте, так и использовать для оформления и печати ЭВМ и многофункциональные устройства.

При оформлении отчёта в печатном виде желательно соблюдать следующие требования. Для заголовков: полужирный шрифт, 14 пт, центрированный. Для основного текста: нежирный шрифт, 14 пт, выравнивание по ширине. Во всех случаях тип шрифта – Times New Roman, отступ абзаца 1 см, одиночный или полуторный междустрочный интервал. Поля: левое – 3 см, правое – 1 см, верхнее и нижнее – 2 см.

Отчёт формируется в следующем порядке:

Титульный лист.

Титульный лист оформляется в соответствии с образцом (см. стр. данного руководства).

Цель работы.

Цель работы показывает, для чего выполняется работа, например, для получения или закрепления каких навыков, изучения каких методов, алгоритмов и т.п.

Задание к лабораторной работе.

Задание к лабораторной работе включает две составляющие: общее задание (берется из теоретических сведений, указанных к каждой лабораторной работе) и задание по варианту. Варианты заданий размещены в описании к каждой лабораторной работе.