Раздел 1. Растяжение, сжатие

Растяжение и сжатие — такой вид нагружения, когда внешние силы действуют вдоль продольной оси бруса, при этом в его поперечных сечениях возникает только один внутренний силовой фактор — продольная сила. Прямой брус, работающий на растяжение (сжатие), называется стержнем. Применение метода сечений позволяет найти величину и направление внутренней продольной силы N, которая численно равна алгебраической сумме внешних осевых сил, действующих по одну сторону от рассматриваемого сечения. Если она направлена от сечения, т.е. является растягивающей, то считается положительной. В противном случае сжимающая сила считается отрицательной. Для наглядного изображения характера изменения продольной силы по оси стержня строят соответствующий график, который называется эпюрой.

При растяжении (сжатии) в поперечных сечениях стержня возникают только нормальные напряжения σ. На основании гипотезы плоских сечений все продольные волокна стержня испытывают одинаковые удлинения или укорочения. Следовательно, нормальные напряжения σ распределены равномерно по поперечному сечению стержня и определяются по формуле:

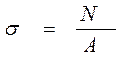, (1.1)

где N – внутренняя продольная сила, кН;

А – площадь поперечного сечения стержня, см².

Для обеспечения условия прочности элемента конструкции, в данном случае стержня, необходимо, чтобы наибольшее расчетное напряжение в его поперечном сечении было меньше того предельного напряжения, при котором возникает опасность разрушения или недопустимой эксплуатации конструкции. Количественно это условие имеет вид:

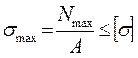, (1.2)

где [σ]- допускаемое нормальное напряжение, которое определяется экспериментально как предельное для данного материала с учетом коэффициента запаса прочности, зависящего от ответственности конструкции и условий ее эксплуатации, кН/см².

Из условия прочности (1.2) не представляет труда определить размеры поперечного сечения стержня, гарантирующие отсутствие разрушения:

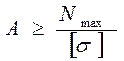, (1.3)

Как было указано выше, все продольные волокна стержня под действием внешних сил испытывают деформацию удлинения или укорочения. На основании закона Гука абсолютное удлинение (укорочение) стержня ∆l при действии продольной силы N вычисляется по формуле:

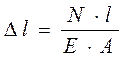, (1.4)

где, кроме прежних обозначений

l - длина стержня, см;

E - модуль продольной упругости (модуль Юнга), кН/см².

Для стержня со ступенчатым изменением площади А_i и нормальной силы N_i удлинение вычисляют на каждом участке с постоянными А_i и N_i, а результаты алгебраически суммируются:

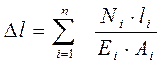, (1.5)

где n – число участков;

i – номер участка (i=1; 2; 3; …n)

Практическая работа №1

Для ступенчатого стального стержня, изображенного на рис. 1.1 построить эпюры продольных сил N и нормальных напряжений σ, а так же определить полную продольную деформацию стержня ∆l.

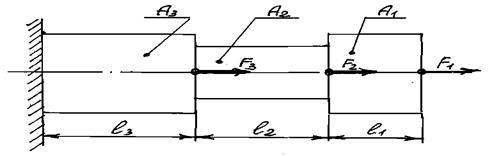
Рисунок 1.1 - Расчетная схема ступенчатого стержня

Таблица 1.1 – Исходные данные для выполнения практической работы № 1

Вариант	Исходные данные
F1, кН	F2, кН	F3, кН	А1, см2	А2, см2	А3, см2	l1, см	l2, см	l3, см
		-5	-8	1,8	2,3	1,4
	-20			1,2	1,9	1,7
			-16	2,4	1,6	2,1
		-10		1,5	2,6	1,9
	-8	-4		1,3	2,1	1,6
			-6	1,9	1,7	2,3
		-8		2,2	1,4	2,2
	-6	-4		0,8	2,2	0,8
			-20	1,4	0,8	1,8
	-9	-5		1,7	1,9	1,2
			-24	2,1	1,3	2,4
		-14		2,6	1,5	1,3
			-20	1,6	2,4	1,5
		-4		1,9	1,2	1,6
	-12			2,3	1,8	2,1
		-4	-7	1,9	2,4	1,5
	-19			1,3	2,0	1,8
			-15	2,5	1,7	2,2
		-9		1,6	2,7	2,0
	-7	-3		1,4	2,2	1,7
			-5	2,0	1,8	2,4
		-7		2,3	1,5	2,3
	-5	-3		0,9	2,3	0,9
			-19	1,5	0,9	1,9
	-8	-4		1,8	2,0	1,3
			-23	2,2	1,4	2,5
		-13		2,7	1,6	1,4
			-19	1,7	2,5	1,6
		-3		2,0	1,3	1,7
	-11			2,4	1,9	2,2

Модуль продольной упругости для стали Е= 2•10⁴ кН/см² (2•10⁵ МПа). Данные своего варианта взять из табл. 1.1.

Пример выполнения практической работы №1

Дано: F₁= 12 кН; F₂= -8 кН; F₃= 6 кН; А₁= 1,4 см²; А₂= 2,1 см²; А₃=1,8 см²; l₁ = 8 см; l₂ = 6 см; l₃ = 10 см; Е= 2•10⁴ кН/см²

Решение. Изображаем расчетную схему стержня в условном масштабе соответственно заданным в условии величинам площадей и длин участков. Направление внешних сил следует показывать в соответствии с заданным знаком, т.е. если сила задана положительная — растяжение, отрицательная — сжатие. Под изображенным стержнем оставляется место для эпюр N и σ, которые строятся после выполнения всех соответствующих вычислений. Эпюры строятся от осей абсцисс, которые проводятся параллельно продольной оси стержня, а значения N и σ откладываются по оси ординат вверх или вниз соответственно получившемуся знаку в условном масштабе. На эпюрах наносится тонкими вертикальными линиями штриховка, которая указывает направление ординат эпюры (рис. 1.2). Данное правило построения эпюр является общим и будет использоваться при выполнении последующих практических работ.

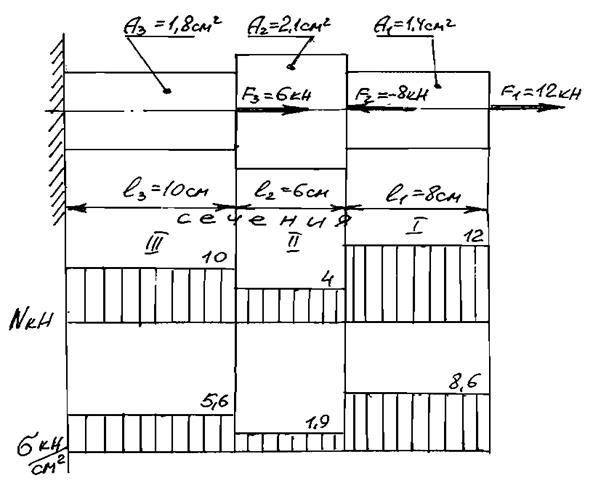
Рисунок 1.2 – Расчетная схема стержня и эпюры внутренних силовых факторов

1. Стержень разбивается на участки, границами которых являются сечения, соответствующие изменению площади поперечного сечения и приложению внешних сил. С учетом сказанного стержень разбивается на три участка.

2. Определение внутренней продольной силы N и последующее построение ее эпюры производим со стороны правого свободного конца (рис. 1.3).

Используя метод сечений на участке I имеем:

N=F₁=12 кН;

- на участке II:

N=F₁-F₂=12-8=4 кН;

- на участке III:

N=F₁-F₂+F₃=12-8+6=10 кН

Рисунок 1.3 – Расчетные участки стержня

Полученные значения продольных сил в пределах соответствующих участков стержня откладываем на графике, получая, соответственно, эпюру продольных сил.

3. Используя формулу (1.1), определяем значения нормальных напряжений σ в пределах соответствующих участков, где значение нормальной силы N снимается с эпюры.

Участок I

;

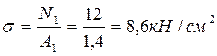Участок II

;

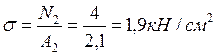Участок III

.

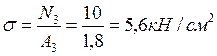Аналогично эпюре N строится эпюра нормальных напряжений σ. Эпюра нормальных напряжений показывает, что наибольшего значения нормальные напряжения достигают в пределах первого участка.

Знак "плюс" показывает, что в нашем случае в пределах каждого участка имеет место деформация растяжения, в случае знака "минус" — имела бы место деформация сжатия.

4. Определяем полную продольную деформацию стержня ∆l, которая алгебраически складывается из деформаций каждого из трех участков:

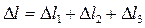
Используя формулу (1.4) вычисляем

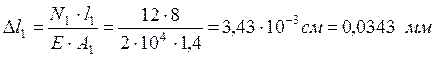
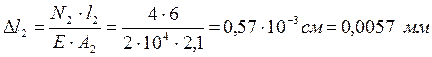
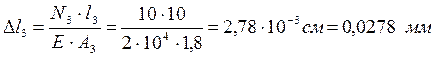
∆l = 0,343+0,057+0,278=0,0678 мм

Контрольные вопросы к разделу №1

1. Что называется растяжением (сжатием) бруса?

2. Чему равна величина внутренней продольной силы при растяжении (сжатии) бруса?

3. Что называется эпюрой и правила знаков при её построении?

4. Какие напряжения возникают в поперечных сечениях стержня и как они вычисляются?

5. Как записывается условие прочности для стержня?

6. Как определяется допускаемое напряжение материала стержня?

7. Как определяется абсолютное удлинение (укорочение) стержня?

Раздел 2. Сдвиг

Если в поперечных сечениях бруса возникает только поперечная сила, а остальные внутренние силовые факторы отсутствуют, то такой вид напряженного состояния называется сдвигом. В этом случае в сечении действуют только касательные напряжения, равнодействующей которых и является поперечная сила.

Сдвиг вызывает деформацию, представляющую собой искажение первоначально прямого угла элемента бруса под действием касательных напряжений. Развитие этой деформации приводит к разрушению, называемому срезом (применительно к древесине — скалыванием).

В предположении равномерного распределения касательных напряжений τ по сечению площадью А, они определяются по формуле:

, (2.1)

где Q – поперечная сила в данном сечении, кН.

На практике теория сдвига широко применяется к расчету болтовых, заклепочных, сварных и других элементов соединений.

2.1 Расчет болтовых и заклепочных соединений.

В зависимости от числа срезов одного болта или заклепки их называют односрезными (рис 2.1а), двухсрезными (рис. 2.1б) и т.д..

а) б)

Рисунок 2.1 – Схемы болтовых и заклепочных соединений

При значительной величине внешних сил F или небольшом диаметре заклепок, или при их недостаточном количестве они могут быть разрушены (срезаны) по сечению, расположенному в плоскости соприкосновения поверхности соединенных деталей. Условие прочности при расчете на срез болтовых и заклепочных соединений записывается в виде:

(2.2)

где, кроме прежних обозначений,

[τ] - допускаемое касательное напряжение на срез, которое определяется аналогично рассмотренному ранее [σ], кН/см².

Если соединение осуществлено несколькими одинаковыми заклепками или болтами, то считается что все они нагружены одинаково. Исходя из этого допущения условие прочности (2.2) записывается в виде:

(2.3)

где n - количество заклепок в соединении, шт.;

i – количество срезов на заклепке, равное числу соединенных деталей минус единица, шт.;

d - диаметр заклепок, см;

0,785•d² = - площадь поперечного сечения одной заклепки);

F - внешняя сила, действующая на соединение, кН.

Формула (2.3) позволяет, после соответствующих преобразований, выполнять любой вид расчета: определять наибольшую силу, которую выдержит заданное соединение, определять количество заклепок, их диаметр, обеспечивающих прочность соединения, или оценивать прочность соединения.

При небольшой толщине соединяемых деталей (листов) возникает большое взаимное давление по площади соприкосновения соединяемых деталей и заклепок, в результате чего стенка отверстия в детали или заклепке может получит пластическую деформацию смятия, при этом прочность заклепки на срез обеспечена.

Давление, возникающее между указанными поверхностями, действует по нормали к ним и называется напряжением смятия σ_cм. При практических расчетах на смятие, так же как и при расчетах на срез, считается, что все заклепки нагружены одинаково, а силы давления распределены по поверхности смятия равномерно. Отсюда условие прочности заклепочного (болтового) соединения на смятие имеет вид:

(2.4)

где d× δ – площадь смятия одной заклепки (или стенки отверстия детали) диаметром d при толщине детали δ .

[ σ_см ] – допускаемое напряжение смятия материала заклепки или детали. Если они изготовлены из разных материалов, то принимается наименьшая величина.

Допускаемое напряжение смятия является справочной величиной и в рамках данной практической работы приводится в качестве исходных данных.

При расчете количества заклепок на срез и смятие принимают большую величину, при этом расчет на смятие, как правило является проверочным.

2.2 Расчет сварных соединений.

Деформацию сдвига воспринимают сварные соединения, выполненные внахлест при помощи угловых швов, которые могут быть лобовыми (рис. 2.2а) и фланговыми (рис. 2.2б)

а) б)

Рисунок 2.2 – Схемы сварных соединений внахлест.

При расчете угловых швов (лобовых или фланговых) принимают, что опасное сечение шва, где может произойти разрушение, проходит через биссектрису АD прямоугольного треугольника ABC, за форму которого условно принимается поперечное сечение шва (рис. 2.3).

AB=AC=K

AD=0,7•K,

где К – катет углового шва.

Рисунок 2.3 – Схема поперечного сечения углового сварного шва

Таким образом, для углового шва площадь его поперечного сечения, по которому может произойти разрушение, определяется по формуле:

, (2.4)

где K, l - катет и длина шва соответственно, см.

Условие прочности сварных швов записывается аналогично условию прочности болтовых и заклепочных соединений:

, (2.5)

которое, также позволяет выполнять любой вид прочностных расчетов.

Практическая работа №2

Задача 2.1. Определить количество заклепок диаметром d, обеспечивающих прочность соединения листов, толщиной δ .

Проверить также прочность соединения на смятие и определить запас прочности по смятию. Заклепки изготовленs из стали с [τ ] (рис.2.4), а листы из стали с [σ_cv ]. Данные для задачи своего варианта взять из таблицы 2.1.

Схема I Схема II Схема III

Рисунок 2.4 – Расчетные схемы заклепочных соединений

Таблица 2.1 - Исходные данные для выполнения задачи 2.1 практической работы № 2

Исходные данные	Варианты
Схема	II	III	I	III	I	II	III	I	II	III
F, кН
[τ], кН/см2
d, мм
[σcv ], кН/см2
δ, мм	3,5	3,0	1,5	3,2	4,5	3,3	2,0	1,5	2,8	4,6

Продолжение таблицы 2.1

Исходные данные	Варианты
Схема	I	II	III	I	II	III	II	III	I	II
F, кН
[τ], кН/см2
d, мм
[σcv ], кН/см2
δ, мм	2,0	3,4	3,0	3,8	5,0	1,5	3,4	2,2	3,0	2,5
Исходные данные	Варианты
Схема	III	I	II	III	I	II	III	I	II	III
F, кН
[τ], кН/см2
d, мм
[σcv ], кН/см2
δ, мм	2,2	3,0	1,6	2,5	2,8	2,0	3,0	2,4	3,6	3,0

Задача 2.2. Определить наибольшую силу [F], которую выдержит сварное соединение (рис.2.5). Данные для задачи своего варианта взять из таблицы 2.2.

Схема I Схема II Схема III

Рисунок 2.5 – Расчетные схемы сварных соединений

Таблица 2.2 - Исходные данные для выполнения задачи 2.2 практической работы № 2

Исходные данные	Варианты
Схема	III	I	II	I	II	III	I	II	III	I
δ, мм
b, cм			-		-			-
l, cм		-		-			-			-
[τ], кН/см2

Продолжение таблицы 2.2

Исходные данные	Варианты
Схема	II	III	I	II	III	III	I	II	I	II
δ, мм
b, cм	-			-				-		-
l, cм			-				-		-
[τ], кН/см2
Исходные данные	Варианты
Схема	III	I	II	III	I	II	III	I	II	III
δ, мм
b, cм			-			-			-
l, cм		-			-			-
[τ], кН/см2

Пример выполнения задачи 2.1 практической работы №2.

Дано: Схема I; F = 95 кН; [τ]=16 кН/см² ; d =12 мм; [σ_см]= 52 кН/см² ; δ = 8 мм

Решение. Из условия прочности заклепок на срез (2.3) определяем их минимальное количество и полученный результат округляем до ближайшего большего целого числа.

Определяем количество срезов на заклепке для схемы своего варианта

i = 3 –1 = 2

Диаметр заклепки в «мм» переводим в «см» и производим необходимые вычисления

Принимаем в соединении 3 заклепки.

Выполняем проверку прочности соединения на смятие, используя выражение (2.4).

Толщину листа выражаем в «см» и производим необходимые вычисления

Прочность соединения на смятие обеспечивается со следующим запасом прочности

Пример выполнения задачи 2.2 практической работы №2

Дано: Схема II; δ = 3 мм; l = 12см; [τ ] = 18 кН/см²

Решение. Из условия прочности сварных швов (2.5) выражаем наибольшую силу [F], которую выдерживает данное сварное соединение.

Катет сварного шва «k» принимается равным толщине листов в сварном соединении и выражается в «см»

k = 3мм = 0,3 см

Определяем общую длину сварных швов, которая для данного варианта равна двойной длине флангового шва. Производим необходимые вычисления.

Наибольшая сила, которую выдержит сварное соединение

[F] = 90 кH

Контрольные вопросы к разделу №2

1. Что называется сдвигом?

2. Что называется срезом, скалыванием?

3. Какие соединения работают на сдвиг?

4. Какие допущения принимаются при практических расчетах болтовых и заклепочных соединений?

5. Какие заклепки называются одно- и многосрезными?

6. Как определяется площадь сечения углового сварного шва?