Частотный критерий устойчивости найквиста
Критерий Найквиста относится к частотным критериям устойчивости. Частотные методы исследования устойчивости основаны на связи расположения корней характеристического полинома (обозначим его функцией D(р) для любого типа систем) с годографом этого полинома на комплексной плоскости, т.е. с графиком комплексной функции D(jw) при изменении w от 0 до ∞. Это графоаналитические методы, позволяющие по виду частотных характеристик систем судить об их устойчивости. Их достоинство - в простой геометрической интерпретации, наглядности и в отсутствии ограничений на порядок дифференциального уравнения. В основу всех частотных критериев устойчивости положен принцип аргумента, основанный на правиле: изменение аргумента вектора D при изменении частоты от -∞ до +∞ равно разности между числом левых и правых корней уравнения D(p) = 0, умноженному на p, а при изменении частоты от 0 до +∞ эта разность умножается на p/2.
Так как для устойчивой системы число правых корней m = 0, то угол поворота вектора D(jw) составит
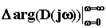 = np/2. (4.2.2)
= np/2. (4.2.2)
Критерий Найквиста основан на связи свойства устойчивости замкнутой системы с формой АФЧХ разомкнутой устойчивой системы. Разомкнутой системой являются все последовательно соединенные блоки от входа системы до точки замыкания обратной связи Исследование разомкнутой системы проще, чем замкнутой, и его можно производить экспериментально.
Передаточная функция Wpc разомкнутой системы:
Wpс(jw) = Kpc(jw)/Hpc(jw),
с углом поворота фазы в соответствии с выражением (4.2.2):
D arg Hрс(jw) = np/2, 0 ≤ w ≤ ∞. (4.2.3)
АФЧХ замкнутой системы описывается выражением:
Wзс(jw)= Wpc(jw) /[1+ Wpc(jw)]. (4.2.4)
Обозначим знаменатель этого выражения через W1(jw):
W1(jw)=1+Wpc(jw)=1+Kpc(jw)/Hpc(jw)=H(jw)/Hpc(jw), (4.2.5)
где H(jw) = Kpc(jw) + Hpc(jw), характеристический полином замкнутой системы при р=jw.
В соответствии со свойствами передаточных функций порядок полинома Н(р) не превышает порядка полинома Hpc(p), т.к. H(p)=Kpc(p)+Hpc(p), а порядок полинома Kpc(p) меньше порядка полинома Hpc(p). Поэтому критерий Михайлова для замкнутой системы соответствует выражению:
D arg H(jw) = (n - 2m) (p/2), 0 ≤ w ≤ ∞. (4.2.6)
где m - число правых корней системы, имеющей в замкнутом состоянии характеристический полином Н(р)=0.
Из (4.2.5) следует: D arg W1(jw) = D arg H(jw) - D arg Hpc(jw).
C учетом (4.2.3):D arg W1(jw) = (n - 2m) (p/2) - np/2 = -mp. (4.2.7)
В устойчивой замкнутой системе правых корней в характеристическом уравнении нет, т. е. m=0, а, следовательно, условием устойчивости замкнутой системы будет:
D arg W1(jw) = 0. (4.2.8)
Условие (4.2.8) выполняется только тогда, когда кривая W1(jw) при изменении частоты от 0 до ∞ не охватывает начала координат комплексной плоскости. Действительно, только в этом случае результирующий поворот вектора W1(jw) при изменении w от 0 до ∞ будет равен нулю, так как возрастание угла j(w), обусловленное движением вектора W1(jw) в положительном направлении (против часовой стрелки), будет компенсироваться таким же убыванием j(w), обусловленным движением вектора W1(jw) в отрицательном направлении (по часовой стрелке).
Как видно из (4.2.5),???? переход на комплексной плоскости от годографа вектора W1(jw) к годографу вектора АФЧХ разомкнутой системы Wpс(jw) осуществляется сдвигом кривой W1(jw) влево на -1, так как Wpc(jw) = W1(jw) -1. С учетом этой операции, получаем следующую формулировку амплитудно-фазового критерия устойчивости Найквиста: линейная динамическая система, устойчивая в разомкнутом состоянии, устойчива и в замкнутом состоянии, если АФЧХ разомкнутой системы Wpс(jw) при изменении частоты от 0 до ∞ не охватывает на комплексной плоскости точку с координатами (-1; j0) (рис. 4.2.4, годограф 2).
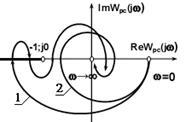 Рис. 4.2.4. Рис. 4.2.4. |
Более общая формулировка критерия Найквиста относится к системам, имеющим так называемую АФЧХ второго рода (рис. 4.2.4, годограф 1), когда Wpс(jw) пересекает (неограниченное количество раз) вещественную ось левее точки Re Wpc(w) = -1. Будем считать положительным переход годографа через вещественную ось, если он совершается сверху вниз, и отрицательным, если он совершается снизу вверх. Для таких годографов критерий Найквиста формулируется в следующем виде: линейная динамическая система, устойчивая в разомкнутом состоянии, устойчива и в замкнутом состоянии, если при изменении частоты от 0 до +∞ разность между числом положительных переходов годографа АФЧХ разомкнутой системы через участок вещественной оси (-1; -∞) и числом отрицательных переходов равна нулю.
Из этого условия видно, что система, устойчивая в разомкнутом состоянии и имеющая АФЧХ в форме кривой 1 на рис. 4.2.4, устойчива и в замкнутом состоянии.
Критерий Найквиста нагляден. Он позволяет не только выявить, устойчива ли система, но и, в случае, если она неустойчива, наметить меры по достижению устойчивости.
ОЦЕНКА УСТОЙЧИВОСТИ ПО ЛЧХ
Построение амплитудно-фазовых частотных характеристик разомкнутых систем связано с громоздкими вычислениями, поэтому целесообразно оценивать их устойчивость по логарифмическим частотным характеристикам. Для этого необходимо построить ЛЧХ разомкнутой системы (рис.5.14). На рис.5.14 условно показано четыре варианта возможного прохождения ЛФХ.
В том случае, когда АФЧХ не имеет точек пересечения с вещественной осью слева от точки с координатами (-1, j0), то для устойчивости замкнутой системы необходимо и достаточно, чтобы выполнялось условие ωс<ωкр.
То есть замкнутая система будет абсолютно устойчивой, если ЛАХ разомкнутой системы принимает отрицательные значения раньше, чем ЛФХ достигнет значения фазы -1800 (кривая 4 на рис.5.14).
Если ЛАХ разомкнутой системы принимает отрицательные значения позже, чем ЛФХ достигнет значения фазы -1800 (кривая 1 на рис.5.14), то замкнутая система неустойчивая.
Если ЛАХ разомкнутой системы принимает значение амплитуды 0 дб на одной частоте, что и ЛФХ достигнет значения фазы -1800 (кривая 2 на рис.5.14), то это соответствует колебательной границе устойчивости.
В условно устойчивых системах (кривая 3 на рис.5.14) для оценки устойчивости следует в диапазоне частот, где ЛАХ больше нуля, подсчитать число переходов ЛФХ через прямую -1800. Если число положительных (сверху вниз) переходов через эту прямую равняется числу отрицательных (снизу вверх), то система в замкнутом состоянии устойчива.
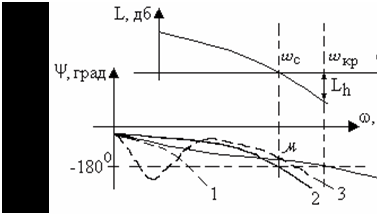
Рис. 5.14.
По ЛЧХ разомкнутой системы можно определить запасы устойчивости: запас по фазе μ отсчитывается по ЛФХ на частоте среза ωс, а запас по амплитуде Lh соответствует значению ЛАХ на критической частоте ωкр, взятому с обратным знаком (кривая 4 на рис.5.14).
Если ωс=ωкр, то система находится на границе устойчивости. Граничное значение общего коэффициента передачи разомкнутой системы kгр определяется из выражения:
20 lg kгр = 20 lg k + Lh,
где k - общий коэффициент передачи разомкнутой системы.
В заключение дадим некоторые рекомендации, которые следуют из практики проектирования систем.
Во-первых, для того чтобы в системе были обеспечены необходимые запасы устойчивости, наклон ЛАХ в диапазоне частот, в котором расположена частота среза, должен быть равным -20дб/дек. При наклоне характеристики, равном -40дб/дек, трудно обеспечить необходимый запас устойчивости по фазе. При наклоне характеристики, равном 0 дб/дек, получают излишне большие запасы устойчивости по фазе, система становится передемпфированной с длительным переходным процессом.
Во-вторых, запас устойчивости по фазе в системе зависит от диапазона частот, в котором ЛАХ разомкнутой системы на частоте среза имеет наклон -20дб/дек. Чем больше этот диапазон частот, тем выше запас устойчивости по фазе и наоборот.
ЛЕКЦИЯ № 11
АНАЛИЗ КАЧЕСТВА САУ
Устойчивость САУ является необходимым, но не достаточным условием эффективного функционирования системы. Не менее важно, чтобы процесс регулирования осуществлялся при обеспечении определенных показателей качества.
Понятие качества системы автоматического управления [33] включает требования по точности, характеру переходных процессов, виду задающих и внешних возмущающих воздействий и т.д.
В теории управления обычно рассматриваются, в основном, характеристики системы управления, связанные с ее динамикой и точностью. Указанные характеристики являются качественными, но в процессе проектирования систем часто возникает необходимость проводить сравнение различных вариантов. Поэтому вводятся специальные количественные эквиваленты качественных характеристик САУ. Эти численные характеристики называются показателями качества САУ. Они делятся на показатели качества в переходном режиме и показатели качества в установившемся режиме.
Динамические показатели качества служат для анализа динамики в системы переходном режиме, т.е. для анализа характера движений этой системы при переходе из одного установившегося состояния в другое. При этом необходимо, чтобы затухание переходного процесса было достаточно быстрым, а отклонения при этом были бы невелики.
Показатели качества в установившемся режиме характеризуют точность системы, т.е. качество поддержания ею требуемых законов изменения переменных управляемого процесса, чтобы это установившееся состояние было достаточно близко к заданному
Совокупность показателей качества переходного процесса и установившихся режимов называется показателями качества системы в целом.
ПОКАЗАТЕЛИ КАЧЕСТВА САУ
Для определения качественных показателей системы управления используются так называемые критерии качества.
Качество переходного процесса, которое оценивают по характеристикам переходной функции h(t), представляющей собой реакцию системы на внешнее воздействие типа единичной ступенчатой функции 1(t) рис. 5.2.
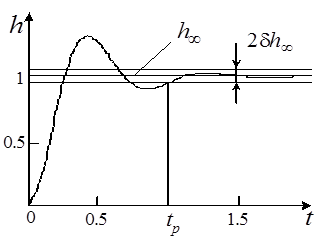
Рис. 5.2
Основными из этих показателей являются:
1. Установившееся значение переходной функции
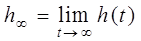 . (5.1)
. (5.1)
2. Время регулирования (время переходного процесса)
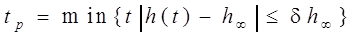 , (5.2)
, (5.2)
т.е. tp – это минимальное значение времени, при котором выполняется указанное в фигурных скобках условие. Учитывая, что полное затухание в системе происходит лишь при t→∞, длительность переходного процесса обычно ограничивают тем моментом времени, когда δ становится равным 0,05 h∞.
Фактически tp - это интервал времени от момента приложения на вход системы единичного скачка до момента после которого отклонение выходной величины от установившегося значения по модулю не превысит допустимую ошибку – δ, т.е. до момента, начиная с которого переходная функция системы 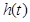 не выходит из “трубки”
не выходит из “трубки” 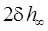 (рис. 5.2). Время регулирования tp определяет длительность переходного процесса и характеризует быстроту затухания переходного процесса. Этот показатель позволяет оценить быстродействие системы – важнейшую динамическую характеристику САУ.
(рис. 5.2). Время регулирования tp определяет длительность переходного процесса и характеризует быстроту затухания переходного процесса. Этот показатель позволяет оценить быстродействие системы – важнейшую динамическую характеристику САУ.
3. Перерегулирование. Перерегулирование Δhmax или выброс представляет собой максимальное отклонение регулируемой величины от установившегося значения. Обычно, первый максимум является наибольшим. Эта величина выражается в процентах и определяется по формуле
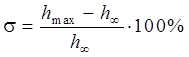 , (5.3)
, (5.3)
где 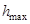 – максимальное значение переходной функции
– максимальное значение переходной функции 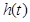 (см. рис. 5.2).
(см. рис. 5.2).
Перерегулирование появляется вследствие того, что система к установившемуся состоянию подходит с определенной скоростью. Чем больше эта скорость (круче кривая переходной функции), тем больше будет перерегулирование. Для уменьшения перерегулирования необходимо снизить скорость, с которой система подходит к установившемуся состоянию, что приведет к увеличению времени регулирования tp. Если система подходит к установившемуся состоянию с нулевой скоростью, то перерегулирования не происходит, но время регулирования значительно возрастает. Время регулирования и перерегулирование тесно связаны между собой обратной зависимостью. Таким образом, можно сделать вывод, что, как отсутствие, так и очень большое перерегулирование являются нежелательными. Поэтому перерегулирование допускают в пределах 10-30% от установившегося значения. Перерегулирование указывает на степень склонности системы к колебаниям, то есть близость системы к колебательной границе устойчивости.
В конечном итоге перерегулирование характеризует запасы устойчивости.
С увеличением перерегулирования запасы устойчивости уменьшается.
Перерегулирование характеризует качество переходных процессов системы.
4. Число колебаний 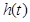 за время переходного процесса
за время переходного процесса
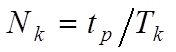 , (5.4)
, (5.4)
где 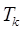 – период колебаний;
– период колебаний; 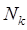 – число полных колебаний
– число полных колебаний 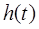 за время
за время 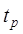 . Этот показатель вместе с перерегулированием характеризует колебательность системы.
. Этот показатель вместе с перерегулированием характеризует колебательность системы.
У нормально работающих систем составляет обычно 1÷3.колебания.
Показатели 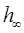 ,
, 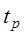 ,
, 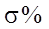 и
и 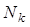 являются основными показателями качества переходного процесса САУ. Часто они называются прямыми показателями качества. Чем меньше
являются основными показателями качества переходного процесса САУ. Часто они называются прямыми показателями качества. Чем меньше 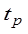 ,
, 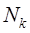 и
и 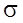 , тем выше качество системы.
, тем выше качество системы.
Для каждой системы управления, имеющей колебательный переходный процесс, на основе указанных критериев качества можно установить область допустимых отклонений управляемой величины.
При определении показателей качества в переходном режиме используются прямые и косвенные методы. Прямые методы предполагают вычисление функции 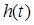 , ее построение и определение показателей качества по графику этой функции.
, ее построение и определение показателей качества по графику этой функции.
В косвенных методах оценки показателей качества получают на основе или коэффициентов характеристического уравнения системы, или корней этого уравнения, или на основе её передаточных функций, или её частотных характеристик, ряд методов ориентированы на применение вычислительных средств.
Для количественной оценки быстродействия систем используется также понятие степени устойчивости h, равное положительному числу, соответствующему расстоянию от мнимой оси до ближайшего к ней корня pi.
Для типовых систем δ =0,05 и тогда время переходного процесса составляет:
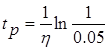 ,
,
Пример. Оценить время регулирования и перерегулирование для системы с передаточной функцией k/(s + 2).
Поскольку полюс p = -2 действительный, без мнимой части, колебаний не будет и перерегулирование σ = 0.
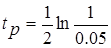 = 1,498 с.
= 1,498 с.
К косвенным методам оценки качества САР относятся нашедшие широкое распространение частотные методы (суждение о качестве по частотным характеристикам). Другими словами, в косвенных методах предполагается определение показателей качества переходного процесса системы без построения её переходной функции. Некоторые из этих косвенных методов рассматриваются ниже.
Оценки качества САУ по частотным характеристикам [57]
Математической основой частотного метода анализа качества автоматических систем является преобразование Фурье. Этот метод сочетает аналитические вычисления и графические построения.
Так как при анализе качества управления применяются те же частотные характеристики, что и при исследовании устойчивости, то частотный метод представляет собой единый метод анализа динамики автоматических систем. При этом используется аналитическая зависимость между переходной и частотной функциями замкнутой системы.
Переходная характеристика замкнутой САУ может быть определена по вещественной частотной характеристике (ВЧХ) P(w) из выражения
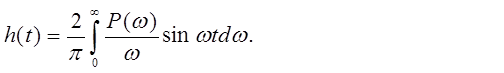 |
(6.5)
Для того чтобы косвенно (без построения кривой процесса) судить о качестве переходного процесса, надо рассмотреть свойства ВЧХ и соответствующих им переходных характеристик, устанавливаемые этой формулой. Приведем основные свойства:
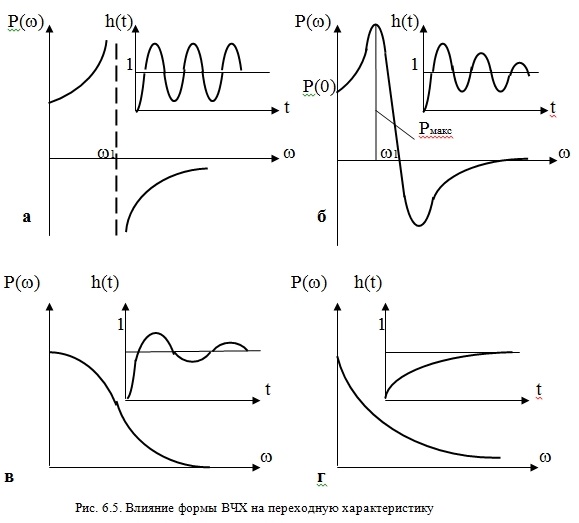
1. Если у ВЧХ есть разрыв непрерывности (Р(w1) = µ, как это показано на рис. 6.5,а, то характеристическое уравнение имеет мнимый корень pi = ±jw1 и в системе устанавливаются незатухающие колебания.
2. Высокий и острый пик ВЧХ, за которым Р(w) переходит через нуль при частоте, близкой к w1, соответствует медленно затухающим колебаниям (рис. 6.5,б).
3. Чтобы у h(t) было перерегулирование, не превышающее 18%, ВЧХ должна быть положительной невозрастающей функцией частоты w (рис. 6.5,в).
4. Чтобы h(t) была монотонной, ВЧХ должна быть положительной непрерывной функцией частоты с отрицательной убывающей по абсолютной величине производной (рис. 6.5,г).
Максимальное значение перерегулирования определяется по выражению (рис. 6.5,б)
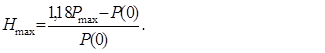 |
(6.7)
О качестве переходного процесса можно судить также по виду относительной АЧХ [40] в виде зависимости отношения H(ω)/К от частоты ω: Δ(ω) = H(ω)/К:
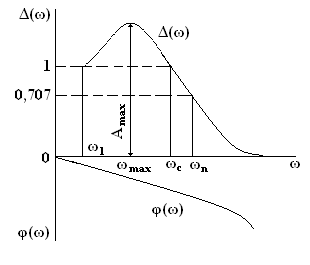
Рис.6.6.
Относительная АЧХ на резонансной частоте ωmax имеет максимум, соответствующий значению Δ(ωmax) = Δmax. При дальнейшем увеличении частоты система вследствие своей инерционности не успевает реагировать на колебания -больших частот и Δ(ω) резко «падает».
Пик характеристики является косвенной оценкой величины перерегулирования и колебательности процесса.
Установлено, что чем больше Δmax, тем более колебательным является переходной процесс.
Т.о. показатель колебательности можно определить по АЧХ замкнутой системы.
Отношение Δmax/Δ(0) = М называют показателем колебательности. То есть он равен максимальному значению ординаты АЧХ при начальной ординате, равной единице.
Для следящих систем Δ(0) = 1, поэтому М = Δmax. Обычно М = 1,2 – 1,5. При малых М система имеет большое время регулирования. При больших М увеличивается перерегулирование и система приближается к границе устойчивости.
Кроме частоты ωmax, характерными частотами АЧХ являются частота среза ωс и полоса пропускания ωп. Частота среза замкнутой системы ωс определяется на уровне Δ(ω) = 1. Для следящих систем частота среза определяет диапазон вынужденных колебаний, которые система пропускает без ослабления. На этой частоте амплитуды входного и выходного колебаний равны. Эта частота косвенным путем характеризует время переходного процесса. Можно сказать, что частота среза ωс является одним из частотных показателей замкнутой системы, определяемый по АЧХ разомкнутой системы.
При этом для монотонного (апериодического) процесса время регулирования: tр»p /wс. Чем больше частота среза, тем меньше время tр.
Полоса пропускания ωп замкнутой системы определяется на уровне Δ(0)/√2 = 0,707. Так как в диапазоне частот (ωс – ωп) АЧХ резко «падает», то числовые значения частот ωс и ωп близки.
Полоса пропускания влияет на точность и быстродействие системы. С увеличением полосы пропускания быстродействие системы растет. Чем больше полоса пропускания, тем больший спектр частот входного сигнала передается без искажений.
