И построения графика функции

Исследование функции 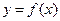целесообразно вести в определенной последовательности.

Примерный план исследования функции

1) Находим область определения функции.

2) Исследуем функцию на периодичность; четность или нечетность.

3) Находим (если это возможно) точки пересечения с осями координат.

4) Исследуем функцию на монотонность и точки экстремума.

5) Находим промежутки выпуклости, вогнутости и точки перегиба.

6) Находим асимптоты графика функции.

7) Для уточнения хода графика функции (если в этом есть необходимость) находим дополнительные точки.

8) По полученным данным строим график функции.

Пример 5.6. Дана функция 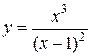. Провести полное исследование функции и построить ее график.

Решение. 1) Находим область определения функции.

В точке 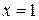функция не определена. Тогда область определения данной функции

.

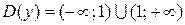2) Функция не является периодической.

Так как область определения функции не симметрична относительно начала координат, то это функция общего вида, следовательно, функция ни четная, ни нечетная.

3) Найдем точки пересечения графика функции с осями координат.

Для точек оси 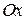выполняется условие: 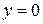. Решаем уравнение :

,

, ,

, ,

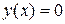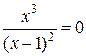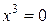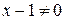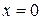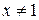Для точек оси 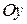находят значение функции в точке 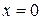. Для данной функции .

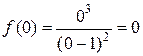Таким образом, единственной точкой пересечения графика функции с осями координат является начало системы координат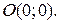

4) Находим промежутки возрастания и убывания функции, точки экстремума.

Выше нашли производную данной функции в общем виде:

.

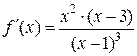Находим критические точки. Решаем уравнение :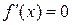

,

, ,

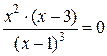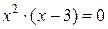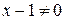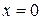или , ,

.

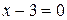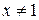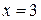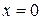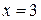Итак, получаем три критические точки: две и , в которых производная существует, и одну точку 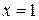, в которой производная функции не существует.

На числовой оси 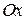отмечаем критические точки, и определяем знак первой производной на каждом промежутке:

На интервалах 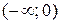, , 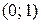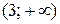функция возрастает, т.к. 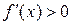. На интервале 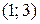функция убывает, т.к. .

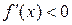При переходе через точку 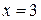производная 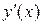изменяет знак с « 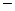» на « 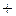», следовательно, в этой точке функция имеет минимум, причем 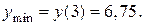В точках 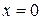и 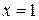экстремума нет.

5) Находим вторую производную функции :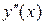

.

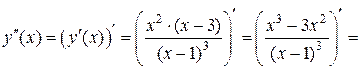
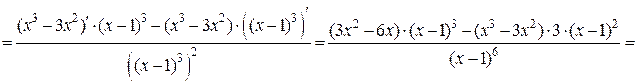
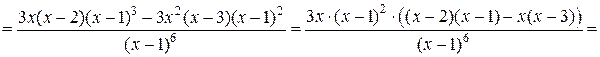
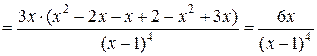Далее найдем точки, в которых 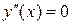или не существует:

,

, ,

, .

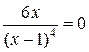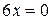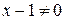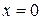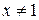На числовой оси 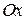отмечаем точки, и определяем знак второй производной на каждом промежутке:

На интервале 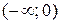график функции выпуклый, т.к. 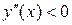. На интервалах 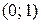и 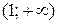график функции вогнутый, т.к. .

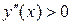При переходе через точку 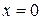производная 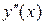изменяет знак с « 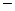» на « 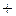», следовательно, эта точка является точкой перегиба. Точка 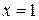не является точкой перегиба.

6) а) Функция терпит разрыв в точке 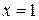. Найдем левосторонний и правосторонний пределы функции:

;

.

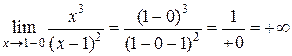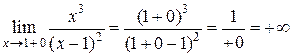Точка 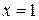- есть точка разрыва второго рода. Следовательно, прямая 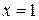является вертикальной асимптотой.

б) Уравнение наклонной асимптоты имеет вид: 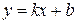. Коэффициенты 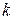и 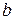находятся по следующим формулам:

; .

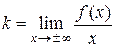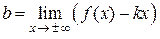Находим коэффициенты 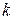и :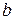

;

.

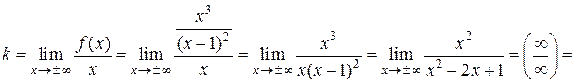
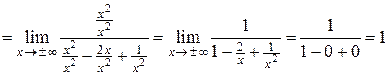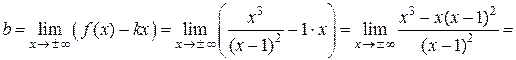
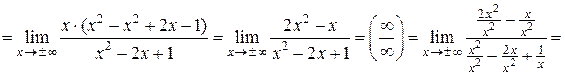
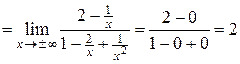Таким образом, прямая 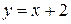является наклонной асимптотой.

7) Для уточнения графика функции найдем дополнительные точки:

; ;

; ;

.

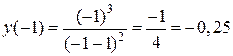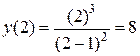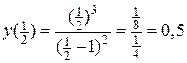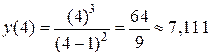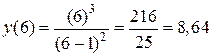8) Строим график функции.

,
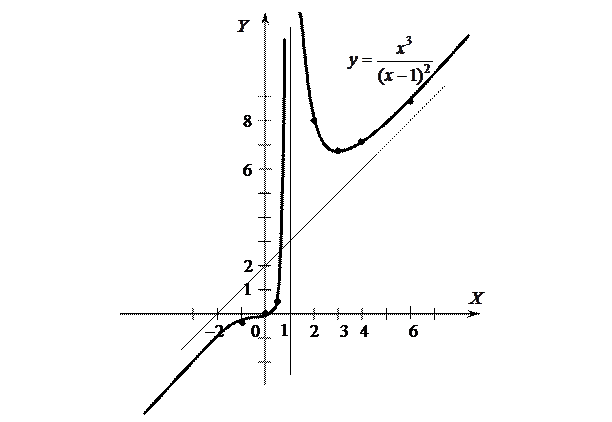