Производная сложной и обратной функций
Нахождение производной функции непосредственно по определению часто связано с определенными трудностями. На практике функции дифференцируют с помощью ряда правил и формул.
Теорема 3.2. Если функции 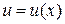 и
и 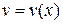 дифференцируемы в точке x, то функции
дифференцируемы в точке x, то функции 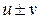 ,
, 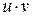 и
и 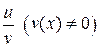 дифференцируемы в этой точке, причем:
дифференцируемы в этой точке, причем:
1) 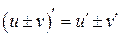 ;
;
2) 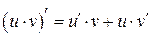 , в частности
, в частности 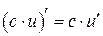 , где
, где 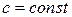 ;
;
3) 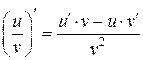 .
.
Следующие теоремы примем без доказательства.
Теорема 3.3. Если функция 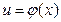 имеет в некоторой точке
имеет в некоторой точке  производную
производную 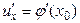 , а функция
, а функция 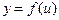 имеет в соответствующей точке
имеет в соответствующей точке 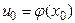 производную
производную 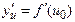 , то сложная функция
, то сложная функция 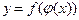 имеет производную
имеет производную 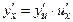 в точке
в точке  .
.
Теорема 3.4. Если функция 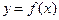 строго монотонна на интервале
строго монотонна на интервале 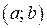 и имеет неравную нулю производную
и имеет неравную нулю производную 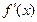 в произвольной точке этого интервала, то обратная ей функция
в произвольной точке этого интервала, то обратная ей функция 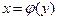 также имеет производную
также имеет производную 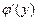 в соответствующей точке, определяемую равенством
в соответствующей точке, определяемую равенством
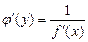 .
.
Пример 3.2. Найти производные следующих функций:
1) 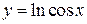 ; 2)
; 2) 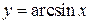 .
.
Решение. 1) Данная функция является сложной, т.е. 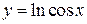 Û
Û 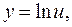
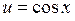 . Тогда, согласно теореме 3.3. получаем
. Тогда, согласно теореме 3.3. получаем
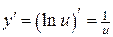 ,
, 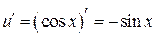 .
.
Следовательно, 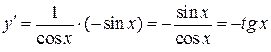 .
.
Решение можно записать и так:
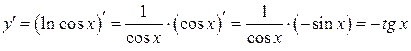 .
.
2) Для функции 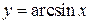 обратной является функция
обратной является функция 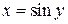 . Используя теорему 3.4., получаем
. Используя теорему 3.4., получаем
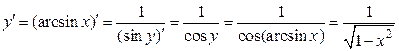 .
.
,
3.5.Таблица производных функций
На основе определения 3.1., а также теорем 3.2. – 3.4. можно записать таблицу производных элементарных функций:
1. 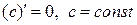 ; 7.
; 7. 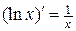 ; 13.
; 13. 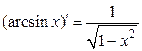 ;
;
2. 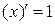 ; 8.
; 8. 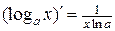 ; 14.
; 14. 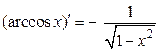 ;
;
3. 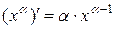 ; 9.
; 9. 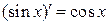 ; 15.
; 15. 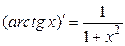 ;
;
4. 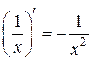 ; 10.
; 10. 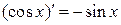 ; 16.
; 16. 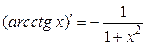 .
.
5. 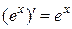 ; 11.
; 11. 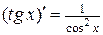 ;
;
6. 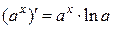 ; 12.
; 12. 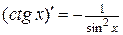 ;
;
В математике, механике, электротехнике и некоторых других дисциплинах встречаются гиперболические функции, определяемые следующими формулами:
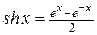 – гиперболический синус;
– гиперболический синус;
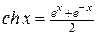 – гиперболический косинус («цепная линия»);
– гиперболический косинус («цепная линия»);
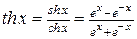 - гиперболический тангенс;
- гиперболический тангенс;
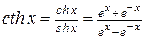 - гиперболический котангенс.
- гиперболический котангенс.
Найдем производную функции 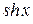 :
:
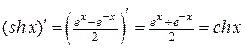 .
.
По налоги находим производные остальных гиперболических функций.
Таким образом,
17. 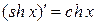 ; 19.
; 19. 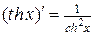 ;
;
18. 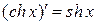 ; 20.
; 20. 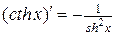 .
.
Поскольку на практике, приходиться работать со сложными функциями, то запишем таблицу производных соответствующим им сложных функций:
1. 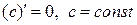 ; 8.
; 8. 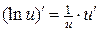 ; 14.
; 14. 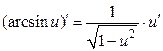 ;
;
2. 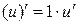 ; 9.
; 9. 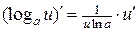 ; 15.
; 15. 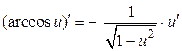
3. 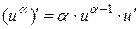 ; 10.
; 10. 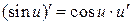 ; 16.
; 16. 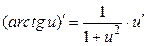 ;
;
4. 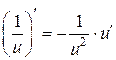 ; 11.
; 11. 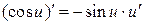 ; 17.
; 17. 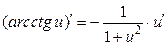 ;
;
5. 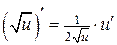 ; 12.
; 12. 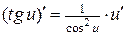 ; 18.
; 18. 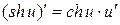 ;
;
6. 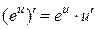 ; 13.
; 13. 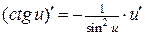 ; 19.
; 19. 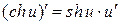 ;
;
7. 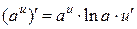 ; 20.
; 20. 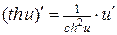 ;
;
21. 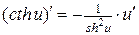 .
.
Пример 3.3. Найти производную следующей функции:
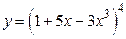 .
.
Решение. Используя таблицу производных и основные правила дифференцирования, получаем:
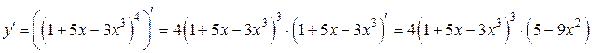 .
.
,
Пример 3.4. 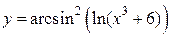 .
.
Решение. Проведем анализ структуры сложной функции:
1. 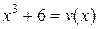 ;
;
2. 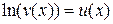 ;
;
3. 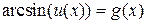 ;
;
4. 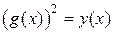 .
.
Для нахождения производной данной функции воспользуемся таблицей производных и правилами дифференцирования.
Дифференцирование сложной функции выполняется в следующей последовательности:
1. 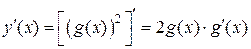 ;
;
2. 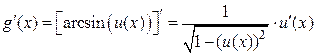 ;
;
3. 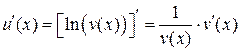 ;
;
4. 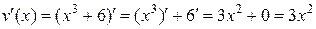 .
.
Теперь весь процесс дифференцирования данной функции можно записать следующим образом:
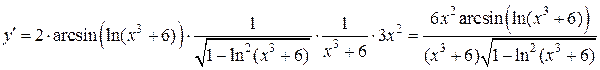 .
.
,
3.6.Дифференцирование функций, заданных неявно
Функции, которые рассматривались выше, были представлены в виде  , т.е. переменная y выражалась через переменную x.
, т.е. переменная y выражалась через переменную x.
Если функция задана уравнением  , разрешенным относительно y, то функция задана в явном виде (явная функция). Например,
, разрешенным относительно y, то функция задана в явном виде (явная функция). Например, 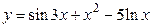 ,
, 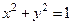 задает две функции
задает две функции 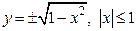 .
.
Во многих задачах приходиться сталкиваться с ситуацией, когда переменную y невозможно выразить через x. Например, 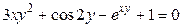 . В этих случаях функция записывается в виде
. В этих случаях функция записывается в виде 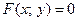 , и говорят, что она задана неявно.
, и говорят, что она задана неявно.
Под неявным заданием функции понимают задание функции в виде уравнения 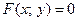 , не разрешенного относительно y.
, не разрешенного относительно y.
Чтобы найти производную функции, которая задана уравнением 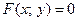 (задана неявно), достаточно продифференцировать это уравнение по x, рассматривая при этом y как функцию x, и полученное затем уравнение разрешить относительно
(задана неявно), достаточно продифференцировать это уравнение по x, рассматривая при этом y как функцию x, и полученное затем уравнение разрешить относительно 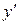 .
.
Производная неявной функции выражается через аргумент x и функцию y.
Пример 3.5. Найти производную функции, заданной неявно:
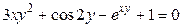 .
.
Решение. Дифференцируем обе части данного уравнения, считая y функцией от x. Получаем
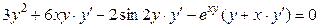 ;
;
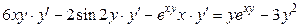 ;
;
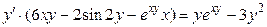
Отсюда находим
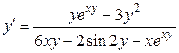 . ,
. ,
Чтобы найти производную функции, заданную уравнением 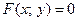 , где y – функция независимой переменной x, то можно воспользоваться следующей формулой:
, где y – функция независимой переменной x, то можно воспользоваться следующей формулой:
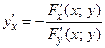 .
.
Пример 3.5 (2). Найти производную функции, заданной неявно:
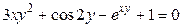 .
.
Решение. Находим 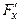 и
и 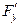 .
.
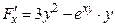 ;
; 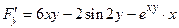 .
.
Затем находим
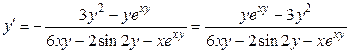 .
.
,
Пример 3.6. Найти значение производной функции в точке 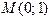 , если
, если
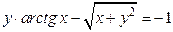 .
.
Решение. Дифференцируем обе части данного уравнения, считая y функцией от x. Получаем
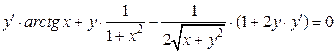 ;
;
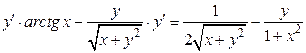 ;
;
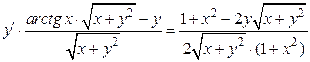 .
.
Отсюда находим
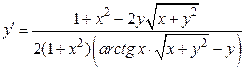 .
.
Далее
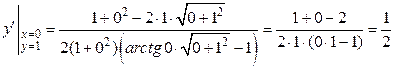 .
.
,
Дифференцирование функций,
Заданных параметрически
Кроме того, что функция может быть задана в явном или неявном виде, есть функции, которые можно задать параметрически.
Если зависимость между аргументом x и функцией y задана в виде уравнений
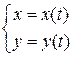 ,
,
где t – вспомогательная переменная, называемая параметром, то говорят, что «функция задана параметрически».
Например, 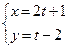 задает линейную функцию
задает линейную функцию 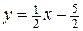 , которую можно получить, если из первого уравнения выразить t и подставить во второе.
, которую можно получить, если из первого уравнения выразить t и подставить во второе.
Теорема 3.5. Пусть функция задана параметрически
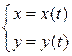 ,
,
и функции 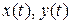 дифференцируемы в области определения переменной t, тогда
дифференцируемы в области определения переменной t, тогда
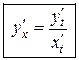 . (3.3)
. (3.3)
Пример 3.7. Пусть 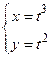 . Найти
. Найти 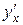 .
.
Решение. Имеем 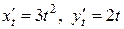 .
.
Следовательно, 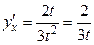 .
.
,
В этом можно убедиться, если найти непосредственно зависимость y от x. Действительно, 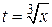 . Тогда
. Тогда 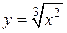 . Отсюда
. Отсюда 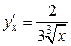 , т.е.
, т.е. 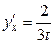 .
.
Пример 3.8. Пусть 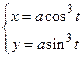 . Найти
. Найти 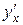 в точке
в точке 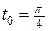 .
.
Решение. Используя формулу (3.3), находим
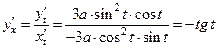 .
.
Далее получаем
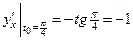 .
.
,
3.8. Производные высших порядков
Производная 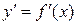 функции
функции  есть также функция от x и называется производной первого порядка.
есть также функция от x и называется производной первого порядка.
Если функция 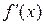 дифференцируема, то ее производная называется производной второго порядкаи обозначается:
дифференцируема, то ее производная называется производной второго порядкаи обозначается: 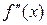 или
или 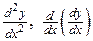 . Итак,
. Итак,
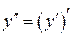 .
.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается: 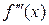 или
или 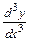 . Итак,
. Итак,
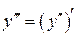 .
.
Производная n-го порядка (или n-й производной) называется производная от производной 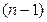 порядка:
порядка:
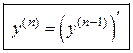 . (3.4)
. (3.4)
Производная порядка выше первого называются производными высших порядков. Начиная с производной четвертого порядка, производные обозначаются римскими цифрами или числами в скобках, например, 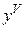 или
или 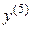 – производная пятого порядка.
– производная пятого порядка.
Пример 3.9. Найти значение производной 4-го порядка для функции
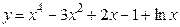 при
при 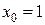 .
.
Решение. Находим последовательно
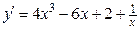 ;
;
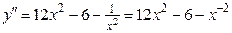 ;
;
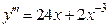 ;
;
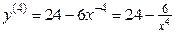 .
.
Следовательно, 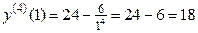 .
.
,
Пример 3.10. Найти производную n-го порядка для функции 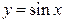 .
.
Решение. Находим последовательно
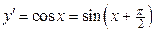 ;
;
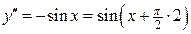 ;
;
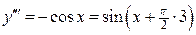 ;
;
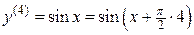 ;
;
…………………….
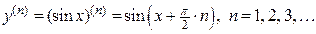 . ,
. ,
Отметим, что в формуле (3.4) принято 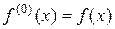 , т.е. производная нулевого порядка есть сама функция.
, т.е. производная нулевого порядка есть сама функция.
Пусть материальная точка движется прямолинейно по закону 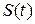 . Как известно, производная первого порядка
. Как известно, производная первого порядка 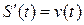 .
.
Механический смысл производной второго порядка: вторая производная от пути по времени есть величина ускорения прямолинейного движения материальной точки, т.е. 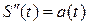 .
.
Пусть функция  задана неявно в виде уравнения
задана неявно в виде уравнения 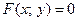 .
.
Продифференцировав это уравнение по x, и разрешив полученное уравнение относительно 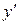 , найдем производную первого порядка. Продифференцировав по x первую производную, получим вторую производную от неявной функции. В нее войдут x, y и
, найдем производную первого порядка. Продифференцировав по x первую производную, получим вторую производную от неявной функции. В нее войдут x, y и 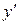 . Подставляя уже найденное значение
. Подставляя уже найденное значение 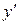 в выражение второй производной, выразим
в выражение второй производной, выразим 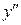 через x и y.
через x и y.
Аналогично поступаем для нахождения производной третьего (и выше) порядка.
