Регрессионный анализ зависимости высот и диаметров в чистом сосновом древостое с помощью ПЭВМ
Анализ зависимости между случайными величинами с помощью линейного регрессионного анализа в пакете Statistica 6.0 можно выполнить следующим образом.
1. Запустить программу Statistica и открыть файл с данными, как описано в подразделе 2.4.
2. Выбрав опцию «Множественная регрессия» из меню «Статистика», открыть диалоговое окно «Multiple Linear Regression».
3. В открывшемся диалоговом окне нажать кнопку «Variables». После этого на экране появится еще одно диалоговое окно «Select dependent and independent variable lists», содержащее два списка переменных. Из левого списка следует выбрать зависимую переменную (переменную, которая в уравнении стоит слева от знака равенства). В правом списке надо отметить независимые переменные, для которых желательно построить регрессионное уравнение (переменные, которые будут справа от знака равенства). Выбрать сразу несколько переменных можно мышью, держа нажатой клавишу «Ctrl» на клавиатуре. Кроме того, номера независимых переменных можно перечислить в строке, расположенной под списком переменных с помощью клавиатуры, отделяя номера друг от друга пробелом или указывая первый и последний номер переменной через тире, если номера идут подряд. Далее надо нажать кнопку «ОК» для возврата в окно «Multiple Linear Regression».
4. Для того чтобы выполнить вычисления в окне «Multiple Linear Regression», надо нажать кнопку «ОК», в результате чего откроется диалоговое окно «Multiple Regression Results». В данном окне приведены значения некоторых статистик, характеризующих полученное уравнение. Это коэффициент корреляции R; коэффициент детерминации 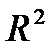 ; преобразованный коэффициент детерминации adjusted R2; стандартная ошибка - std. error и критерий Фишера F.
; преобразованный коэффициент детерминации adjusted R2; стандартная ошибка - std. error и критерий Фишера F.
5. Чтобы увидеть вычисленные коэффициенты регрессии и статистики, характеризующие их, следует нажать кнопку «Summary: Regression results» на вкладке «Quick» в окне результатов регрессионного анализа. На экране появится таблица, содержащая в первой колонке имена независимых переменных (Intercept- свободный член).
Колонка, озаглавленная как «Beta», содержит регрессионные коэффициенты, вычисленные с учетом предварительной нормировки переменных, а колонка «Std.Err. of Beta» - их стандартные ошибки.
Колонка «В» содержит коэффициенты регрессии, а колонка «Std. Err. of В» - их стандартные ошибки.
В колонке «t» приведены t-критерии Стьюдента, вычисленные для проверки параметрической гипотезы о равенстве коэффициент регрессии нулю. Если t-статистика превышает табличное значение для выбранного уровня значимости и соответствующего числа степеней свободы (указано в скобках в заголовке колонки после символа t), гипотеза отвергается.
Колонка «p-level» содержит вероятность того, что гипотеза о Равенстве коэффициента регрессии нулю верна.
В качестве примера проанализируем связь между высотами и диаметрами в чистом одновозрастном древостое. С этой целью выполним расчеты для регрессионных уравнений следующих видов:
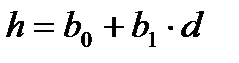 (30)
(30)
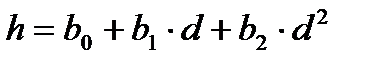 (31)
(31)
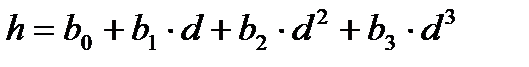 (32)
(32)
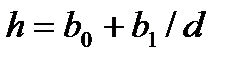 (33)
(33)
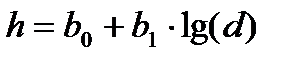 (34)
(34)
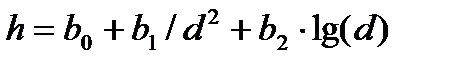 (35)
(35)
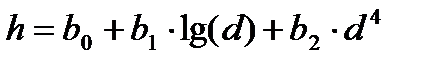 (36)
(36)
Для выполнения таких расчетов необходимо в файле исходных данных создать пять новых переменных. Для этого надо активизировать опцию «Добавить переменные ...» из меню «Вставка». В открывшемся диалоговом окне «Add Variables» в поле «How many» внести число переменных, которые следует добавить, и нажать кнопку «ОК». Далее нужно дать название добавленным переменным и вычислить их значения. Это можно сделать следующим способом. Щелчок правой кнопкой мыши на заголовке переменной открывает контекстное меню, из которого следует выбрать опцию «Variable Specs ...», которая откроет диалоговое окно свойств переменных. В этом окне следует изменить имя в поле «Name», а в текстовое поле, расположенное в нижней части диалогового окна, надо ввести формулу для вычисления значений переменной. Если в формуле необходимо использовать стандартные функции, целесообразно воспользоваться кнопкой «Functions», которая открывает список доступных функций. Кроме того, с помощью данного диалогового окна можно изменить и другие свойства переменной. После нажатия кнопки «ОК» все изменения будут выполнены, а если вводилась формула, то будут вычислены и значения переменной. Таким образом, надо создать переменные 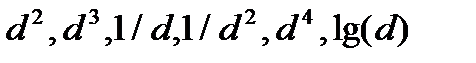 .
.
После этого можно выполнить расчеты для уравнений вида (30)-(36). Полученные результаты удобно свести в табл. 19.
В данной таблице обращают на себя внимание два уравнения – парабола третьего порядка и гипербола второго порядка.
Таблица 19 ─ Статистические показатели, характеризующие уравнения регрессии
| Уравнение | Коэф-фици-ент коре-ляции R | Коэф-фици-ент детер-мина-ции 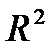 | Преобразо-ванный Коэффици-ент детермина-ции 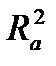 | Крите-рий Фишера F | Стан-дартная ошибка оценки 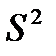 |
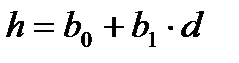 | 0,720 | 0,518 | 0,516 | 212,84 | 1,59 |
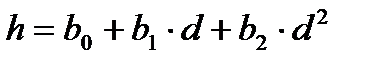 | 0,767 | 0,588 | 0,585 | 140,98 | 1,47259 |
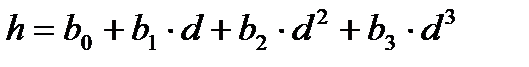 | 0,774 | 0.599 | 0,593 | 97,682 | 1,45733 |
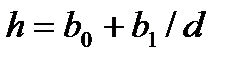 | 0,772 | 0,596 | 0,594 | 292,61 | 1,45733 |
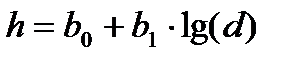 | 0,755 | 0.570 | 0,568 | 262,53 | 1,50177 |
Таблица 20 ─ Параметры регрессионного уравнения
| N=200 | Beta | Std.Err of Beta | B | Stg.Err of B | t(197) | p-level |
| Intercept | 31,320 | 0,41528 | 75,4186 | 0,000000 | ||
| D | -0,7722 | 0,045147 | -199,738 | 11,67664 | -17,1058 | 0,000000 |
Полученное нами уравнение гиперболы выглядит следующим образом:
h 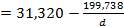
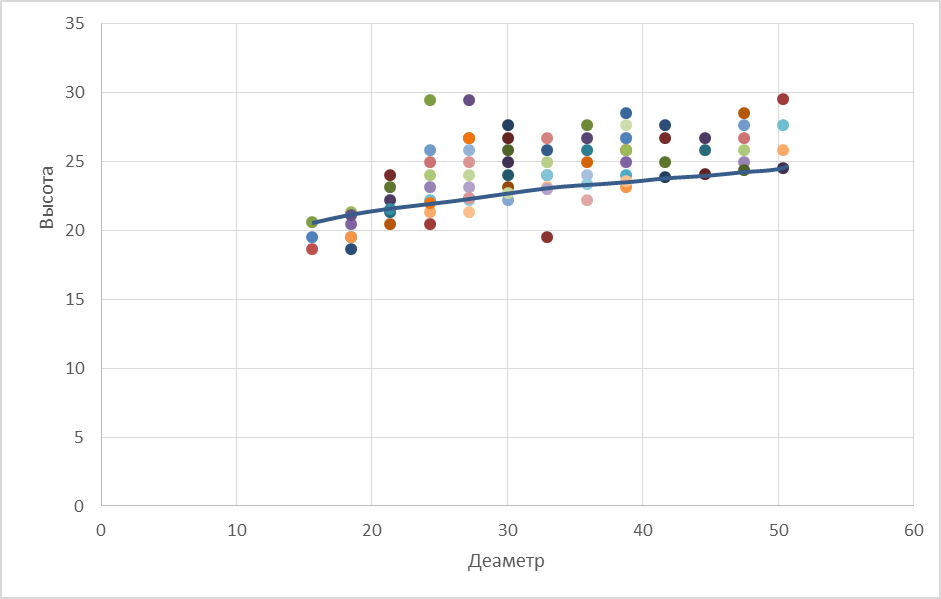
Рисунок 5,3 ─ Парабола третьего порядка
