Оценка коэффициентов параболы второго порядка

Оценку коэффициентов параболы второго порядка методом наименьших квадратов дает решение системы нормальных уравнений:

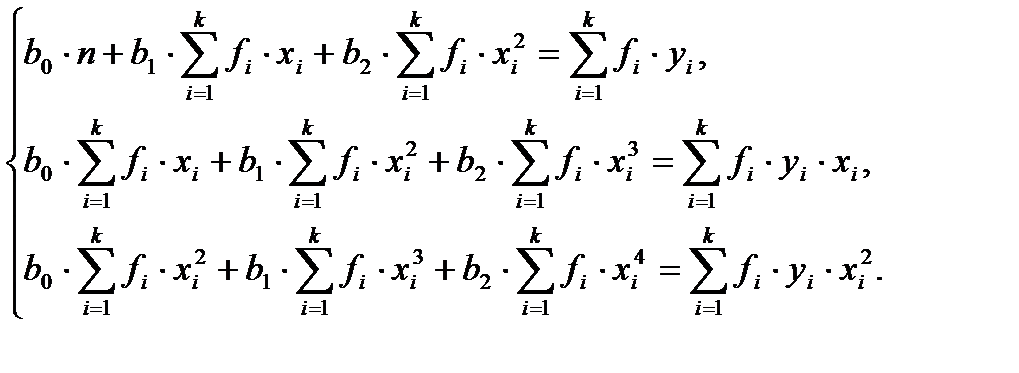(18)

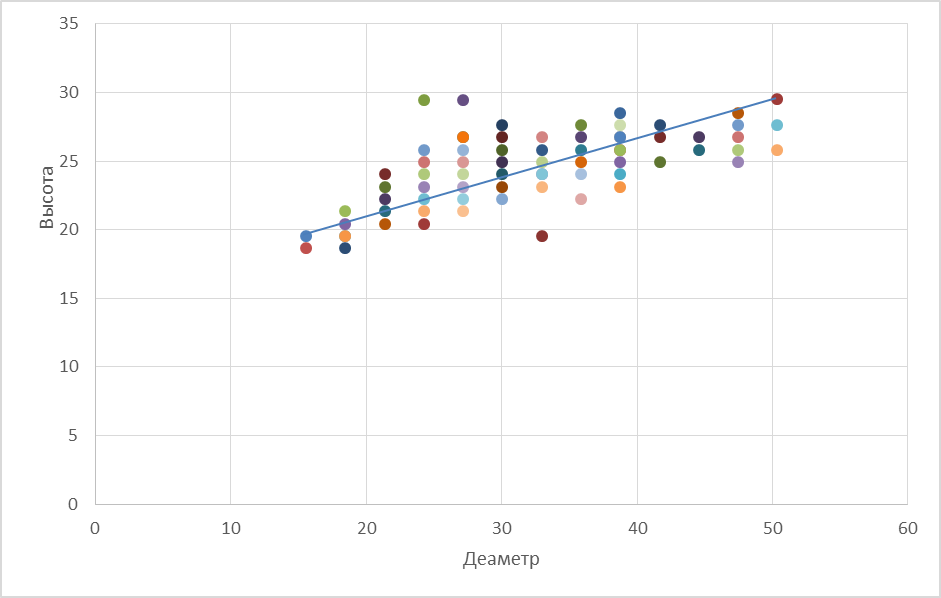
Рисунок 5,1 ─ Зависимость между высотами и диаметрами деревьев в древостое (прямая)

Вычислим коэффициенты уравнения параболы второго порядка, описывающей связь высот и диаметров деревьев в древостое. Для выполнения вычислений составим вспомогательную таблицу, анало­гичную той, которую составляли для регрессионного уравнения пря­мой (табл. 20). Подставив найденные значения в систему нормальных уравнений (18), получим

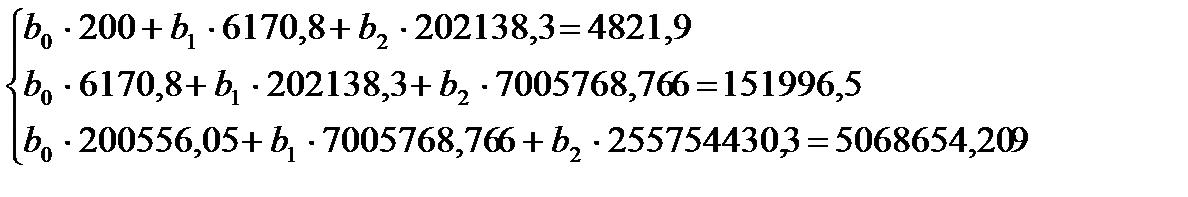(19)

Найдем решение системы нормальных уравнений (19). Сначала разделим все уравнения системы на коэффициенты при параметре :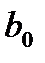

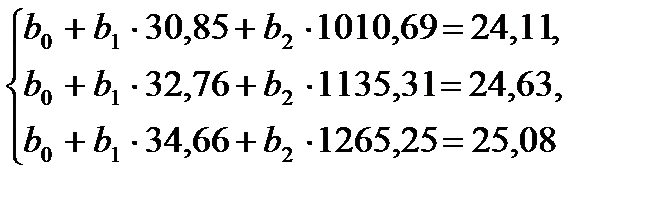(20)

Таблица 18 ─

H\D	15,6	18,5	21,4	24,3	27,2	30,1		35,9	38,8	41,7	44,6	47,5	50,4	Всего	fi*yi
29,4															58,8
28,5
27,6															331,2
26,7															667,5
25,8
24,9															647,4
23,1															438,9
22,2															355,2
21,3															149,1
20,4
19,5
18,6															55,8
fx															4821,9
∑fi*xi	46,8	129,5	385,2	656,1	870,4	933,1		861,6	698,4	250,2	178,4	332,5	201,6	6170,8
∑fi*xi2	730,08	2395,75	8243,28	15943,23	23674,88	28086,31		30931,44	27097,92	10433,34	7956,64	15793,75	10160,64	202138,26
∑fi*xi3	11389,248	44321,375	176406,192	387420,489	643956,736	845397,931		1110438,696	1051399,296	435070,278	354866,144	750203,125	512096,256	7005768,766
∑fi*xi4	177672,2688	819945,4375	3775092,51	9414317,88	17515623,22	25446477,72		39864749,19	40794292,68	18142430,59	15827030,02	35634648,44	25809651,3	255754430,3
∑fij*yj*xi	898,56	1820,4	8076,36	14900,76	21232,32	23071,65	15701,4	22229,28	18263,16	6642,81	4723,14	8963,25	5473,44	151996,53
∑fij*yj*xi2	14017,536	33677,4	172834,104	362088,468	577519,104	694456,665	518146,2	798031,152	708610,608	277005,177	210652,044	425754,375	275861,376	5068654,209
y̅i	16,62	18,72	20,57	22,18	23,56	24,69	25,59	26,24	26,65	26,83	26,76	26,45	25,91
∑fij*(yi-i˜)2	20,48	10,15	62,98	137,23	112,97	46,07	51,41	33,80	32,33	4,38	0,94	11,02	8,60	532,36

Теперь вычтем первое уравнение системы (20) из второго, а второе -из третьего. В результате получим систему из двух уравнений:

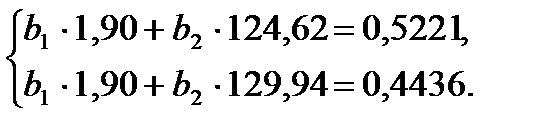(21)

Теперь вновь разделим уравнения системы (21) на коэффициент, на этот раз при параметре :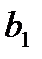

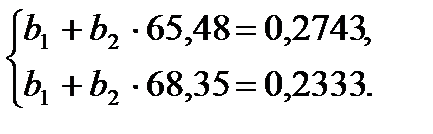(22)

Вычитая первое уравнение системы (45) из второго, получим

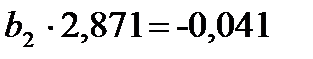(23)

откуда нетрудно выразить параметр :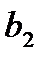

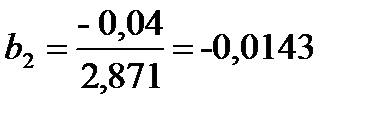(24)

Подставив полученное значение параметра 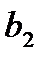в первое уравнение системы (24), выразим из него и вычислим величину параметра :

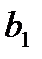b₁ 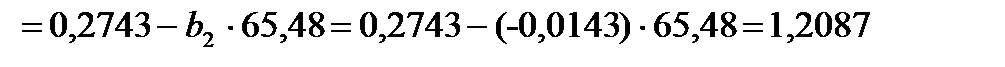(25)

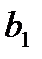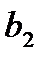Теперь, воспользовавшись первым уравнением из системы (23), а также значениями параметров и , вычислим величину :

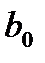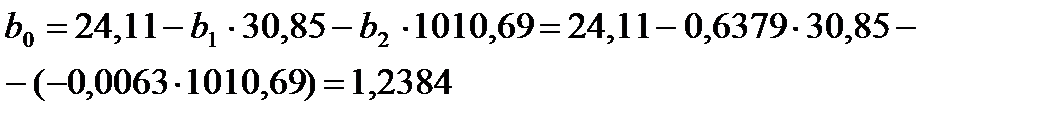(26)

В результате выполненных вычислений мы получили регресси­онное уравнение параболы второго порядка, описывающее зависи­мость высоты от диаметра в чистом сосновом древостое:

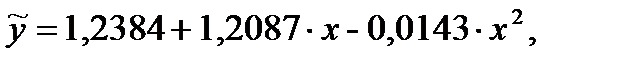(27)

или, с использованием других обозначений:

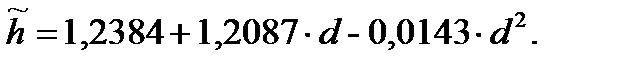(28)

С помощью полученного уравнения регрессии определим тео­ретические высоты 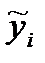и сумму квадратов отклонений эмпирических высот от теоретических (табл. 20). Используя сумму квадратов откло­нений 532,36, мы можем вычислить стандартную ошибку регрессион­ного уравнения параболы второго порядка:

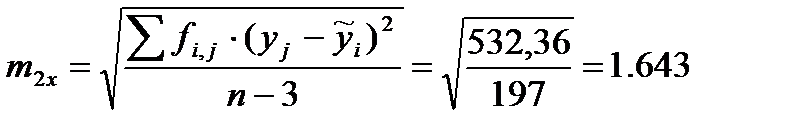(29)

На рис. 5 изображено полученное регрессионное уравнение параболы второго порядка.

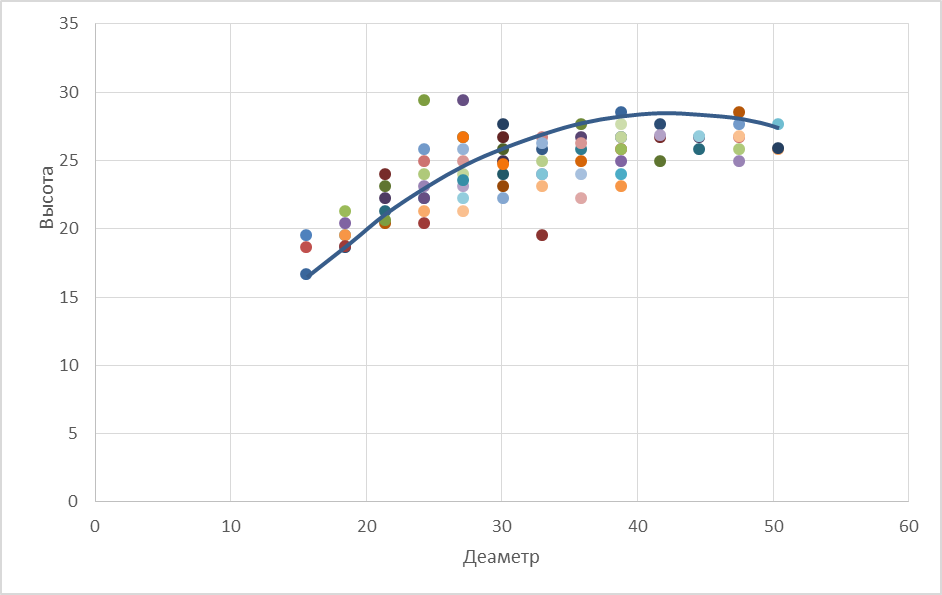
Рисунок 5,2 ─Зависимость между высотами и диаметрами деревьев в древостое (парабола второго порядка)