Системы линейных уравнений. Правило Крамера. Метод Гаусса. Матричный способ

Пример 1. Решить систему:

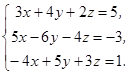
1-й способ. По формулам Крамера:

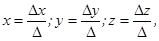
где 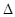-главный определитель системы, столбцы которого есть коэффициенты при неизвестных

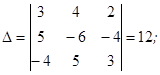
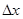-вспомогательный определитель, который получается из главного заменой 1-го столбца (коэффициентов при x) столбцом свободных членов.

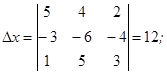
Аналогично получаем 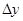и :

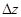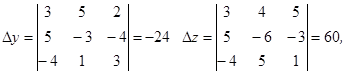
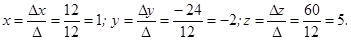
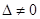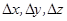Если , то система имеет единственное решение, если , а хотя бы один из не равен 0, то система не имеет решений. Если 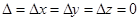, то система имеет множество решений.

2-й способ. Метод Гаусса, или метод исключения неизвестных.

Рассмотрим сначала несколько понятий.

Определение. Рангом матрицы 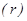называется наивысший порядок её минора, отличного от нуля.

Пример.

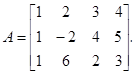
Вычислим все миноры третьего порядка:

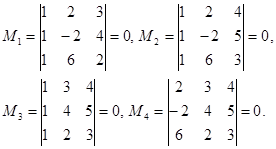
Вычислим минор второго порядка:

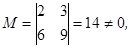
поэтому ранг матрицы A равен 2:

.

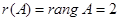Рассмотрим более простой способ вычисления ранга матрицы, основанный на приведении матрицы к ступенчатому виду.

Определение. Матрицу А называют ступенчатой, если

а) любая её строка имеет хотя бы один отличный от нуля элемент,

б) первый отличный от нуля элемент каждой её строки, начиная со второй, расположен правее неравного нулю элемента предыдущей строки.

Пример.

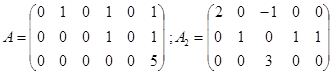
Определение. Элементарными преобразованиями матрицы называются следующие преобразования её строки:

а) перестановка двух каких-нибудь строк;

б) умножение элементов какой-либо строки на число, отличное от нуля;

в) прибавление к элементам какой-либо строки соответствующих элементов другой строки, умноженных на некоторое число.

Пример.

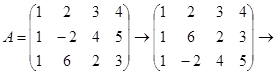
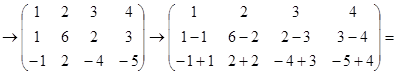
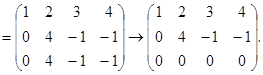
Из последней матрицы (ступенчатый вид) видно, что .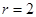

Приведем несколько утверждений без доказательств.

Теорема 1. При элементарных преобразованиях и отбрасывании нулевой строки ранг матрицы не изменяется.

Теорема 2. Всякую ненулевую матрицу можно привести к ступенчатому виду с помощью элементарных преобразований и выбрасывания нулевых строк.

Теорема 3. Ранг ненулевой матрицы равен числу строк её ступенчатого вида.

Рассмотрим систему:

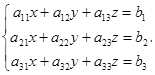
Определение. Матрица, составленная из коэффициентов при неизвестных системы, называется матрицей системы.

Определение. Матрица называется расширенной матрицей системы, если к матрице 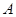присоединить столбец из свободных членов системы.

.

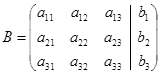Расширенная матрица- это закодированная запись системы. Строки матрицы соответствуют уравнениям системы. Умножение уравнения на число и сложение этого произведения с другим уравнением эквивалентно умножению строки матрицы на это число и почленному сложению произведения с другой строкой матрицы. Таким образом, работу с уравнениями мы можем заменить работой со строками матрицы.

Эффективным методом решения и исследования системы линейных уравнений является метод исключения неизвестных, называемый также методом Гаусса. Он состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему ступенчатого вида (или, в частности, треугольную систему), которая легко исследуется и решается. Применение метода Гаусса не зависит ни от числа уравнений, ни от числа неизвестных в системе.

Рассмотрим систему 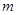линейных уравнений с 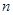неизвестными 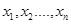,которую запишем в виде расширенной матрицы:

.

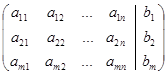Заметим, что иногда могут встречаться уравнения, все коэффициенты которых (т.е. соответствующая строка матрицы) равны 0:

.

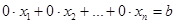Если в этом уравнении 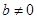, то ему, очевидно, не удовлетворяют никакие значения неизвестных, и система, содержащая хотя бы одно такое уравнение, несовместна, т.е. не имеет решения. Если же 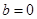, то ему удовлетворяют любые решения неизвестных, т.е. рассматриваемое уравнение является тождеством и его можно удалить из системы.

Элементарные преобразования матрицы, рассмотренные ранее, можно производить и над расширенной матрицей системы, поэтому в дальнейшем будем говорить об элементарных преобразованиях, не делая различий между уравнениями системы и строками расширенной матрицы.

Разберём идею метода Гаусса на конкретных примерах.

Пример 2.

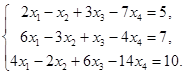
Решение.

I этап: запишем систему в виде расширенной матрицы

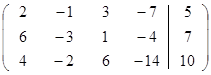
II этап: исключим с помощью первого уравнения x из остальных уравнений. Для этого домножим первую строку на –3 и сложим её со второй, затем умножим первую строку на –2 и сложим её с третьей.

Получим

.

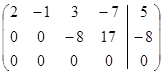Последняя строка состоит из нулей, если её расписать в виде уравнения, то получим

.

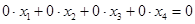Это уравнение является тождеством, поэтому его нет смысла оставлять в системе.

Раскодируем полученную матрицу:

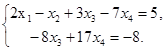
Выразим из второго уравнения :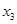

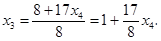
Подставим в первое уравнение вместо 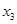его выражение через 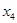и выразим :

,

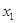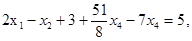
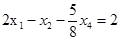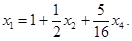
Ответ:

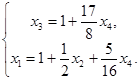
Получим так называемое общее решение системы, которое является формулой для получения конкретных её решений. Эти конкретные решения системы называются частными решениями. Получают их следующим образом: придавая переменным 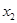, 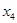произвольные значения и находя по этим значениям 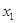и 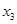, всякий раз находят решение системы. Так как 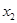и 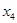можно придавать произвольные значения, то эти переменные называются свободными. Неизвестные 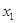и 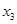, значения которых вычисляются по значениям 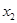и 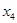, называются базисными.

Получим одно из частных решений в предыдущем примере. Пусть 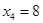, а 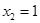, тогда , .

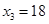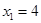Ответ: 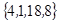-частное решение.

Пример 3.

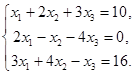
Решение.

Закодируем систему и приведем матрицу к треугольному виду

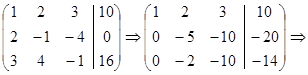
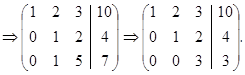
Таким образом, заданная система равносильна следующей:

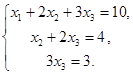
Находим 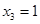из последнего уравнения, затем 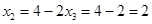из второго, и наконец, из первого:

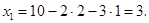
Ответ: .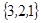

Пример 4.

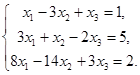
Выпишем расширенную матрицу и упростим её:

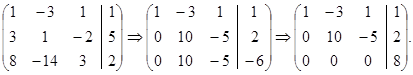
Полученная система

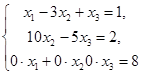
несовместна, так как её последнее уравнение не имеет смысла. Следовательно, исходная система также несовместна.