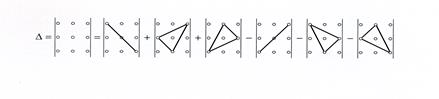Линейные операции над векторами и их свойства

Линейная алгебра

Определение. Матрицей А размера 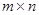называется таблица чисел, записанная в виде

.

Короче матрицу обозначают так:

.

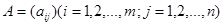Числа 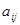называются элементами матрицы. Элементы матрицы образуют столбцы и строки. В обозначении элемента 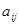первый индекс 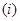указывает номер строки, а второй 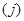- номер столбца, на пересечении которых стоит этот элемент.

Если в матрице число строк равно числу столбцов 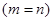, то матрица называется квадратной n-го порядка. Если же 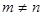, то матрица называется прямоугольной.

В матрице А m строк и n столбцов.

Если 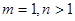, то получается однострочная матрица 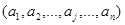, которая называется вектор-строкой.

Если же 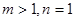, то получается одностолбцовая матрица

,

которая называется вектор-столбцом.

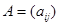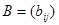Две матрицы: и называются равными, если равны элементы, стоящие на одинаковых местах, т.е. 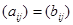, если 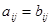при всех i,j (при этом число столбцов и строк матриц А и В должно быть одинаковым).

Матрицы можно складывать, умножать на число и друг на друга. Рассмотрим операции над матрицами.

Суммой двух матриц 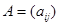и 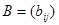одного размера 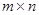называется новая матрица 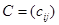того же размера 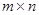, элементы которой определяются равенством

.

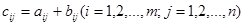Обозначение: A+B=C .

Пример 1.

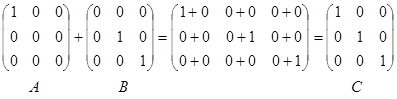
Аналогично определяется разность двух матриц.

Чтобы умножить матрицу 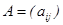на число l, нужно умножить на это число все элементы матрицы

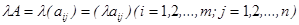
Пример 2.

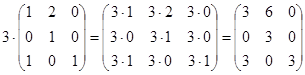
Произведение двух матриц.

Произведением матрицы 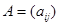размера 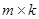(m строк, k столбцов) на матрицу 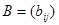размера 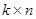(k строк, n столбцов) называется матрица 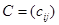размера 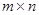(m строк, n столбцов), у которой элемент 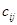равен сумме произведений элементов i-й строки матрицы А на j-й столбец матрицы В, т.е.

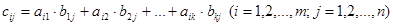
При этом число столбцов матрицы А должно быть равно числу строк матрицы В. В противном случае произведение матриц не определено.

Обозначение: .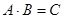

Пример 3.

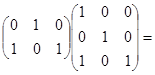
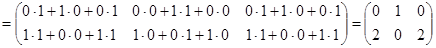
Пример 4.

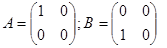
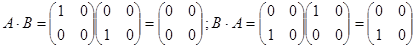
Отсюда видно, что 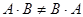,т.е. умножение матриц не перестановочно.

Легко проверить, что для суммы и произведения матриц справедливы следующие свойства.

1.

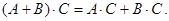
2.

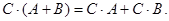
3.

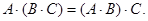
4.

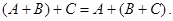
Единичная матрица.

Совокупность элементов 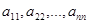квадратной матрицы 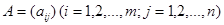называется главной диагональю матрицы.

Матрица, у которой элементы, стоящие на главной диагонали, равны единице, а все остальные элементы равны нулю, называется единичной матрицей и обозначается буквой E. Единичной матрицей 3-го порядка будет .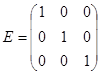

Произведение квадратной матрицы любого порядка на единичную матицу того же порядка не меняет данную матрицу.

Пример 5.

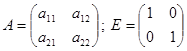
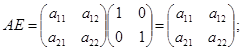
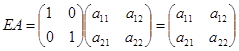
Очевидно, .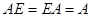

Определители и их свойства

Рассмотрим квадратную матрицу3-го порядка.

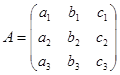
Определение. Определителем (или детерминантом) третьего порядка, соответствующим матрице А, называют число, обозначаемое символом

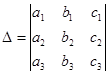
и определяемое равенством

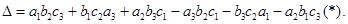
Числа 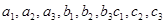называются элементами определителя. Диагональ, образованная элементами 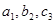называется главной , а диагональ, образованная элементами 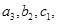-побочной.

Чтобы запомнить, какие произведения в правой части равенства (*) берутся со знаком +, а какие со знаком - , полезно пользоваться правилом треугольников.

Пример.

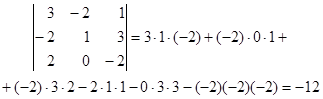
Замечание

Определителем 2-го порядка 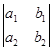, соответствующим матрице 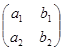, называется число, равное .

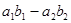Определение. Минором 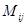элемента 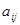определителя называется определитель, полученный из данного, вычеркиванием i-й строки и j-го столбца, на пересечении которых расположен этот элемент.

Алгебраическим дополнением 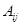элемента 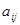называется минор этого элемента 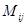, умноженный на 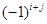, т.е.

.

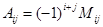Свойства определителей рассмотрим на примере определителей третьего порядка.

1. Величина определителя не изменится, если строки и столбцы определителя поменять местами.

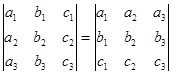
2. При перестановке двух рядом стоящих строк (или столбцов) определителя знак определителя меняется на противоположенный, т.е.

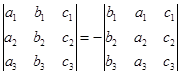
3. Если определитель имеет два одинаковых столбца или две одинаковых строки, то он равен нулю.

4. Общий множитель всех элементов некоторого столбца (или строки) выносится за знак определителя

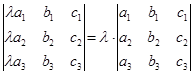
5. Если все элементы столбца (строки) равны нулю, то определитель равен нулю.

6. Если элементы двух столбцов (строк) определителя пропорциональны, то определитель равен нулю.

7. Если каждый элемент некоторого столбца (строки) есть сумма двух слагаемых, то определитель равен сумме двух определителей: в одном на месте суммы стоит первое слагаемое, в другом –второе.

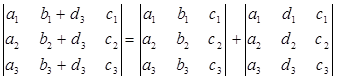
8. Если к элементам некоторого столбца (строки) определителя прибавить соответствующие элементы другого столбца (строки), умноженные на одно и то же число, то определитель при этом не изменится.

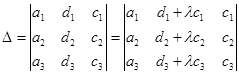
9. Определитель равен сумме произведений элементов какого-нибудь столбца (строки) на их алгебраические дополнения.

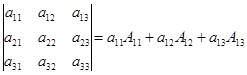
Представление определителя в соответствии со свойством 9 называется разложением определителя по элементам некоторого столбца (строки).

10. Сумма произведений элементов какого-нибудь столбца (строки) на алгебраическое дополнение соответствующих элементов другого столбца (строки) равна нулю.

Пример.

Вычислить определитель, разлагая его по элементам первой строки.

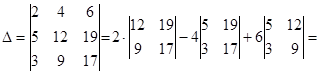
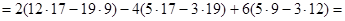
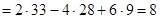
Векторная алгебра

Прямоугольная система координат в пространстве определяется заданием единицы измерения длины и трёх пересекающихся в одной точке взаимно перпендикулярных осей: Ox,Oy, и Oz.

Точка - начало координат, Ox- ось абсцисс, Oy-ось ординат,

Oz – ось аппликат.

Пусть М- произвольная точка пространства (рис. 1.1). Проведем через точку М три плоскости, перпендикулярные координатным осям Ox, Oy, и Oz. Точка пересечения построенных плоскостей обозначается через 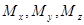соответственно.

Прямоугольными координатами точки М называются числа

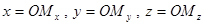
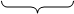
При этом называют - абсциссой, 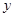– ординатой, 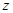– аппликатой точки М.

При заданной системе координат каждой точке М соответствует единственная упорядоченная тройка чисел (x, y, z) – её прямоугольные координаты и, наоборот, каждой упорядоченной тройке чисел (x, y, z) соответствует, и при том одна, точка М в пространстве.

Плоскости Oxy,Oxz,Oyz называются координатными плоскостями.

Скалярные и векторные

Величины

Некоторые величины в физике, механике и других науках полностью определяются заданием одного числа. Например, объем, масса, температура и др. Такие величины называются скалярными, а числа иногда называют скалярами. Но есть величины, для определения которых надо задать не только число, но и направление. Например, при изучении движения тела мы должны указать не только величину скорости, с которой движется тело, но и направление движения. При определении действия силы необходимо указать не только величину этой силы, но и направление её действия.

Такие величины называются векторными. Для работы с ними было введено понятие вектора, имеющее и самостоятельное значение в математике.

Любая упорядоченная пара точек А и B в пространстве определяет направленный отрезок, т.е. отрезок вместе с заданным на нём направлением. Если точка А – первая, то её называют началом отрезка, а точку B – его концом. Направлением отрезка считается направление от начала к концу отрезка.

Определение. Вектором называется направленный отрезок, или (что то же самое) упорядоченная пара точек.

Вектор обозначается 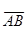- двумя буквами, при этом первая буква- начало вектора, а вторая - его конец.

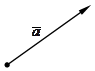
Вектор можно обозначать одной буквой с черточкой наверху - 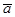. Направление вектора на рисунке указывается стрелкой.

Вектор, у которого начало и конец совпадают, называется нулевым и обозначается .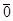

Расстояние между началом и концом вектора называется его длиной (или модулем)и обозначается 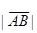или .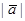

Векторы 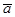и 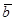называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Нулевой вектор считается коллинеарным любому вектору, так как он не имеет определенного направления, длина его, очевидно, равна нулю, т.е. .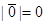

Определение. Векторы 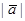и 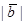называются равными 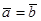, если они:

а) коллинеарны;

б) одинаково направлены;

в) равны по длине.

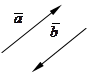
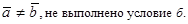
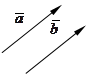
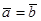
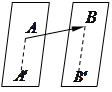
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, т.е. начало вектора может быть в любой точке пространства, но длина и направление фиксированы. Такие векторы называются свободными. В дальнейшем будем изучать только свободные векторы, называя их просто векторами.

Проекция вектора на ось

Рассмотрим некоторый вектор 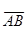и числовую ось Ou. Проведём через точки A и B плоскости, перпендикулярные к оси Ou. Обозначим через 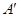и 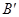точки пересечения этих плоскостей с осью.

Проекция вектора AB на ось Ou обозначается пр_uAB.

Определение. Проекцией вектора AB на ось Ou называется число, равное 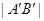, если направление 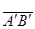совпадает с направлением Ou и 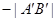, если направление 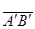противоположно Ou.

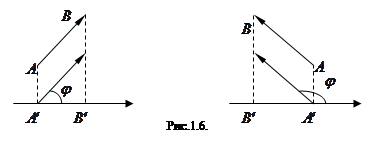
Нетрудно показать, что

пр_uAB= ,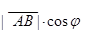

где j - угол, образованный вектором AB с осью Ou .

Координаты вектора. Пусть в пространстве задана прямоугольная система координат и произвольный вектор 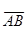. Пусть далее

.

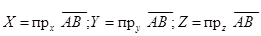Проекции X, Y, Z вектора 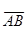называют его координатами и записывают так: .

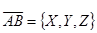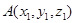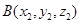Для любых точек и координаты вектора 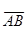определяются формулами

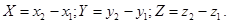
В этом случае модуль вектора 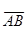находится по формуле

.

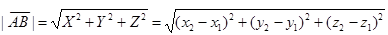Если через 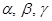обозначить углы наклона вектора к осям координат, то

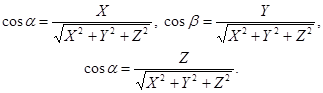
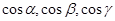называют направляющими косинусами вектора .

Очевидно, что .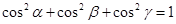

Пример.

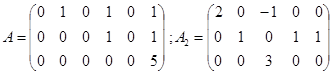
Определение. Элементарными преобразованиями матрицы называются следующие преобразования её строки:

а) перестановка двух каких-нибудь строк;

б) умножение элементов какой-либо строки на число, отличное от нуля;

в) прибавление к элементам какой-либо строки соответствующих элементов другой строки, умноженных на некоторое число.

Пример.

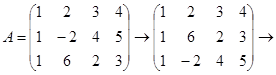
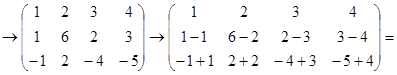
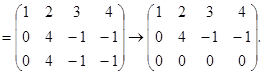
Из последней матрицы (ступенчатый вид) видно, что .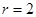

Приведем несколько утверждений без доказательств.

Теорема 1. При элементарных преобразованиях и отбрасывании нулевой строки ранг матрицы не изменяется.

Теорема 2. Всякую ненулевую матрицу можно привести к ступенчатому виду с помощью элементарных преобразований и выбрасывания нулевых строк.

Теорема 3. Ранг ненулевой матрицы равен числу строк её ступенчатого вида.

Рассмотрим систему:

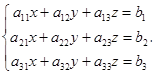
Определение. Матрица, составленная из коэффициентов при неизвестных системы, называется матрицей системы.

Определение. Матрица называется расширенной матрицей системы, если к матрице 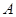присоединить столбец из свободных членов системы.

.

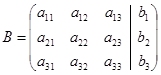Расширенная матрица- это закодированная запись системы. Строки матрицы соответствуют уравнениям системы. Умножение уравнения на число и сложение этого произведения с другим уравнением эквивалентно умножению строки матрицы на это число и почленному сложению произведения с другой строкой матрицы. Таким образом, работу с уравнениями мы можем заменить работой со строками матрицы.

Эффективным методом решения и исследования системы линейных уравнений является метод исключения неизвестных, называемый также методом Гаусса. Он состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему ступенчатого вида (или, в частности, треугольную систему), которая легко исследуется и решается. Применение метода Гаусса не зависит ни от числа уравнений, ни от числа неизвестных в системе.

Рассмотрим систему 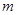линейных уравнений с 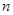неизвестными 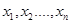,которую запишем в виде расширенной матрицы:

.

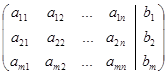Заметим, что иногда могут встречаться уравнения, все коэффициенты которых (т.е. соответствующая строка матрицы) равны 0:

.

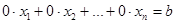Если в этом уравнении 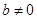, то ему, очевидно, не удовлетворяют никакие значения неизвестных, и система, содержащая хотя бы одно такое уравнение, несовместна, т.е. не имеет решения. Если же 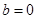, то ему удовлетворяют любые решения неизвестных, т.е. рассматриваемое уравнение является тождеством и его можно удалить из системы.

Элементарные преобразования матрицы, рассмотренные ранее, можно производить и над расширенной матрицей системы, поэтому в дальнейшем будем говорить об элементарных преобразованиях, не делая различий между уравнениями системы и строками расширенной матрицы.

Разберём идею метода Гаусса на конкретных примерах.

Пример 2.

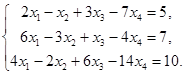
Решение.

I этап: запишем систему в виде расширенной матрицы

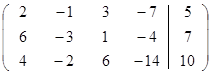
II этап: исключим с помощью первого уравнения x из остальных уравнений. Для этого домножим первую строку на –3 и сложим её со второй, затем умножим первую строку на –2 и сложим её с третьей.

Получим

.

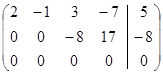Последняя строка состоит из нулей, если её расписать в виде уравнения, то получим

.

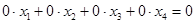Это уравнение является тождеством, поэтому его нет смысла оставлять в системе.

Раскодируем полученную матрицу:

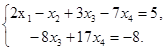
Выразим из второго уравнения :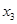

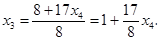
Подставим в первое уравнение вместо 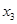его выражение через 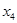и выразим :

,

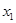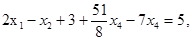
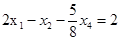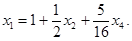
Ответ:

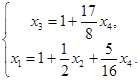
Получим так называемое общее решение системы, которое является формулой для получения конкретных её решений. Эти конкретные решения системы называются частными решениями. Получают их следующим образом: придавая переменным 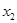, 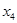произвольные значения и находя по этим значениям 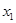и 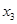, всякий раз находят решение системы. Так как 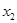и 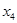можно придавать произвольные значения, то эти переменные называются свободными. Неизвестные 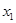и 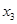, значения которых вычисляются по значениям 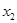и 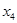, называются базисными.

Получим одно из частных решений в предыдущем примере. Пусть 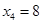, а 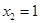, тогда , .

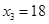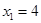Ответ: 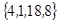-частное решение.

Пример 3.

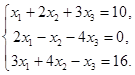
Решение.

Закодируем систему и приведем матрицу к треугольному виду

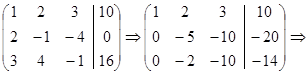
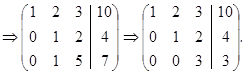
Таким образом, заданная система равносильна следующей:

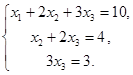
Находим 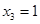из последнего уравнения, затем 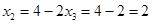из второго, и наконец, из первого:

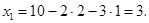
Ответ: .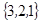

Пример 4.

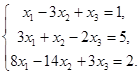
Выпишем расширенную матрицу и упростим её:

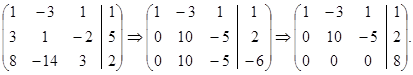
Полученная система

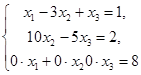
несовместна, так как её последнее уравнение не имеет смысла. Следовательно, исходная система также несовместна.

Построение обратной матрицы

Обратная матрица существует только для квадратной матрицы, определитель которой не равен нулю. Такая матрица называется невырожденной.

Пусть матрица 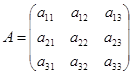- невырождена, т.е.

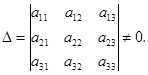
Построим союзную матрицу 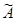, которая составлена из алгебраических дополнений элементов матрицы 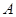, причём в столбцах матрицы 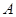записываются алгебраические дополнения соответствующих строк этой матрицы.

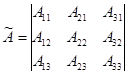, где

.

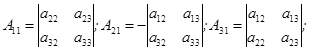
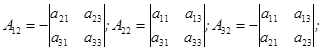
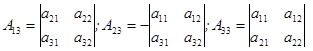Обратная матрица 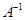имеет вид

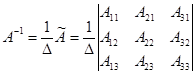
Решим систему (см. пример 1) матричным способом.

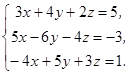
Здесь

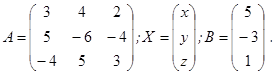
Решим матричное уравнение .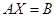

Составим обратную матрицу .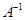

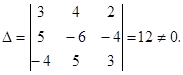
Выпишем все алгебраические дополнения для данной матрицы.

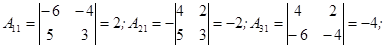
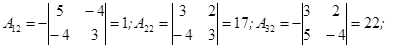
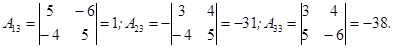
Составим матрицу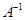

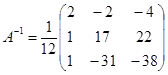
Решим матричное уравнение

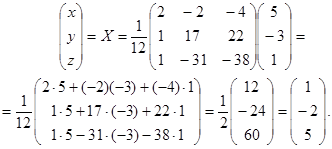
Отсюда получаем решение системы:

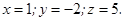
Ответ: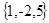

Замечание.

Аналогично, матричным способом, можно решать любые системы 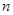уравнений с 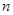неизвестными, если только определитель системы не равен нулю.

Контрольная работа №1 по теме

«Элементы линейной и векторной алгебры»

1.1. Вычислить определитель.

1.1.1.		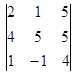1.1.2		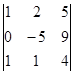1.1.3.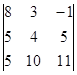
1.1.4.		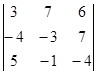1.1.5		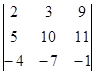1.1.6.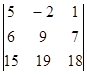
1.1.7.		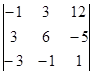1.1.8		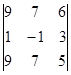1.1.9.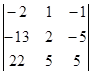
1.1.10.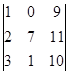

1.2. Решить систему трех уравнений с тремя неизвестными тремя способами: методом Гаусса, по формулам Крамера и матричным способом.

1.2.1.		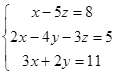1.2.2.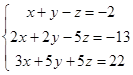
1.2.3.		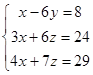1.2.4.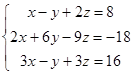
1.2.5.		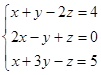1.2.6.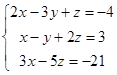
1.2.7.		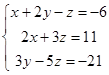1.2.8.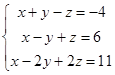
1.2.9.		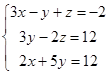1.2.10.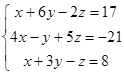

1.2. Вычислить .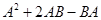

1.3.1.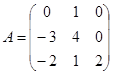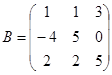
1.3.2.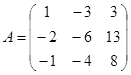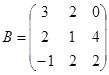
1.3.3.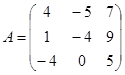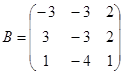
1.3.4.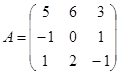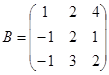
1.3.5.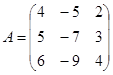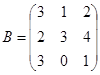
1.3.6.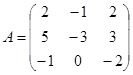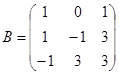
1.3.7.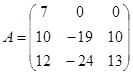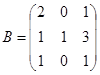
1.3.8.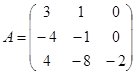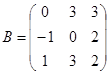
1.3.9.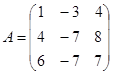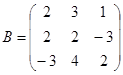
1.3.10.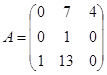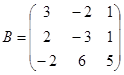

1.4. Даны векторы , , , .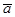

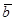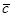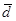1. Показать, что 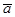, , 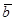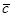образуют базис и найти координаты вектора 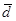в этом базисе.

2. Найти: a) ;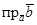

б) ;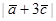

в) ;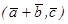

г) ;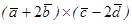

д) ;

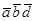е) угол между векторам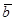и и .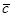

1.4.1.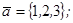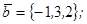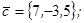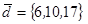
1.4.2.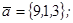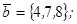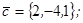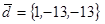
1.4.3.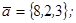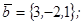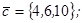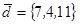
1.4.4.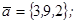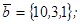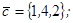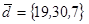
1.4.5.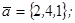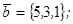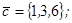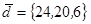
1.4.6.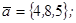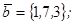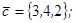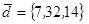
1.4.7.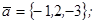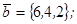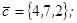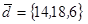
1.4.8.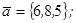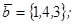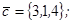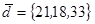
1.4.9.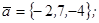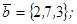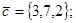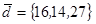
1.4.10.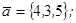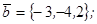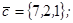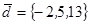

1.5. Даны точки , , ,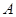

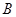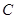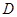
1. Показать, что точки 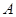, , 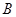, 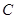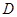не лежат в одной плоскости.

2. Вычислить: а)объем пирамиды ;

б)длину ребра ;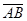

в) площадь грани ;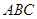

г)угол между граням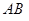и и .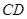

1.5.1.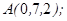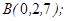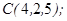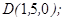
1.5.2.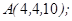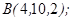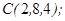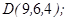
1.5.3.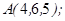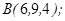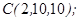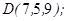
1.5.4.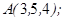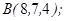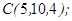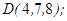
1.5.5.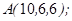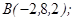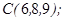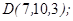
1.5.6.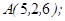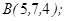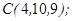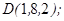
1.5.7.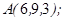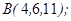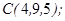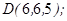
1.5.8.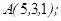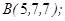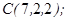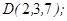
1.5.9.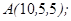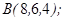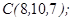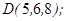
1.5.10.		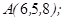Наши рекомендации Линейные операции над векторами Линейные операции над векторами Линейные операции над векторами Линейные операции над векторами Линейные операции над векторами Линейные операции над векторами Линейные операции над векторами. Линейные операции над векторами» Линейные операции с векторами. Линейные операции над векторами ← Предыдущая страница | Следующая страница →