Тема: Численное интегрирование в теплотехнических расчетах. Методы численного интегрирования.

План: Численное интегрирование при расчете площади поверхности нагрева теплообменного аппарата. Методы численного интегрирования: прямоугольника, трапеций, парабол, Гаусса. Компьютерная реализация теплового расчета теплообменного аппарата.

Численное интегрирование в теплотехнических расчетах

Необходимость численного интегрирования часто возникает при анализе инженерных и научных данных. Например, численные методы вычисления применяют в тех случаях, когда интеграл не удается найти в аналитическом виде или когда этот вид сложен. Численное интегрирование применяют и тогда, когда нужно найти интеграл от табулированной функции, измеряемой в эксперименте.

Например, для определения количества теплоты, передаваемого от одного теплоносителя к другому через поверхность теплообмена, необходимо воспользоваться уравнением теплопередачи вида

dQ = k<Dt>dF (4.1)

Из уравнения (4.1) t_x2

F=òdQ ¤ k<Dt> = òG_хc_рхdt_х ¤ k<Dt>(t_x,t_г )

t_x1

т.е задача сводится к взятию интеграла, что не всегда можно сделать аналитически.

Задача численного интегрирования состоит в нахождении приближенного значения интеграла вида:

,

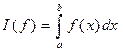где f(x) – заданная функция.

На отрезке [а,b] вводится сетка

ω ={x_i;; x₀ = а<x₁<x₂…<x_n = b}.

В качестве приближенного значения интеграла рассматривают число

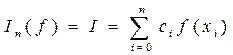, (4.2)

где f(x_i) – значения функции в узлах сетки;

с_i – весовые или квадратурные множители (веса), которые зависят только от узлов и не зависят от вида функции.

Формула (4.2) - квадратурная формула. Задача численного интегрирования будет состоять в отыскании таких узлов {x_i;} и таких весов {с_i;}, чтобы погрешность квадратурной формулы была минимальна для функций из заданного класса

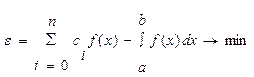
В зависимости от разбиения отрезка [а,b] различают два подхода к построению квадратурных формул. В первом - местоположение и длина интервалов разбиения выбираются заранее. В этом случае используется квадратурная формула Ньютона - Котеса (к этим методам относятся метод трапеции и метод Симпсона). Во втором - местоположение и длина интервалов заранее не задается, а подбирается так, чтобы достичь наивысшей точности при заданном числе интервалов (метод Гаусса).

Определенный интеграл

_b

I=ò f(x)dx (4.2)

^a

представляет собой площадь, ограниченную кривой f(x),осью х и прямыми х₀ = a, х _n= b. Мы будем пытаться вычислить интеграл, разбивая интервал от a до b на множество меньших интервалов, находя приблизительную площадь каждой полоски.

y f (x_i) f (x_i+1)

y = f (x)

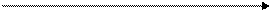
a x_i x_i+1 b x

Рисунок 4.1 – Геометрическая интерпретация численного интегрирования

Методы численного интегрирования

Формула прямоугольников

Впишем в каждую полоску прямоугольник. Для нахождения площади такого прямоугольника найдем координату средней точки х_ср = (x_i+x_i+1)/2 и значение функции в ней f (x_ср). Площадь под кривой определяется так

I=ΣI_i= Σf((x_i+x_i+1 )/2)*( x_i+1- x_i) (4.3).

Формула (4.3) - формула прямоугольников.

Оценим погрешность метода прямоугольников, для чего разложим функцию в ряд Тейлора и отбросим соответствующие члены ряда, содержащие h в степени больше 3.

Эта погрешность может быть определена так:

e_i = - (h³/24)* f ′′ (x_i),

ε = ∑ e_i = - (h²/24)* (b-a ) * f ′′ ( ξ ), (4.4).

где ξ є [ a , b ].

Метод трапеций

Впишем в каждую полоску трапецию. Площадь под кривой определяется так

I=ΣI_i= Σ1/2 (f (x_i+1)- f((x_i)) *( x_i+1- x_i) + f(x_i) *( x_i+1- x_i)

Формула трапеций на равномерной сетке шагом h =(x_i+1- x_i):

I = ∑ с_i * f (x_i) = h/2*( y₀ + 2y₁ + 2y₂ +... + y_n ) (4.5).

ⁱ

h = (b -а)/ n; у₀ = f (x₀); у₁ = f (x₁) и т.д.

Оценим погрешность метода трапеций, для чего разложим функцию в ряд Тейлора и отбросим соответствующие члены ряда, содержащие h в степени больше 3. Эта погрешность может быть определена так:

e_i = - (h³/12)* f ′′ (x_i)

ε = ∑ e_i = - (h²/12)* (b-a ) * f ′′ ( ξ ), где ξ є [ a , b ] (4.6).

4.2.3 Метод Симпсона

Этот метод аналогичен правилу трапеций в той части, где интегрирование производится путём разбиения общего интервала на множество более мелких отрезков. Однако теперь для вычисления площади каждой полоски через каждые три последовательные ординаты разбиения проводят квадратичную параболу.

Предположим, что число отрезков чётное:

n = (b-a) / h.

Воспользуемся методом трапеции:

I _h= h/2*( y₀ + 2y₁ + 2y₂ +... + y_n ) (4.7)

Площадь под кривой I = I _h+с h² (4.8)

Увеличим шаг в два раза k = 2h:

I _k= k/2*( y₀ + 2y₂ + 2y₄ +... + y_n ) (4.9)

Площадь под кривой I = I_k+с k². (4.10)

Исключив из системы уравнений (4.8) и (4.10) с, получим формулу Ричардсона для лучшего приближения интеграла

I = I _h+ (I _h - I_k)/ (k²/ h²-1) (4.11)

Подставим (4.7) и (4.9) в (4.11) получаем формулу Симпсона

I = h/3*( y₀ + 4y₁ + 2y₂ + 4y₃ + 2y₄ +... + y_n ) (4.12)

Ошибка ограничения, допускаемая в методе Симпсона

e_i = - (h⁴/180)* f ^(IV) (x_i)

ε = ∑ e_i = - (h⁴/180)* (b-a ) * f ^(IV) ( ξ ), (4.13)

где ξ є [a, b].

Метод трапеций и Симпсона наиболее часто используется при численном интегрировании.

Оценка погрешности ограничения рассмотренных методов численного интегрирования по выражениям (4.4), (4.6) и (4.13) оказываются малоэффективными из-за трудностей оценки производных высокого порядка подынтегральных функций. На практике для достижения требуемой точности прибегают к методу последовательного удвоения числа шагов. Задают значение допустимой погрешности ε и число интервалов разбиения n (шаг интегрирования h) находят I_n. Удваивают число интервалов (шаг интегрирования h/2) и находят I _2n. Оценивают погрешность Δ=( I_n- I _2n)/3 – для метода трапеций и Δ=( I_n- I _2n)/15 – для метода Симпсона. Если Δ≥ ε, количество интервалов еще раз удваивают. Вычисления заканчивают при выполнении условия Δ< ε.

4.2.4 Метод Гаусса

Гауссом предложен метод, позволяющий уменьшить ошибку ограничения при заданном числе интервалов за счет расположения концов интервалов там, где это требуется из условий достижения наивысшей точности интегрирования.

В заданном интеграле _b

I=ò f(x)dx,

^a

изменим пределы интегрирования так, чтобы они стали равны +1и –1, для чего введем новую переменную μ = (2х- (b+a))/(b-a)

₁

I=ò φ (μ)dμ, где φ (μ)=(1/2)(b-a) f((b-a) μ /2+(b+a)/2).

^-1

Можно показать, что

₁

I=ò φ (μ)dμ = φ (-1/√3) + φ (1/√3) +ε, (4.14)

^-1

где ε= φ ^(IV)/135.

(4.14)– формула Гаусса для двух ординат.

Можно вывести Гауссовы формулы численного интегрирования более высокого порядка с использованием полиномов Лежандра [1]. На практике предпочтение отдается методу Симпсона.

Интегрирование по квадратурным формулам сопровождается ошибками округления. Они носят случайный характер и с увеличением числа интервалов разбиения n возрастают пропорционально √n. Для функций высокой гладкости формула Гаусса дает значительно более точные результаты, чем формула Симпсона при одинаковом числе узлов, а последняя более точные, чем формула трапеций. Формула Гаусса обеспечивает высокую точность при небольшом числе узлов. Формула Симпсона в достаточной степени точна при умеренном числе узлов и поэтому получила широкое применение. Компьютерная реализация методов интегрирования описана в [9], [23-26].

Литература: [1-4],[6],[22-24].

Лекция 5