Динамические эконометрические модели

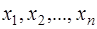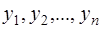Теперь рассмотрим модели временных рядов, где в качестве исходных статистических данных мы располагаем наблюдениями двух временных рядов и . Целью регрессионного анализа в данном случае является построение линейной регрессионной модели, позволяющей с наименьшими ошибками прогнозировать значения y_t по значениям x_t для t>n.

Подобные модели естественны в ситуациях, когда две переменные x и y связаны так, что воздействия единовременного изменения одной из них (x) на другую (y) сказывается в течение достаточно продолжительного времени, т.е. наблюдается распределенный во времени эффект воздействия. В частности, такие связи возникают между регистрируемыми во времени входными и выходными характеристиками процессов накопления и распределения ресурсов (например, процессов преобразования доходов населения в его расходы) или процессов трансформации затрат в результаты (например, процессов воспроизводства основных доходов).

Эконометрическая модель является динамической, если в данный момент t она учитывает значения входящих в неё переменных, относящихся как к текущему, так и к предыдущим моментам времени, т.е. модель учитывает, отражает динамику исследуемых переменных в каждый момент времени.

Переменные, влияние которых характеризуется определенным запаздыванием, называются лаговыми переменными.

Классифицируются динамические модели по – разному. Один из вариантов классификации следующий:

1. Модели с распределенными лагами. Они содержат в качестве лаговых переменных лишь независимые (объясняющие) переменные, например:

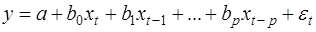(15)

2. Авторегрессионные модели, уравнения которых включают в качестве объясняющих переменных лаговые значения зависимых переменных, например:

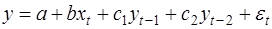(16)

Рассмотрим модель (15), приняв, что р – конечное число. Модель говорит о том, что если в некоторый момент времени t происходит изменение х, это изменение будет влиять назначение у в течение р последующих моментов времени. Коэффициент b₀ называется краткосрочным мультипликатором, т.к. он характеризует изменение среднего значения у при единичном изменении х в тот же самый момент времени. Сумма 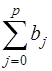называется долгосрочным мультипликатором; он характеризует изменение у под воздействием единичного изменения х в каждом из моментов времени. Любая сумма 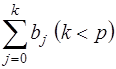называется промежуточным мультипликатором.

Относительные коэффициенты модели (15) с распределенным лагом определяются выражениями:

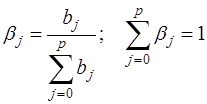(17)

(условие нормировки имеет место, только если все b_j имеют одинаковые знаки). Значения β_j являются весами для соответствующих коэффициентов b_j. Каждый из них измеряет долю общего изменения у, приходящегося на момент (t+j).

Средний лаг определяется по формуле средней арифметической взвешенной:

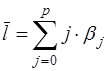(18)

Он означает период, в течение которого происходит изменение результата от изменения х в момент t. Небольшая величина (18) означает быструю реакцию у на изменение х, высокое значение говорит о том, что воздействие фактора у будет сказываться в течение длительного времени.

Медианный лаг – это величина лага, для которого

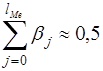(19)

Это время, в течение которого с момента t будет реализована половина общего воздействия фактора на результат.

Рассмотрим условный пример. Предположим, модель зависимости объёмов продаж компании от расходов на рекламу имеет вид:

.

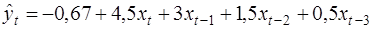Краткосрочный мультипликатор равен 4,5: увеличение расходов на рекламу на 1 млн. руб. приводит к среднему росту продаж компании на 4,5 млн. руб. в том же периоде.

В момент (t+1) такой рост составит 4,5+3,0=7,5 млн. руб., в момент (t+2) - 7,5+1,5=9 млн. руб. и т.д. долгосрочный мультипликатор равен 9,5. В долгосрочной перспективе (в течение 3 месяцев) увеличение расходов на 1 млн. руб. приведет к общему росту продаж на 9,5 млн. руб.

Относительные коэффициенты:

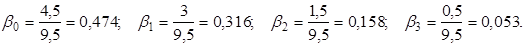
47,4% общего увеличения объёма продаж от роста затрат на рекламу происходит в текущем месяце, 31,6% - в следующем месяце и т.д.

Средний лаг равен:

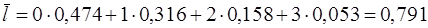(мес.)

- небольшая величина, поскольку большая часть эффекта роста затрат на рекламу проявляется сразу же. Медианный лаг в данном примере составляет чуть более 1 месяца.

Модель (15) можно свести к уравнению множественной регрессии через замены переменных:

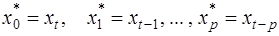, (20)

в результате получаем:

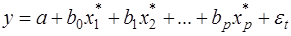(21)

Однако применение обычного МНК затруднительно по следующим причинам:

1. Текущие и лаговые значения х тесно связаны между собой, что приводит к высокой мультиколлинеарности факторов.

2. При большой величине лага велико число параметров, что приводит к уменьшению числа степеней свободы.

3. Часто возникает проблема автокорреляции остатков.

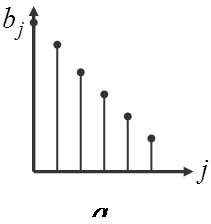
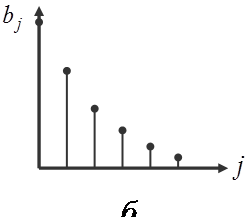
Поэтому оценки параметров становятся неточными и неэффективными. Для получения более обоснованных оценок нужна информация о структуре лага. Эта структура может быть различной. На рисунке представлены некоторые её формы:

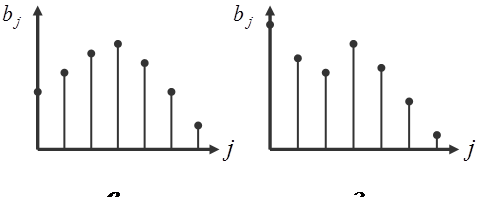Если с ростом величины лага коэффициенты при лаговых переменных убывают, то имеет место линейная (или треугольная) структура лага (а), а также геометрическая структура (б). Возможны и другие структуры лага (в или г). Рассмотрим некоторые подходы к расчету лагов.

Лаги Алмон. Предполагается, что в модели (15) с конечной максимальной величиной лага р значения коэффициентов b_j описываются полиномом к – й степени:

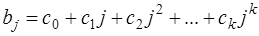(22)

Каждый коэффициент, таким образом, запишется так:

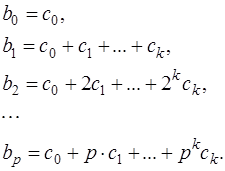(23)

Подставим эти соотношения в (15) и перегруппируем слагаемые, получим:

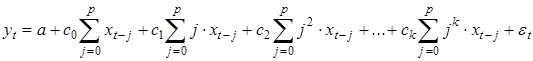24)

Обозначим суммы соответственно как новые переменные 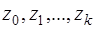, перепишем (24) в виде:

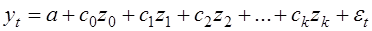(25)

Параметры с_j определяются по МНК.

Достоинства метода:

1. Универсальность, применимость для моделирования процессов с разнообразными структурами лагов.

2. При малых k (2 или 3) можно построить модели с распределенным лагом любой длины.

Ограничения метода:

1. Величина р должна быть известна заранее. При этом приходится задавать максимально возможную величину лага. Выбор меньшего лага, чем его реальное значение, приведет к неверной спецификации модели, невозможности обеспечить случайность остатков, поскольку влияние значимых факторов будет выражено в остатках. Оценки параметров при этом окажутся неэффективными и смещенными. Включение в модель большей величины лага, чем его реальное значение, снижает эффективность оценок из – за наличия статистически незначимых факторов.

2. Необходимость установить степень полинома. Обычно принимают k=2 или 3 по правилу: степень полинома k должна быть на единицу больше числа экстремумов в структуре лага. В крайнем случае k определяется из сравнения моделей для различных k.

3. Возможна мультиколлинеарность факторов z_j, однако она сказывается здесь в меньшей степени, чем в модели (15).

Метод Койка. Этот метод применяется в модели с бесконечным лагом:

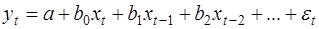(26)

Здесь обычный МНК применить нельзя. Для идентификации модели (26) предполагается, что параметры с увеличением лага убывают в геометрической прогрессии, т.е. с постоянным темпом :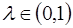

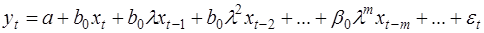(27)

Запишем выражение (27) для момента (t-1):

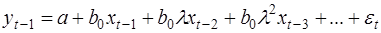(28)

Умножим (28) на λ и вычтем из (27):

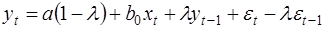
или

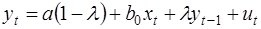(29)

Это модель авторегрессии. Определив её параметры, находим λ, а, b₀ исходной модели, а затем и параметры 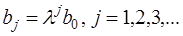. Данная модель позволяет определить долгосрочный мультипликатор 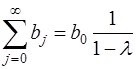и средний лаг .

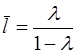Теперь перейдем к рассмотрению авторегрессионных моделей.

Модель адаптивных ожиданий. Моделирование ожиданий является сложной задачей, поскольку фактор ожидания имеет качественную специфику. Например, инвестиции связаны не только с нормой процента, но и с ожиданиями инвесторов. Если в стране существенная безработица, то действия правительства в направлении стимулирования могут рассматриваться как позитивные, и это способствует инвестициям. Если экономика близка к полной занятости, то та же самая политика будет рассматриваться как ведущая к росту инфляции и приведет к падению инвестиционной активности.

Модель адаптивных ожиданий заключается в простой процедуре корректировки ожиданий, когда в каждый момент времени реальное значение переменной сравнивается с её ожидаемым значением. Если реальное значение оказывается больше, то ожидаемое в следующий момент значение корректируется в сторону его увеличения, если меньше – то в сторону уменьшения. Предполагается, что размер корректировки пропорционален разности между реальным и ожидаемым значениями переменной. Таким образом, основную идею можно записать формулой:

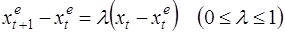(30)

где 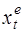- значение х, ожидаемое в момент t (expected). Это выражение можно переписать в форме взвешенного среднего:

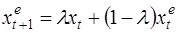(31)

Модель (30) и является моделью адаптивных ожиданий. Это выражение иногда называют моделью обучения на ошибках, т.к. ожидания экономических объектов складываются из прошлых ожиданий, поправленных на величину ошибки в ожиданиях, допущенных ранее.

При λ=0 ожидания являются статичными, неизменными, т.е. .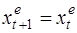

При λ=1 ожидания реализуются мгновенно, т.е. .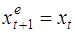

Чем больше λ, тем быстрее ожидаемое значение адаптируется к предыдущим реальным значениям переменной.

Долгосрочная функция модели адаптивных ожиданий записывается в виде:

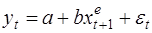(32)

Подставим сюда выражение (31), получим:

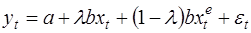(33)

Запишем его для (t-1):

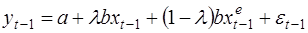(34)

Умножим (34) на (1-λ) и вычтем почленно из (32):

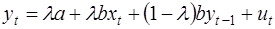, (35)

где .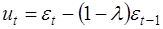

Это модель авторегрессии, в которой все переменные имеют фактические, а не ожидаемые значения. Модель в форме (35) называется краткосрочной функцией модели адаптивных ожиданий.

Модель неполной (частичной) корректировки. Здесь поведенческое уравнение определяет не фактическое значение y_t, а её желаемый (целевой) уровень :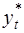

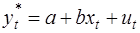(36)

Примером такой модели служит политика компаний относительно распределения дивидендов: прибыль расходуется частично на уплату дивидендов, частью на инвестиции. Когда прибыль увеличивается, дивиденды тоже растут, но не в той же пропорции (это объясняется желанием руководства фирмы в любом случае не уменьшать дивиденды, т.к. это ударяет по репутации фирмы).

В модели предполагается, что фактическое приращение зависимой переменной пропорционально разнице между её желаемым уровнем и значением в предыдущий период:

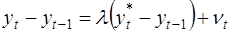(37)

(ν_t – случайный член). Это выражение можно переписать так:

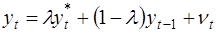, (38)

т.е. в форме взвешенного среднего. Чем больше λ, тем быстрее идет корректировка. При λ =1 полная корректировка происходит за один период. При λ =0 корректировка не происходит совсем.

Подставим (36) в (38), получим:

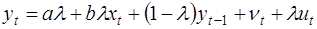(39)

Это и есть модель частичной корректировки, которая также является моделью авторегрессии.

Несколько слов об оценке параметров уравнений авторегрессии. Рассмотрим уравнение:

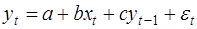(40)

Во всех рассмотренных выше моделях стоит проблема оценивания параметров. Обычный МНК чаще всего даёт смещенные и несостоятельные оценки, вследствие автокорреляции между случайными отклонениями ε_t и ε_t-1 и корреляции между y_t-1 и ε_t.

Один из возможных методов расчета параметров – метод инструментальных переменных, состоящий в замене y_t-1 на новую переменную, которая тесно коррелирует с y_t-1, но не коррелирует с остатками. Это можно сделать двумя способами.

1. Провести регрессию

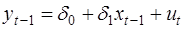, (41)

или

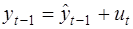
и подставить 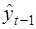в уравнение авторегрессии, получаем:

, (42)

и далее применяем обычный МНК.

2. Подставим (41) в (40), получим модель с распределенным лагом:

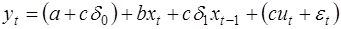, (43)

для которой не нарушаются предпосылки обычного МНК.