Соединение “звездой” с нулевым проводом
а) Определяем полное сопротивление каждой фазы нагрузки, например фазы «а»:
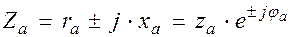, где 
.
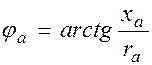б) Записываем фазные напряжения генератора:
; 
; 
,
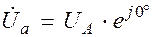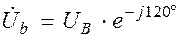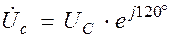где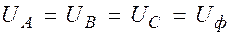 
.
в) Принимая соединительные провода идеальными, записываем фазные напряжения нагрузки:
; 
; 
.
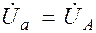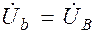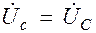г) В комплексной форме рассчитываем токи в фазах, например фазы «а»: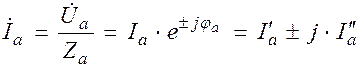 
,
где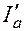 
и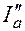 
– активная и реактивная составляющие тока.
д) Рассчитываем потребляемую полную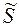 
, активную P и реактивную Q мощности нагрузки:
,
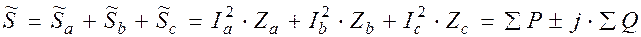где сумма вещественных частей дает значение активной мощности P, а мнимых – реактивной Q.
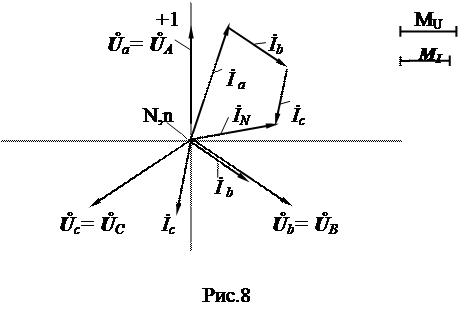
е) Строим векторную диаграмму напряжений и токов на комплексной плоскости. Для удобства построений плоскость разворачиваем на 90° против часовой стрелки. Построение векторов удобно вести по их проекциям, используя алгебраическую форму записи. Геометрическая сумма фазных токов должна дать ток нейтрали. Пример построения диаграммы приведен на рис. 8.
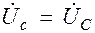
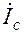
Соединение “звездой” без нулевого провода
а) Определяем напряжение смещения нейтрали:
,
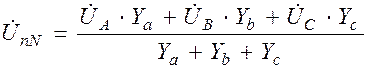где Ya,Yb,Yc – комплексы полной проводимости фаз, например, фазы «а»:
;
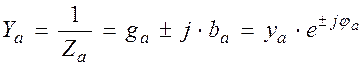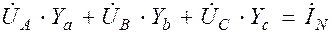– ток в нейтральном проводе берется из предыдущего расчёта.
б) Определяем напряжения на фазах нагрузки:
; 
; 
. 
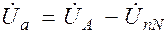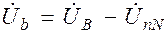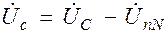в) Определяем токи в фазах нагрузки:
; 
; 
.
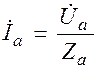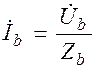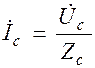г) Делаем проверку: İa + İb + İc = 0.
д) Рассчитываем полную, активную и реактивную мощности, потребляемые нагрузкой. Расчёт ведётся аналогично предыдущему.
е) Строим векторную диаграмму напряжений и токов.
Сначала строим векторы фазных напряжений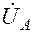 
, 
, 
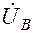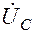генератора, затем – 
, 
, 
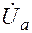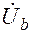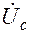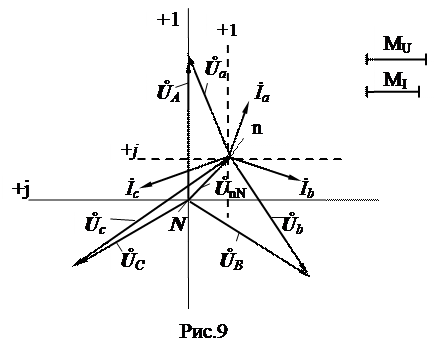
нагрузки, для чего строится вектор напряжения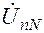 
смещения нейтрали. Векторы фазных токов İa ,İb ,İc нагрузки строим относительно точки n смещения нейтрали, например, как на рис. 9. Геометрическая сумма фазных токов должна равняться нулю.
3. Соединение “треугольником”
а) Находим линейные напряжения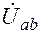 
, 
, 
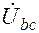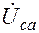с учётом опережения соответствующих фазных напряжений на угол 30°, например:
.
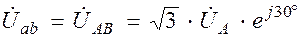б) Определяем токи в фазах нагрузки:
; 
; 
,
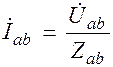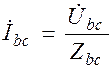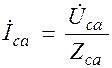где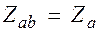 
; 
; 
.
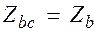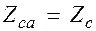в) Рассчитываем линейные токи:
; 
; 
.
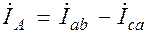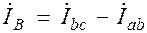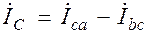г) Делаем проверку: İA + İB + İC = 0.
д) Рассчитываем полную, активную и реактивную мощности. Расчет ведется аналогично предыдущему.
е) Строим векторную диаграмму напряжений и токов. На системе векторов фазных напряжений 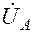, , 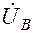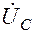строим систему линейных напряжений 
, 
, 
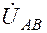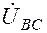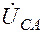. В начале векторов линейных напряжений располагаем вспомогательные оси. Начала векторов фазных токовİab,
İbс, İcaрасполагаем в начале одноименных векторов напряжений. Векторы линейных токов строим на основе ранее записанных уравнений.
Пример построения векторной диаграммы показан на рис. 10, где вспомогательные оси обозначены пунктирной линией.
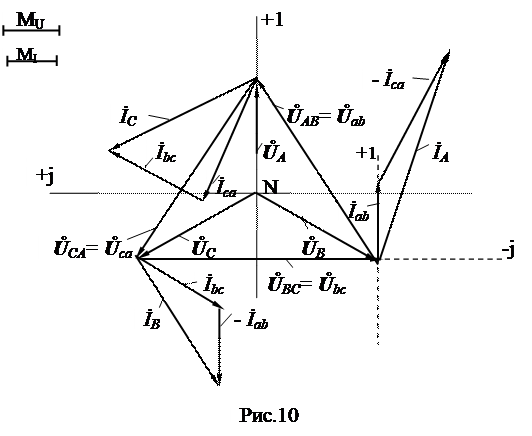
Рис. 10
ПРИЛОЖЕНИЕ 1
Исходные данные для расчёта цепей постоянного тока
Таблица 1
| Ц и ф р ы в а р и а н т а з а д а н и я | ||||||||||||
| первая | вторая | третья | ||||||||||
| № | № схемы | № | NK | E1 | E2 | № | R1 | R2 | R3 | R4 | R5 | R6 |
| - | - | - | В | - | Ом | |||||||
Схемы к табл. 1
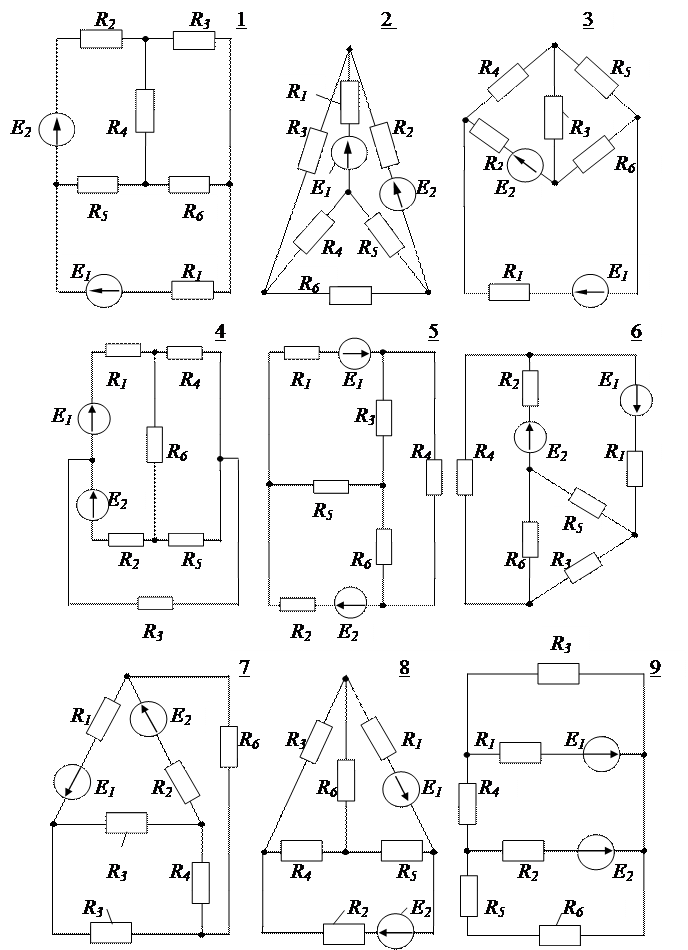
ПРИЛОЖЕНИЕ 2
Исходные данные для расчёта однофазных цепей
Переменного тока
Таблица 2
| Ц и ф р ы в а р и а н т а з а д а н и я | ||||||||||||||
| первая | вторая | третья | ||||||||||||
| № | № схемы | U | ¦ | № | r1 | r2 | r3 | № | C1 | C2 | C3 | L1 | L2 | L3 |
| - | В | Гц | - | Ом | - | мкФ | мГн | |||||||
| 6,35 | 9,55 | 15,9 | ||||||||||||
| 15,9 | 25,5 | 15,9 | ||||||||||||
| 6,35 | 15,9 | 9,55 | ||||||||||||
| 6,35 | 9,55 | 6,35 | ||||||||||||
| 9,55 | 15,9 | 12,75 | ||||||||||||
| 25,5 | 15,9 | 6,35 | ||||||||||||
| 31,8 | 15,9 | 6,35 | ||||||||||||
| 19,1 | 9,55 | 12,75 | ||||||||||||
| 12,75 | 25,5 | 19,1 |
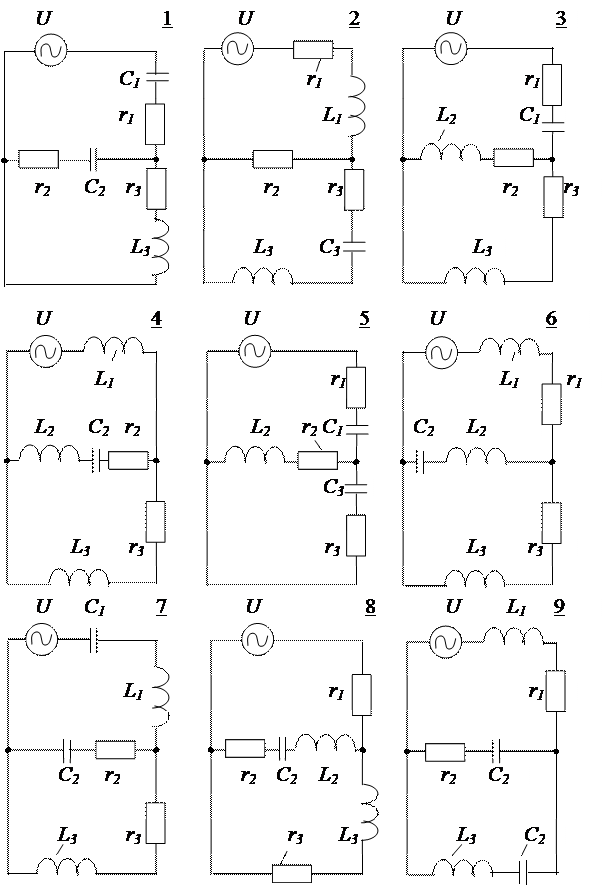
Cхемы к табл. 2
 |
ПРИЛОЖЕНИЕ 3
Исходные данные для расчёта трёхфазных цепей
Таблица 3
| Ц и ф р ы в а р и а н т а з а д а н и я | |||||||||
| первая | вторая | третья | |||||||
| № | Uф | № | ra=rab | rb=rbc | rc=rca | № | jxa=jxab | jxb=jxbc | jxc=jxac |
| - | В | - | Ом | - | Ом | ||||
| -4 | |||||||||
| -3 | |||||||||
| -24 | |||||||||
| -10 | -6 | ||||||||
| -24 | |||||||||
| -12 | |||||||||
| -12 | |||||||||
| -20 | -8 | ||||||||
| -24 | -9 |
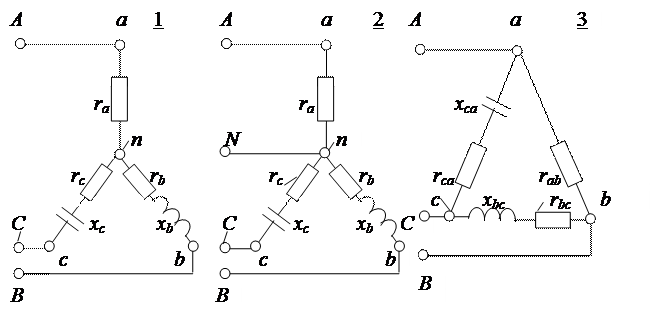
Схемы к табл. 3, например, вариант № 275
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Касаткин А.С. Электротехника / А.С. Касаткин, М.Б. Немцов. – М.: Энергоатомиздат, 1983. – 440 с.
2. Электротехника / Под ред. В.Г. Герасимова. – М.: Высш. шк., 1985. – 480 с.
3. Борисов Ю.М. Электротехника / Ю.М. Борисов, Д.Н. Липатов, Ю.Н. Зорин. – М.: Энергоатомиздат, 1985. – 547 c.
4. Сборник задач по электротехнике и основам электроники / Под ред. В.Г. Герасимова. – М.:Высш. шк., 1987. – 250 с.
СОДЕРЖАНИЕ
Введение . . . . . . . . . . . . . . . . . . . . 1
Задание № 1. Расчёт цепей постоянного тока . . . . . . . . 1
Задание № 2. Расчёт однофазных цепей переменного тока . . . 8
Задание № 3. Расчёт трёхфазных цепей . . . . . . . . . 14
Приложение 1 . . . . . . . . . . . . . . . . . . 19
Приложение 2 . . . . . . . . . . . . . . . . . . 21
Приложение 3 . . . . . . . . . . . . . . . . . . 23
Список рекомендуемой литературы . . . . . . . . . . . 24
Составитель
Владимир Евгеньевич Беспалов
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО
И ПЕРЕМЕННОГО ЭЛЕКТРИЧЕСКОГО ТОКА
Методические указания по выполнению заданий
курса “Электротехника и основы электроники”
для специальностей 150200, 090100, 090200, 090300, 090400, 090500, 170100
всех форм обучения
Редактор З.М. Савина
Подписано в печать 10.06.03. Формат 60´80/16. Бумага офсетная.
Отпечатано на ризографе.
Уч.-изд. л. 1,5. Тираж 150 экз. Заказ
ГУ КузГТУ, 650026, Кемерово, ул. Весенняя, 28.
Типография ГУ КузГТУ, 650099, Кемерово, ул. Д. Бедного, 4а.