Числовые характеристики случайных величин

Математическое ожидание. Мода и медиана. Пусть задана дискретная случайная величина Х, принимающая значения с вероятностями , …. Введем числовую характеристику положения значений случайной величины Х на оси абсцисс с учетом того, что эти значения имеют различные вероятности. Вычислим

или , так как .

Рассмотрим случай, когда ряд сходится.

Определение 2.7. Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех ее возможных значений и соответствующих им вероятностей:

. (2.8)

Выясним далее смысл математического ожидания как числовой характеристики.

Для этого рассмотрим дискретную случайную величину Х с рядом распределения

хi	х1	х2	х3	…	хn
pi	p1	p2	p3	…	pn

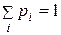
Пусть произведено N экспериментов, в результате которых значение х₁ появилось М₁ раз, х₂ – М₂ раз, ..., х_n – М_n раз. Найдём среднее арифметическое наблюдаемых значений случайной величины X:

.

Но есть не что иное, как частость наступления события , откуда

Согласно закону больших чисел (который будет изучен позже), частости наступления событий 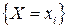сколь угодно мало отличаются от вероятностей р_i наступления этих событий при достаточно большом п и устойчивых условиях эксперимента с вероятностью, сколь угодно близкой к единице:

Поэтому при больших п с вероятностью сколь угодно близкой единице можно утверждать, что М(Х) , т.е.

.

Итак, выражение естественно считать числовой характеристикой, описывающей центр распределения. Отметим, что математическое ожидание – постоянное число, т.е. величина неслучайная, а среднее арифметическое может изменяться при дублировании эксперимента, т. е. является величиной случайной.

Распространим определение математического ожидания на непрерывные случайные величины.

Пусть непрерывная случайная величина Х задана плотностью вероятностей р(х) и все возможные значения Х принадлежат отрезку [а, b]. Разобъём этот отрезок на п отрезков длиной , и выберем в каждом из них произвольную точку . Составим далее сумму произведений значений и вероятностей попадания в заданный интервал , т. е. . Это интегральная сумма, поэтому ее предел при условии, что максимальная длина отрезка разбиения стремится к нулю равен определенному интегралу, т.е

.

Если возможные значения случайной величины Х принадлежат всей числовой оси, то получим несобственный интеграл

Определение 2.8. Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат всей числовой оси, называется несобственный интеграл

, (2.9)

где р(х) – плотность распределения вероятностей.

Кроме математического ожидания, которое является важнейшей характеристикой положения значений случайной величины на числовой оси, применяются и другие числовые характеристики, в частности мода и медиана случайной величины.

Определение 2.9. Модой дискретной случайной величины, обозначаемой Мо, называется ее наиболее вероятное значение, а модой непрерывной случайной величины – значение, при котором плотность вероятности максимальна.

На рис. 2.8 и 2.9 указаны значения моды для дискретных и непрерывных случайных величин.

Следует отметить, что распределения случайных величин могут иметь несколько значений моды (рис. 2.10).

Определение 2.10. Медианой случайной величины Х называется такое ее значение Ме, для которого одинаково вероятно, окажутся ли значения случайной величины меньше или больше Ме: Р(Х < Ме) = Р(Х > Ме), т. е. медиана – это корень уравнения .

С геометрической точки зрения медиана — это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам (рис. 2.11). В случае симметрического распределения медиана совпадает с модой и математическим ожиданием (рис. 2.12).

Рис. 1.10

Свойства математического ожидания. Сформулированные ниже свойства математического ожидания справедливы для дискретных и непрерывных случайных величин. Доказательство этих свойств, проведем для дискретных случайных величин.

Введем понятие системы дискретных случайных величин. Рассматривая совокупность случайных величин Х₁, Х₂, Х_3, .... Х_т, предполагают, что их значения определяются одним и тем же случайным экспериментом. Если – одно из возможных значений системы Х₁, Х₂, Х_3, .... Х_т, то событию соответствует определенная вероятность, удовлетворяющая аксиомам Колмогорова. Функция определенная при любых возможных значениях Х₁, Х₂, Х_3, .... Х_т случайных величин Х₁, Х₂, Х_3, .... Х_т называется совместным законом распределения.

Эта функция позволяет вычислять вероятности любых событий из 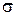- алгебры . В частности, совместный закон распределения случайных величин Х₁ и Х₂, которые принимают значения из множеств и , задается вероятностями. Будем рассматривать случайные величины Х₁Х₂…Х_т и Х₁+Х₂ +...+Х_т, возможные значения которых равны произведениям и суммам каждого возможного значения одной составляющей и каждых возможных значений других составляющих. Вероятности этих возможных значений равны произведениям соответствующих вероятностей.

Кроме того, будем использовать понятие независимости случайных величин, которое понимается так же, как и независимость событий. Строгое определение независимости случайных величин дано ниже.

1^о. Математическое ожидание постоянной величины равно самой постоянной, т.е. М(С) =С.

Действительно, постоянную С можно рассматриватькак дискретную случайную величину, принимающую значение С с вероятностью 1. Следовательно, .

2^о. Постоянный множитель можно выносить за знак математического ожидания: М(СХ) =СМ(Х) .

Доказательство. Пусть случайная величина Х задана законом распределения вероятностей:

хi	х1	х2	…	хn	…
pi	p1	p2	…	pn	…

Очевидно, что случайная величина СХ также является дискретной и принимает значения Сх₁, Сх₂ ,..., Сх_п, … с прежними вероятностями р₁, р₂, …, р_п, …, т.е. закон распределения СХ имеет вид

Схi	Сх1	Сх2	…	Схn	…
pi	p1	p2	…	pn	…

Тогда по определению математического ожидания и так как постоянный множитель можно выносить за знак суммы, то получаем утверждение свойства:

М(СХ) = Сх₁ р₁+Сх₂p₂+... + Сх_пр_п =С(х₁ р₁+ х₂p₂ +... + х_пр_п) = СМ(Х).

3^о. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий:

Доказательство. Рассмотрим случайную величину Х₁Х₂ и докажем вначале, что .

Действительно, если Х₁Х₂ заданы рядами распределения (табл. 2.1 и 2.2):

Таблица 2.1

(Х1)i	x1	x2	…
pi	p1	p2	…

Таблица 2.2

(Х2)j	x1*	x2*	…
pj*	p1*	p2*	…

то, как было указано выше, случайная величина Х₁Х₂ имеет следующий закон распределения:

(Х1Х2)i	x1x1*	x2x1*	x1x2*	x2x2*	…
pi	p1p1*	p2p1*	p1p2*	p2p2*	…

Тогда

Предположим далее, что это свойство выполняется для произведения случайной величины, т.е.

идокажем, что оно выполняется для произведения п случайных величин. Дпя этого введем обозначение .

Тогда по доказанному, а по предположению. Следовательно, , что и требовалось доказать.

4^о. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых:

Доказательство. Пусть заданы две случайные величины Х₁ и Х₂ рядами распределения (см. табл. 2.1 и 2.2).

В силу вышесказанного возможные значения случайной величины Х₁ + Х₂ будут . Их вероятности равны , так как они определяются по теореме умноже-ния вероятностей. Действительно, вероятность Р(х_i+х_j) обозначает вероятность того, что события и наступают совместно (одновременно),т.е.

Переходя к математическому ожиданию рассматриваемой суммы,имеем

Предположим далее, что свойство 4° справедливо для п–1 случайной величины:

Тогда, введя обозначение , получим, что

по доказанному, а по предположению. Следовательно,

Дисперсия случайной величины. На практике часто требуется оценить рассеивание возможных значений случайной величины вокруг ее среднего значения. На первый взгляд может показаться, что проще всего вычислить все возможные значения отклонения (разность между значением случайной величины и ее математическим ожиданием называется отклонением и обозначается Х–М(Х)) Х – М(Х) случайной величины и затем найти их среднее значение. Однако среднее арифметическое отклонений может быть равно нулю, хотя сами отклонения будут большими по модулю. Это объясняется тем, что значения могут иметь противоположные знаки и взаимно погашаться при нахождении среднего арифметического. Поэтому для характеристики рассеивания вычисляют дисперсию и среднее квадратическое отклонение.

Определение 2.11. Дисперсией случайной величины называется математическое ожидание квадрата ее отклонения:

D(Х) = М(Х- М(Х))².

Применив определение математического ожидания, получим формулы для вычисления дисперсии случайной величины Х:

(2.10)

Дисперсию случайной величины можно вычислять, применяя следующую теорему.

Теорема 2.5. Дисперсия случайной величины равна математическому ожиданию ее квадрата минус квадрат математического ожидания:

D(Х) = М(Х²) — (М(Х))² .

Доказательство. Действительно, из определения 2.11 с помощью тождественных преобразований, учитывая, что М(Х), –2М(Х), М²(Х) – постоянные величины, получим утверждение теоремы:

D(Х) = М(Х – М(Х))² =М(Х² - 2ХМ(Х) + (М(Х))²) =

= М(Х²) - 2(М(Х))² + (М(X)²) = М(Х²) - (М(X))² .

Тогда формулы (2.10) примут следующий вид:

(2.11)

Свойства дисперсии.Дисперсия спучайной величины удовлетворяет следующим свойствам.

1^о. Дисперсия постоянной величины С равна нулю: D(С)=0. Действительно, D(С) =М(С–М(С))² =М(С–С) = 0.

2^о. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(СХ) =С²D(Х).

Доказательство. По определению 2.11 и в силу свойств математического ожидання, получим:

D(CХ) =М(СХ–М(СХ))²=М(СХ–СМ(Х))²=М(С(Х–М(Х)))²=

=M(C²(Х–М(Х))²)=С²M(Х–M(X))²=C²D(X).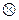

3^о. Дисперсия суммы нескольких независимых случайных величин равна сумме дисперсий этих величин:

Доказательство. Докажем вначале, что

По теореме 2.5 дисперсию суммы можно вычислить по формуле:

Предположим далее, что дисперсия суммы случайной величины равно сумме дисперсий

и докажем свойство 3^о для п случайных величин. Обозначим , тогда по доказанному, а по предположению. Следовательно,

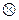
Следствие 1. Дисперсия суммы постоянной величины С и случайной величины равна дисперсии случайной величины Х: D(С+Х) = D(Х). Действительно, D(С+X) =D(С)+D(X) =0+D(X) =D(X).

Следствие 2. Дисперсия разности двух независимых случайных величин Х и Y равна сумме их дисперсий: D(Х – Y) = D(Х) + D(Y) .

Доказательство. Используя свойства 2° и 3° , получаем

D(X – Y) = D(X)+D(–Y) = D(X) + (–1)² D(Y) = D(X) +D(Y) .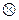

Дисперсия случайной величины как характеристика рассеивания имеет одну неприятную особенность: ее размерность, как видно из определения дисперсии, равна квадрату размерности случайной величины Х. Поэтому для характеристики отклонений случайной величины Х, имеющих размерность, одинаковую с размерностью случайной величины, вводится приведенное ниже определение.

Определение 2.12. Средним квадратическим отклонением (стандартом) случайной величины Х называется арифметический корень из дисперсии, т.е. .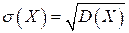

Таким образом, зная введенные две числовые характеристики – математическое ожидание М(Х) и среднее квадратическое отклонение , –получаем ориентировочное представление о пределах возможных значений случайной величины.

Моменты распределения случайных величин. Обобщением основных числовых характеристик случайных величин, описывающих центр распределения (математического ожидания, моды, медианы) и рассеивание (дисперсии и среднего квадратического отклонения), является понятие моментов случайных величин.

Определение 2.13. Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-й степени этой случайной величины, т.е., .

Из определения математического ожидания для дискретных и непрерывных случайных величин, получаем формулы для вычисления начальных моментов:

Определение 2.14. Центральным моментом порядка k случайной величины Х называется математическое ожидание k-й степени отклонения Х–М(Х), т.е.

Согласно определению математического ожидания случайной величины Х, получим следующие формулы для вычисления центральных моментов k-го порядка:

Следует отметить, что начальный момент первого порядка – это математическое ожидание, а центральный момент второго порядка – это дисперсия. Третий центральный момент служит характеристикой асимметрии ("скошенности") распределения. Для получения безразмерной характеристики делят на . Отношение называется коэффициентом асимметрии и обозначается . Если распределение симметрично относительно математического ожидания, то все моменты нечетного порядка равны нулю.

Если кривая плотности распределения непрерывной случайной величины такова, что справа от моды расположена ее "длинная часть", а слева – "короткая часть", то коэффициент S_k асимметрии положителен. Коэффициент асимметрии S_k отрицателен, когда "длинная часть" кривой плотности распределения расположена слева от моды. На рис. 2.13 показаны кривые плотности распределения с положительной и отрицательной асимметриями.

Рис. 2.13

Четвертый центральный момент является характеристикой "крутости", т.е. островершинности или плосковершинности распределения. Эти свойства описываются с помощью эксцесса, т. е. величины .

Число 3 вычитается из отношения , так как все распределения сравниваются с нормальным распределением, с которым мы познакомимся позже, для которого .

Кривые, более островершинные по сравнению с кривой закона нормального распределения, обладают положительным эксцессом. Кривые более плосковершинные – отрицательным эксцессом.

Пример 2.6. Продавец мороженого в солнечный день может, продать мороженого на 60 ден. ед. а в дождливый — на 20 ден. ед. Какова ожидаемая дневная выручка, если вероятность того, что день окажется дождливым, равна 0,35?

Решение. Ряд распределения случайной величины Х – возможная выручка в дождливый и солнечный дни имеет вид:

xi
pi	0,35	0,65

Так как Х - дискретная случайная величина и ожидаемая выручка – это математическое ожидание М(Х) = 20∙0,35+160∙0,65 = 7 +104 = 111, то продавец может продать мороженого на 111 ден. ед.

Среднее квадратическое отклонение ожидаемой выручки вычислим по формуле

Ответ:ожидаемая дневная выручка, равна 111 ден.ед.

Пример 2.7. Случайная величина задана плотностью распределения вероятностей:

Определить математическое ожидание и дисперсию этой случайной величины.

Решение. Используя формулу (2.9), вычисляем математическое ожидание:

(Для вычисления интеграла мы применили формулу интегрирования по частям).

По формуле (2.11) дисперсия

(Интеграл вычисляем дважды, применяя формулу интегрирования по частям).

Ответ:математическое ожидание равно 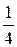, а дисперсия – 0,47.

Пример 2.8. Пусть случайная величина Z имеет вид . Найти математическое ожидание и дисперсию случайной величины Z.

Решение. Таккак случайная величии Х и число М(Х) независимы, то, воспользовавшись свойствами математического ожидания и дисперсии, можно записать:

так как , поскольку постоянная величина.

Ответ:математическое ожидание и дисперсия случайной величины Z, соответственно равны 0 и 1.

Случайные величины, для которых математическое ожидание равно нулю, а дисперсия равна единице, называются центрированными.

Вопросы для самопроверки

1.Что характеризует математическое ожидание случайной величины ?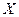

2.По каким формулам вычисляютсяматематические ожидания дискретной и непрерывной случайной величины ?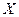

3.Перечислите другие числовые характеристики положения значений случайной величины .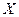

4.Докажите свойства математического ожидания случайной величины .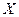

5.Укажите характеристики рассеяния значений случайной величины 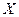и формулы для их вычисления.

6.Докажите свойства дисперсии случайной величины.

7.Сформулируйте определения начальных и центральных моментов и выпишите формулы для их вычисления.

8.Какие показатели характеризуют асимметрию и островершинность кривых распределений?