Независимость событий. Теорема умножения

Рассмотрим вероятностное пространство áW, F, Pñ, являющееся математической моделью вероятностного эксперимента.

Теорема 1.2.Вероятность совместного наступления двух событий равна произведению вероятности одного из них и условной вероятности другого при условии, что первое наступило:

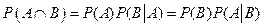(1.9)

Справедливость теоремы следует определения 1.5 и формул (1.7),(1.8).

Будем говорить, что наступление некоторого события A не зависит от события B при реализации некоторого эксперимента, если условная вероятность события A равна безусловной вероятности события A, то есть 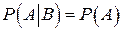. Но если событие A не зависит от события B, то и событие B не зависит от события A. Поэтому можно сформулировать следующее определение независимости двух событий.

Определение 1.6.Пусть áW, F, Pñ - вероятностное пространство некоторого эксперимента. События A Î , B Î называются независимыми, если

P(AÇB)= 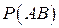= P(A)P(B), (1.10)

или другими словами, вероятность произведения двух независимых событий равна произведению вероятностей этих событий.

Смысл этого определения состоит в том, что если произошло одно из несовместных событий, то его появление не влияет на вероятность наступления другого события. Два события будем называть независимыми, если появление одного из них не меняет вероятности появления другого.

Кроме того, справедлива следующая теорема.

Теорема 1.3.Если события 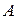и 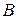независимы, то события 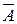и 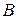также независимы.

Д о к а з а т е л ь с т в о. Пусть áW, F, Pñ - вероятностное пространство некоторого эксперимента и события A Î , B Î , 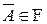. Представим событие 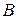в виде объединения двух несовместных событий: 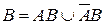. Тогда по аксиоме 3 Колмогорова 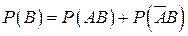, откуда 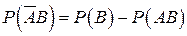. Но события 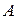и 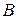независимы, следовательно, справедлива формула (1.10) и 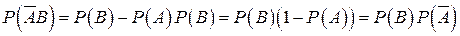, где 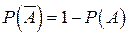. Теорема доказана.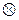

Следствие. Если события A и B независимы, то независимы также и события A 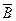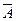и , и .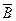

Пример 1.8.Пусть эксперимент состоит из двух подбрасываний симметричной монеты. Пространство элементарных событий 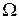рассматриваемого эксперимента включает следующие элементарные события: 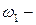при двух подбрасываниях выпало два герба; 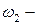в первом подбрасывании выпал герб, во втором – решетка; 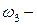в первом подбрасывании выпала решетка, во втором – герб; 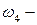при двух подбрасываниях выпало две решетки. Введем два события: A = { герб выпал при первом подбрасывании}, 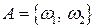,B = {решетка выпала при втором подбрасывании}, 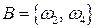. Вероятности этих событий по формуле (1.2) равны: 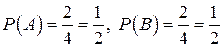. Событие 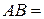{ герб выпал при первом подбрасывании, а решетка выпала при втором подбрасывании}, 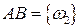. Его вероятность 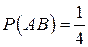. Произведение вероятностей событий А и В также равна 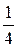. Следовательно, выполняется равенство (1.10): 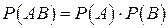, т.е. события А и В независимы.

На практике для определения независимости данных событий редко прибегают к проверке равенства (1.10) или эквивалентных ему равенств

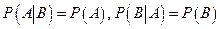. Обычно при этом пользуются интуитивными соображениями, основанными на опыте.

Теорема 1.2 обобщается для случая конечного числа событий 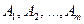, т. е. справедлива:

Теорема 1.4. Вероятность произведения событий A₁, A₂, …, A_m равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место:

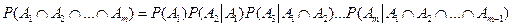. (1.11)

Д о к а з а т е л ь с т в о. Пусть áW, , Pñ - вероятностное пространство некоторого эксперимента и события A_i Î , .

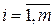Рассмотрим два события A₁ и A₂ с положительной вероятностью: 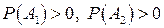. Из теоремы 1.2 следует, что 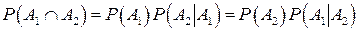. Предположим далее, что теорема справедлива для m – 1 события

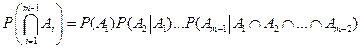
и докажем ее для m событий. Для этого введем обозначение 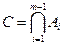. Тогда 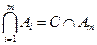и 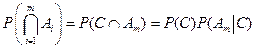по доказанному. По предположению .

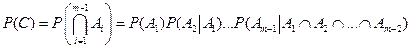Следовательно,

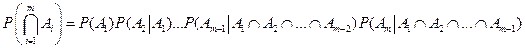, что и требовалось доказать.

Обобщим понятие независимости двух событий на совокупность нескольких событий.

Определение 1.7. События A₁, A₂, …, A_n называются независимыми в совокупности, если для любого события 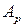из их числа и произвольных событий 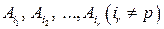из их числа, события 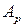и 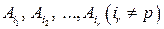взаимно независимы.

Для независимых событий в совокупности теорема умножения принимает вид:

Вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий:

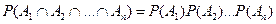или 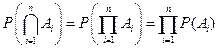. (1.12)

Заметим, что если имеется несколько событий A₁, A₂, …, A_n, то их попарной независимости (то есть независимости любых двух событий A_i и A_j, i¹j) недостаточно для независимости n событий в совокупности. Это иллюстрируется следующим примером С.Н. Бернштейна.

Пример 1. 9.На плоскость бросается тетраэдр. Три его грани окрашены в красный, синий и зеленый цвета, а на четвертую нанесены все три цвета.

Рассмотрим следующие события: 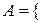при бросании тетраэдра на плоскость выпала грань, содержащая красный цвет 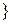; 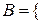при бросании тетраэдра на плоскость выпала грань, содержащая синий цвет 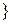; 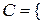при бросании тетраэдра на плоскость выпала грань, содержащая зеленый цвет .

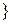Так как каждый из трех цветов имеется на двух гранях, то вероятности этих событий равны: 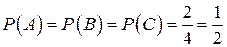. Любая пара цветов присутствует на одной грани, поэтому вероятность произведения любых двух событий 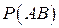= 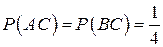. С другой стороны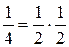 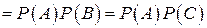= 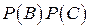, что означает попарную независимость событи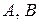й и 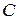. Три цвета присутствуют на одной грани, поэтому 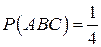, но произведение 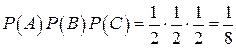. Следовательно, 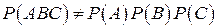, т.е. события А, В и С зависимы в совокупности.

Пример 1.10.В ящике 6 деталей завода № 1, 5 завода № 2 и 4 завода № 3. из ящика поочередно извлекают детали, не возвращая их обратно. Найти вероятность того, что при первом извлечении появится деталь завода № 3, при втором – деталь завода №2, при третьем – деталь завода №1.

Решение. Введем события 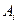= { при извлечении появится деталь i – го завода}, i = 1,2,3. События 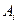зависимы. В результате извлечения деталей должно произойти событие 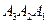, вероятность которого вычисляется по формуле (1.11), которая при 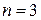принимает вид:

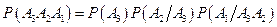. (1.13)

Вероятность появления детали изготовленной на заводе №3 вычисляется по классической формуле: 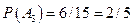. Вероятность появления детали, изготовленной на заводе №2, при втором извлечении, вычисляется в предположении, что при первом извлечении появилась деталь, изготовленная на заводе №3: 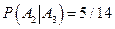. Вероятность появления детали, изготовленной на заводе №1, при третьем извлечении, вычисляется в предположении, что при первом извлечении появилась деталь, изготовленная на заводе №3, а при втором – деталь завода №2: т. е. условная вероятность 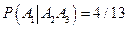. Подставив эти вероятности в формулу (1.13), получим:

.

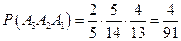Ответ: вероятность появления деталей в определенном порядке равна: .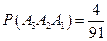

Пример 1.11. Рабочий обслуживает три станка. Вероятность того, что любой станок в течение часа потребует внимания рабочего, равна 0,4. Предполагая, что неисправности, возникающие на каждом из станков, независимы, вычислить вероятности того, что в течение часа потребуют внимания рабочего: 1) все три станка; 2) ни один станок; 3) по крайней мере один станок.

Решение. Введем события 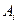= { в течение часа потребует внимания i – станок }, i =1,2,3. Из условия задачи следует, что эти события независимы. По теореме умножения вероятностей независимых событий вероятность того, что в течение часа все три станка потребуют внимания рабочего, т. е. произойдут события 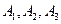одновременно, вычислим по формуле:

.

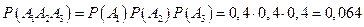Вероятность того, что в течение часа любой станок не потребует внимания рабочего, вычислим по правилу вычисления вероятности противоположного события:

.

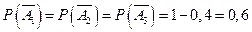Обозначим через событие 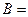{ни один станок в течение часа не потребует внимания рабочего}. Событие В произойдет, если произойдут события 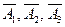одновременно, т. е. 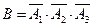. Вероятность этого события также вычисляется по формуле (1.12):

.

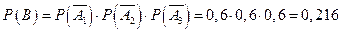Событие 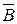, состоящее в том, что в течение часа по крайней мере один из трех станков потребует внимания рабочего, и событие В являются противоположными. Поскольку 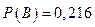, то

.

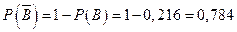Ответ: вероятность того, что в течение часа потребуют внимания рабочего: 1) все три станка 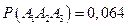; 2) ни один станок – 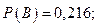3) по крайней мере один станок – .

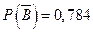Вопросы для самопроверки

1.Сформулируйте теорему о вероятности произведения двух событий.

2.Как определяется независимость двух событий?

3.Чему равна вероятность произведения двух независимых событий?

4. Равносильны ли понятия: попарная независимость и независимость в совокупности?

5.Сформулируйте теорему о вероятности произведения 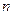событий.

6.Чему равна вероятность произведения 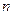независимых событий в совокупности?

7.Как найти вероятность хотя бы одного из 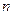независимых событий, имеющих одинаковые вероятности?

8.Доказать теорему умножения для независимых событий в совокупности.