Пространство элементарных событий

Любая наука, развивающая общую теорию какого-либо класса явлений, базируется на совокупности основных понятий, которыми она в дальнейшем оперирует.

Такими понятиями в теории вероятностей являются: эксперимент, элементарное событие, случайное событие, пространство элементарных событий.

Под экспериментом будем понимать осуществление намеченного действия и получение его результата. Результат эксперимента назовем исходом эксперимента. Следовательно, эксперимент состоит из выполнения некоторого действия и наблюдения за его результатом. Предметом наблюдения может быть какой-либо процесс, его часть или действующая система (в частности, экономическая).

Для проведения эксперимента необходимо создать определенную совокупность или комплекс условий s, которые предполагаются фиксированными и они либо существуют независимо от нас, либо создаются искусственно. Если при условиях s результат эксперимента предсказуем, то такой эксперимент называется детерминированным. Если при условиях s результат эксперимента непредсказуем, то такой эксперимент называется случайным.

Пример 1.1. Покупатели, подходящие случайным образом в разное время к кассе магазина, выстраиваются в очередь. Время, затраченное случайным покупателем на стояние в очереди, непредсказуемо.

Если случайный эксперимент будем многократно повторять при сохранении комплекса тех же условий s, то увидим, что множество его исходов подчиняется определенным закономерностям. Задача теории вероятностей состоит в установлении закономерностей, которым подчиняются результаты случайных экспериментов, обладающих статистической регулярностью.

Для построения и изучения математических моделей случайных экспериментов введем понятие пространства элементарных событий (исходов), соответствующего рассматриваемому эксперименту.

Само понятие пространства элементарных событий (исходов) математически является неопределяемым – оно исходно.

Пространством элементарных событий будем называть любое множество 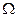взаимоисключающих исходов эксперимента такое, что каждый интересующий нас результат эксперимента может быть однозначно описан с помощью элементов этого множества.

Элементы пространства 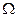обозначаются буквой 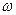и называются элементарными событиями (или элементарными исходами).

Пространство элементарных событий W будем считать заданным, если указаны все его элементы. Пространство W с конечным или счётным множеством его элементов будем обозначать соответственно 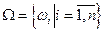и .

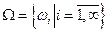Любое подмножество конечного или бесконечного пространства элементарных событий W называетсясобытием. События обозначаются прописными буквами латинского алфавита: 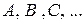Событие A произошло, если произошло какое-либо из элементарных событий w, принадлежащее A.

События A, B, C, ... происходят, если происходят какие-либо элементарные события, им принадлежащие. Однако, в результате реализации эксперимента элементарные события, способствующие появлению событий A, B, C, D, ..., могут, как произойти, так и не произойти. Такие события A, B, C, D, ... будем называть случайными.

Событие, содержащее все элементарные события данного эксперимента, называется достоверным и обозначается W. Достоверное событие – это событие, которое всегда происходит при выполнении данного комплекса условий s. Например, выпадение не более шести очков при подбрасывании игральной кости – достоверное событие, так как оно состоит из всех элементарных событий 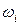– выпадение любого числа 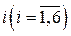очков из шести.

Событие, не содержащее ни одного элементарного события данного эксперимента, называетсяневозможным и обозначается Æ. Невозможное событиеÆ - это такое событие, которое не может произойти при выполнении комплекса условий s данного эксперимента. Например, выпадение числа очков больше шести при подбрасывании игральной кости – невозможное событие.

Таким образом, построение математического аппарата теории вероятностей начинается с описания пространства элементарных событий, которое может быть как конечным, так и бесконечным (счетным или несчетным).

Построение множества W осуществляется на практике, исходя из требования, чтобы все интересующие нас результаты данного эксперимента могли быть однозначно описаны на основе построенного множества W. Это означает, что множество W должно состоять из таких исходов эксперимента, чтобы существовали подмножества данного множества, равносильные событиям A, B, C,..., наблюдаемым в данном эксперименте.

В дальнейшем будем использовать следующие формы записи:

w Î A – элемент w принадлежит множеству A.

w Ï A – элемент w не принадлежит множеству A.

A Í W - множество 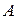есть подмножество W. В том случае, если A Í W, но A ¹ W, будем писать AÌ W.

A Î F – множество A есть элемент множества F.

Рассмотрим на примерах построение пространства элементарных событий.

Пример 1.2. Эксперимент состоит в подбрасывании один раз правильной шестигранной игральной кости. Опишем пространство элементарных событий W данного эксперимента.

Обозначим через X число очков, выпавших на верхней грани кости. В результате реализации эксперимента может произойти одно из следующих элементарных событий: 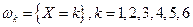. Тогда пространство элементарных событий W будет иметь вид:

.

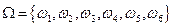Пример 1.3. Эксперимент состоит в наблюдении за продолжительностью ожидания пассажиром автобуса на остановке.

Если интервал движения автобусов не более 10 минут, то в качестве пространства элементарных событий можно взять множество:

,

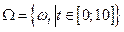элементарные события которого – это множества действительных чисел из отрезка [0; 10]: w_t = t, t Î [0; 10], t Î R.

Событие A, состоящее в том, что пассажир будет ожидать автобуса не более трех минут, состоит из множества действительных чисел отрезка [0, 3], то есть .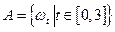

Если интервал движения автобусов неизвестен, то в качестве правой границы отрезка необходимо взять достаточно большое число, чтобы охватить все практически интересные ситуации.

Пример 1.4. Эксперимент состоит в подбрасывании монеты до тех пор, пока впервые не выпадет герб. После появления герба эксперимент прекращают.

Пусть 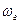и 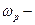означает выпадение герба и решетки соответственно. Элементарным исходом этого эксперимента является последовательность 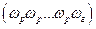. Таких последовательностей бесконечно много и все они различны. Следовательно, пространство элементарных событий этого эксперимента является бесконечным множеством.

Из примеров видно, что в самых простых экспериментах пространство элементарных событий W конечно, а в более сложных – бесконечно.

Вопросы для самопроверки

1.Что называют экспериментом?

2.Какие бывают эксперименты?

3. Какой эксперимент называется случайным?

4.Что называют элементарным событием?

5.Как обозначается элементарное событие?

6.Что называют пространством элементарных событий?

7.Как обозначается пространство элементарных событий?

8.Какое событие называют достоверным в данном эксперименте?

9. Какое событие называют невозможным в данном эксперименте?

10.Какое событие называют случайным в данном эксперименте?

11. Постройте пространство элементарных событий для эксперимента, состоящего в однократном подбрасывании двух игральных кубиков.