Соотношения между событиями.
Пусть задано произвольное, но фиксированное пространство элементарных событий W. Так как случайные события мы отождествляем с подмножествами пространства W, то операции над множествами позволяют ввести аналогичные соотношения между событиями.
Для более отчетливого уяснения соотношений между событиями будем пользоваться представлением пространства элементарных событий 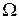 в виде некоторой области на плоскости. При этом, элементарные события
в виде некоторой области на плоскости. При этом, элементарные события 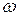 отождествим с выбором точки из этой области; события
отождествим с выбором точки из этой области; события 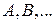 – отождествим с выбором точки в некоторой фигуре, лежащей внутри
– отождествим с выбором точки в некоторой фигуре, лежащей внутри 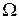 . Такие геометрические представления называются диаграммами Венна.
. Такие геометрические представления называются диаграммами Венна.
Для пояснения соотношений между событиями будем рассматривать эксперимент, состоящий в подбрасывании правильной шестигранной игральной кости. При каждом подбрасывании выпадает одна из граней, содержащая определенное число очков – от 1 до 6. Пространство элементарных событий этого эксперимента состоит из элементарных событий 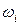 , где
, где 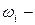 число очков, выпавших при одном бросании:
число очков, выпавших при одном бросании: 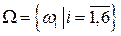 .
.
1. События А и В называются равными (или равносильными), А = В, если они состоят из одних и тех же элементарных событий.
Соответствующая диаграмма Венна представлена на рис. 1.1.
Например, при подбрасывании двух игральных костей равными будут события: А= {выпадение четной суммы очков} и B={на каждой грани выпадают очки одной четности}. События А и В одновременно происходят или оба не происходят.
2. Событие A влечет за собой событие B (пишут: 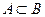 ), если событие B всегда происходит при появлении события A. Событие A состоит из элементарных событий, принадлежащих событию B.
), если событие B всегда происходит при появлении события A. Событие A состоит из элементарных событий, принадлежащих событию B.
Соответствующая диаграмма Венна представлена на рис. 1.1.
Для рассматриваемого эксперимента введем событие 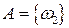 , а событие
, а событие 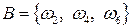 . Тогда при появлении события А произойдет и событие В, так как элементарное событие
. Тогда при появлении события А произойдет и событие В, так как элементарное событие 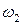 , входящее в событие А, входит и в событие В.
, входящее в событие А, входит и в событие В.
1.Объединением (суммой) двух событий A и В называется событие, обозначаемое 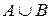 (А+В), состоящее в появлении события А или события В, или обоих событий вместе:
(А+В), состоящее в появлении события А или события В, или обоих событий вместе: 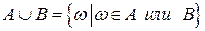 .
.
Иначе, событие 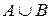 состоит в появлении хотя бы одного элементарного события, принадлежащего событию А, или событию В.
состоит в появлении хотя бы одного элементарного события, принадлежащего событию А, или событию В.
Соответствующая диаграмма Венна представлена на рис. 1.1.
Приведенное определение объединения распространяется на любое число событий. Объединением (суммой) конечной или счетной последовательности событий A1, A2, …, Ai, … называется событие C, состоящее в появлении хотя бы одного из элементарных событий, принадлежащих, по крайней мере, одному из событий 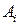 , и обозначаемое
, и обозначаемое 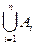 или
или 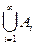 :
:
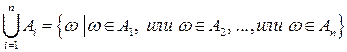 ,
, 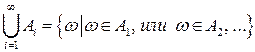 .
.
Для рассматриваемого эксперимента введем событие 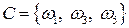 . Тогда
. Тогда 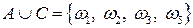 , т. е. событие
, т. е. событие 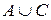 наступит, если выпадет грань, содержащая число очков равное или 1, или 2, или 3, или 5.
наступит, если выпадет грань, содержащая число очков равное или 1, или 2, или 3, или 5.
4. Пересечением (произведением) событий A и В называется событие, обозначаемое 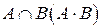 , состоящее в совместном появлении события А и события В. Событие
, состоящее в совместном появлении события А и события В. Событие 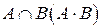 состоит из элементарных событий, принадлежащих и событию А и событию В:
состоит из элементарных событий, принадлежащих и событию А и событию В: 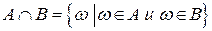 .
.
Соответствующая диаграмма Венна представлена на рис. 1.1.
Приведенное определение пересечения распространяется на любое число событий. Пересечением (произведением) конечной или счетной последовательности событий A1, A2, …, Ai, … называется событие, состоящее из элементарных событий, входящих в каждое из событий последовательности, и обозначаемое 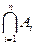 или
или 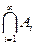 . Событие
. Событие 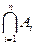 или
или 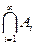 состоит в совместном выполнении всех событий, входящих в пересечение:
состоит в совместном выполнении всех событий, входящих в пересечение:
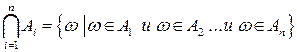 ,
, 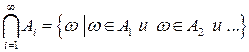 .
.
Для рассматриваемого эксперимента, событие 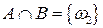 состоит в выпадении грани, содержащей число очков, равное 2.
состоит в выпадении грани, содержащей число очков, равное 2.
5. Противоположным по отношению к событию А называется событие 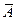 , состоящее в не появлении А и, таким образом, дополняющее его до W. Событие
, состоящее в не появлении А и, таким образом, дополняющее его до W. Событие 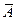 состоит из тех элементарных событий
состоит из тех элементарных событий 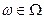 , которые не входят в событие А:
, которые не входят в событие А: 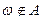 .
.
Событию 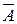 соответствует заштрихованная область на диаграмме Венна (рис. 1.1).
соответствует заштрихованная область на диаграмме Венна (рис. 1.1).
Для рассматриваемого эксперимента событие 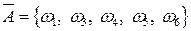 состоит из элементарных событий, не входящих в А.
состоит из элементарных событий, не входящих в А.
6. Разностью двух событий A и B называется событие A\B, состоящее из элементарных событий, которые принадлежат событию A, но не принадлежат событию B: 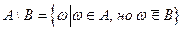 .
.
Событие 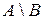 состоит в появлении события А, но не в появлении события В, т. е.
состоит в появлении события А, но не в появлении события В, т. е. 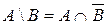 . Геометрическая иллюстрация на рис 1.1.
. Геометрическая иллюстрация на рис 1.1.
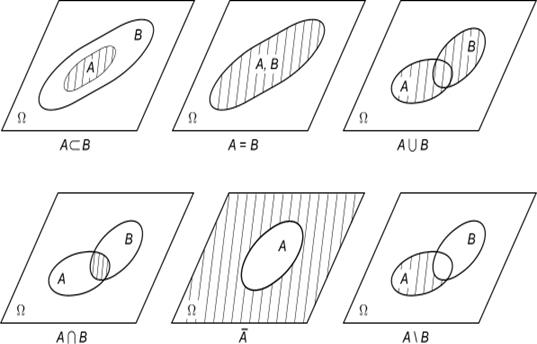
Рис. 1.1. Диаграмма Венна для рассмотренных соотношений между событиями.
7.Два события A и B называются несовместными, если у них нет общих элементарных событий, или события A и В не могут произойти одновременно: 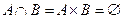 .
.
В рассматриваемом эксперименте события А и С несовместны.
8.События 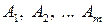 образуют полную группу событий если они:
образуют полную группу событий если они:
1) попарно несовместны (или просто несовместными) - появление любого из них исключает появление каждого из остальных 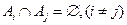 .
.
2) их сумма (объединение) есть достоверное событие: 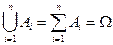 .
.
Операции объединения и пересечения меняются местами при переходе к противоположным событиям: 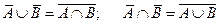 .
.
Замечание. Из сформулированных свойств событий следует, что:
1. Любое событие можно представить в виде объединения (суммы) двух несовместных событий: 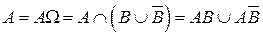 , где
, где 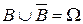 .
.
2. Если события 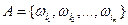 и
и 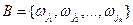 несовместны, то событие
несовместны, то событие 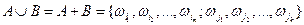 содержит m + k элементарных событий.
содержит m + k элементарных событий. 
Указанные соотношения между событиями применяются при построении вероятностной модели изучаемого эксперимента.
При построении вероятностной модели эксперимента необходимо определить:
1) пространство элементарных событий 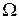 ;
;
2) класс событий, т.е. множество подмножеств 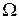 , которые будем рассматривать;
, которые будем рассматривать;
3) меру объективной возможности наступления событий из выделенного класса.
Построенный класс событий должен удовлетворять следующим условиям: 1) множество 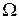 принадлежит этому классу; 2) если событие
принадлежит этому классу; 2) если событие 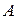 принадлежит классу, то и его противоположное событие
принадлежит классу, то и его противоположное событие 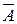 принадлежит классу; 3) если последовательность событий
принадлежит классу; 3) если последовательность событий 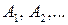 принадлежит классу, то и объединение событий
принадлежит классу, то и объединение событий 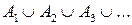 и их пересечение
и их пересечение 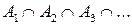 принадлежит этому классу.
принадлежит этому классу.
Класс событий, используемый в теории вероятностей и удовлетворяющий приведенным выше условиям, называется борелевским полем событий или 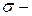 алгеброй и обозначается
алгеброй и обозначается  .
. 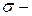 алгебры достаточно для описания любого экономического явления.
алгебры достаточно для описания любого экономического явления.
Класс событий, т.е. множество подмножеств 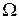 , удовлетворяющий следующим условиям: 1) множество
, удовлетворяющий следующим условиям: 1) множество 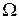 принадлежит этому классу; 2) если событие
принадлежит этому классу; 2) если событие 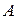 принадлежит классу, то и его противоположное событие
принадлежит классу, то и его противоположное событие 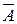 принадлежит классу; 3) если события
принадлежит классу; 3) если события 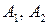 принадлежит классу, то и объединение событий
принадлежит классу, то и объединение событий 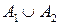 и их пересечение
и их пересечение 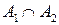 принадлежит этому классу, называется алгеброй событий и обозначаетсяА.
принадлежит этому классу, называется алгеброй событий и обозначаетсяА.
Таким образом, алгебра есть класс множеств, замкнутый относительно конечного числа операций дополнения, объединения и пересечения; s-алгебра есть класс множеств, замкнутый относительно счетного числа этих операций.
Если 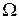 содержит конечное число элементарных событий, то класс событий
содержит конечное число элементарных событий, то класс событий  содержит не более
содержит не более 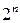 подмножеств.
подмножеств.
Пример 1.5.Рассмотрим эксперимент, состоящий в исследовании выполнения дневного задания двумя бригадами рабочих. Пространство элементарных событий 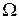 этого эксперимента состоит из трех элементарных событий:
этого эксперимента состоит из трех элементарных событий: 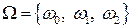 , где
, где 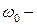 дневное задание выполнено двумя бригадами,
дневное задание выполнено двумя бригадами, 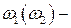 дневное задание выполнено одной бригадой (двумя бригадами). Класс всех подмножеств этого эксперимента состоит из
дневное задание выполнено одной бригадой (двумя бригадами). Класс всех подмножеств этого эксперимента состоит из 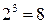 подмножеств:
подмножеств:
 =
= 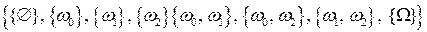 .
.
Так как подмножества 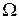 по определению являются событиями, то события
по определению являются событиями, то события 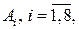 класса
класса  имеют следующий смысл:
имеют следующий смысл:
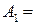
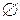 - невозможное событие не наступает при любой реализации эксперимента;
- невозможное событие не наступает при любой реализации эксперимента;
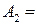
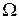 - достоверное событие наступает при любой реализации эксперимента;
- достоверное событие наступает при любой реализации эксперимента;
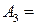
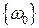 ={две бригады выполнили дневное задание};
={две бригады выполнили дневное задание};
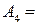
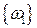 = { дневное задание не выполнено одной бригадой};
= { дневное задание не выполнено одной бригадой};
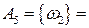 {дневное задание не выполнено двумя бригадами};
{дневное задание не выполнено двумя бригадами};
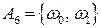 = {дневное задание выполнено двумя бригадами или дневное задание не выполнено одной бригадой}.
= {дневное задание выполнено двумя бригадами или дневное задание не выполнено одной бригадой}.
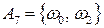 ={дневное задание выполнено двумя бригадами или дневное задание не выполнено двумя бригадами}.
={дневное задание выполнено двумя бригадами или дневное задание не выполнено двумя бригадами}.
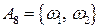 ={дневное задание не выполнено одной бригадой или дневное задание не выполнено двумя бригадами}.
={дневное задание не выполнено одной бригадой или дневное задание не выполнено двумя бригадами}.
Выполняя операции объединения и пересечения, над указанными в примере событиями 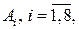 мы не выйдем за пределы класса
мы не выйдем за пределы класса  . Действительно,
. Действительно, 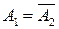 , или
, или 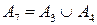 , или
, или 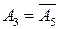 и т.д.
и т.д.
Вопросы для самопроверки
1. Какие события называют совместными в данном эксперименте?
2. Какие события называют несовместными в данном эксперименте?
3. Какие события называют противоположными?
4. Какие события называют равновозможными?
5. Какие события образуют полную группу событий?
6. Что представляет собой полная группа событий при подбрасывании
одной монеты?
7. Как определяется объединение (сумма) двух (или более) событий?
8. Как обозначают объединение (сумму) двух (или более) событий?
9. Приведите примеры объединения (суммы) двух событий.
10. Что называют пересечением (произведением) двух (или более) событий?
11. Приведите примеры пересечения двух событий.
12. Что называют разностью двух событий?
13. Приведите примеры разности двух событий.
14. Как можно представить любое событие?
15. Представьте соотношения между событиями при помощи диаграммы Венна.
16. Какие элементы определяются вначале при построении вероятностной модели случайного эксперимента?
17.Как определяется класс событий?
18.Какие события образуют 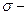 алгебру
алгебру  , алгебру А событий?
, алгебру А событий?
1.3. Вероятность. Методы вычисления вероятностей
Определение вероятности как функции множества.Пусть пространство элементарных событий 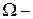 произвольное множество какого-либо эксперимента. Выделим систему подмножеств множества
произвольное множество какого-либо эксперимента. Выделим систему подмножеств множества 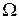 , образующих
, образующих 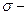 алгебру
алгебру  .
.
Если задано множествоW и 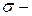 алгебра
алгебра  его подмножеств, то говорят, что задано измеримое пространство áW,
его подмножеств, то говорят, что задано измеримое пространство áW,  ñ.
ñ.
Для того, чтобы формализовать какую-либо вероятностную задачу, надо для соответствующего эксперимента построить измеримое пространство áW,  ñ, где W означает множество всех элементарных исходов эксперимента, а
ñ, где W означает множество всех элементарных исходов эксперимента, а 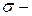 алгебра
алгебра  выделяет класс событий. Все остальные подмножества W, не входящие в
выделяет класс событий. Все остальные подмножества W, не входящие в  , событиями не являются.
, событиями не являются.
Выделение 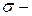 алгебры событий
алгебры событий  обусловлено, с одной стороны, существом рассматриваемой задачи, с другой стороны – природой множества W.
обусловлено, с одной стороны, существом рассматриваемой задачи, с другой стороны – природой множества W.
Значение неотрицательной функции 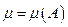 на
на 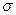 -алгебре множеств
-алгебре множеств  называется мерой, если она счетно-аддитивна, т. е. для счетного числа непересекающихся множеств
называется мерой, если она счетно-аддитивна, т. е. для счетного числа непересекающихся множеств 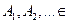
 и
и 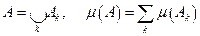 .
.
Определим на пространстве áW,  ñ числовую характеристику или вероятностную меру m(A) для измерения объективной возможности наступления события AÎ
ñ числовую характеристику или вероятностную меру m(A) для измерения объективной возможности наступления события AÎ  . (Значение неотрицательной функции
. (Значение неотрицательной функции 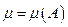 на
на 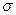 -алгебре множеств
-алгебре множеств  называется мерой, если она счетно-аддитивна, т. е. для счетного числа непересекающихся множеств
называется мерой, если она счетно-аддитивна, т. е. для счетного числа непересекающихся множеств 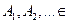
 и
и 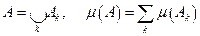 .Значение
.Значение 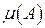 называется мерой множества
называется мерой множества 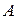 .) Эту числовую характеристику на множествах
.) Эту числовую характеристику на множествах 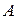 будем определять таким образом, чтобы она удовлетворяла условиям:
будем определять таким образом, чтобы она удовлетворяла условиям:
1. 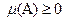 ;
;
2. 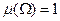 ;
;
3. 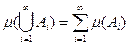 , в частности,
, в частности, 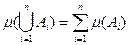 .
.
Функции множеств, удовлетворяющие условию 3, называются счетно-аддитивными ( 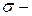 аддитивными) или, в частности, аддитивными мерами.
аддитивными) или, в частности, аддитивными мерами.
Определение 1.3Вероятностью события A называется числовая неотрицательная функция P(A), определенная на s-алгебре  измеримого пространства áW,
измеримого пространства áW,  ñ и удовлетворяющая следующим аксиомам:
ñ и удовлетворяющая следующим аксиомам:
Аксиома 1. Для любого события AÎ  вероятность события P(A) удовлетворяет неравенству:
вероятность события P(A) удовлетворяет неравенству: 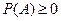 .
.
Аксиома 2. Вероятность наступления достоверного события W равна единице: P(W)=1.
Аксиома 3. Вероятность объединения счетного множества попарно несовместных событий 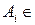
 ,
, 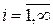 , (
, ( 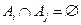 при
при 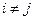 ), равна сумме их вероятностей:
), равна сумме их вероятностей:
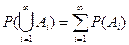 . (1.1)
. (1.1)
Эквивалентным аксиоме 3 будет требование аддитивности (1.1) для конечного числа событий 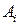 и следующая аксиома непрерывности.
и следующая аксиома непрерывности.
Аксиома 3'. Пусть последовательность {Bn} событий такова, что 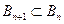 и
и 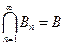 , тогда P(Bn) ® P(B) при n ®
, тогда P(Bn) ® P(B) при n ® 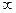 , т. е.
, т. е. 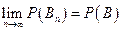 .
.
Из аксиом 1 – 3 следует, что вероятность P(A), определенная на множестве  , соответствует любому событию AÎ
, соответствует любому событию AÎ  и вероятность P(A), характеризующая степень объективной возможности наступления события A, представляет собой неотрицательную меру.
и вероятность P(A), характеризующая степень объективной возможности наступления события A, представляет собой неотрицательную меру.
Соответствие между событиями A множества событий  и их вероятностями называют распределением вероятностей на измеримом пространстве áW,
и их вероятностями называют распределением вероятностей на измеримом пространстве áW,  ñ.
ñ.
Тройка áW,  ,Pñ называется вероятностным пространством и задание вероятностного пространства есть задание счетно-аддитивной неотрицательной меры на измеримом пространстве, такой, что мера W равна 1.
,Pñ называется вероятностным пространством и задание вероятностного пространства есть задание счетно-аддитивной неотрицательной меры на измеримом пространстве, такой, что мера W равна 1.
В таком виде аксиоматика теории вероятностей была сформулирована А.Н. Колмогоровым.
Определение 1.4. Пространство элементарных событий W с выделенной в нем s-алгеброй  и определенной на измеримом пространстве вероятностной мерой P(A),
и определенной на измеримом пространстве вероятностной мерой P(A), 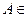
 , называется вероятностным пространством и обозначается áW,
, называется вероятностным пространством и обозначается áW,  ,Pñ.
,Pñ.
Построение вероятностного пространства áW,  ,Pñ является основным этапом при создании математической модели изучаемого эксперимента.
,Pñ является основным этапом при создании математической модели изучаемого эксперимента.
Если пространство элементарных событий 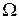 конечно или счетно, то распределение вероятностей можно определить вероятностями элементарных событий. В общем случае распределение вероятностей определяется функцией
конечно или счетно, то распределение вероятностей можно определить вероятностями элементарных событий. В общем случае распределение вероятностей определяется функцией 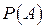 , заданной на элементах множества
, заданной на элементах множества  .
.
При введении понятия вероятности отмечалось, что каждому событию AÎ  соответствует количественная характеристика
соответствует количественная характеристика 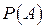 , называемая вероятностной мерой и характеризующая степень объективной возможности наступления этого события
, называемая вероятностной мерой и характеризующая степень объективной возможности наступления этого события 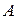 . Эта характеристика должна удовлетворять аксиомам Колмогорова. В определении не указывались способы задания вероятностной меры.
. Эта характеристика должна удовлетворять аксиомам Колмогорова. В определении не указывались способы задания вероятностной меры.
Под заданием вероятностной меры 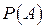 будем понимать правила определения вероятностей наступления некоторых базовых событий. Вероятности наступления других событий будут определяться по заданным вероятностям базовых событий, теорем и свойств вероятностной меры. При этом различные методы задания вероятностей будут характеризовать закономерности рассматриваемого вероятностного эксперимента.
будем понимать правила определения вероятностей наступления некоторых базовых событий. Вероятности наступления других событий будут определяться по заданным вероятностям базовых событий, теорем и свойств вероятностной меры. При этом различные методы задания вероятностей будут характеризовать закономерности рассматриваемого вероятностного эксперимента.
Классический (лапласовский) метод задания вероятности. Элементы комбинаторики. Рассмотрим случайный эксперимент, пространство элементарных событий которого содержит конечное число элементов w: 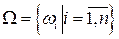 и все элементарные события wi равновозможны. Понятие равновозможности всех элементарных событий wi, i = 1, 2, .., n, означает, что в результате реализации эксперимента может произойти одно и только одно из n событий. Понятие равновозможности основано на симметрии условий эксперимента. Например, бросание симметричной монеты или симметричной игральной кости обладают симметрией, обеспечивающей равновозможность исходов. Как правило, такая симметрия присуща искусственно организованным экспериментам. Типичными примерами таких экспериментов являются азартные игры. С анализа таких игр и началось развитие теории вероятностей.
и все элементарные события wi равновозможны. Понятие равновозможности всех элементарных событий wi, i = 1, 2, .., n, означает, что в результате реализации эксперимента может произойти одно и только одно из n событий. Понятие равновозможности основано на симметрии условий эксперимента. Например, бросание симметричной монеты или симметричной игральной кости обладают симметрией, обеспечивающей равновозможность исходов. Как правило, такая симметрия присуща искусственно организованным экспериментам. Типичными примерами таких экспериментов являются азартные игры. С анализа таких игр и началось развитие теории вероятностей.
Несовместные и равновозможные элементарные события wiÎ W называют случаями, а об эксперименте говорят, что он сводится ксхеме случаев. Пусть W = { 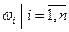 }, и все элементарные события равновозможны.
}, и все элементарные события равновозможны.
Зададим на W числовую неотрицательную функцию P такую, что 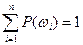 . Это значит, что функция P задает на W распределение вероятностей. Поскольку все элементарные события
. Это значит, что функция P задает на W распределение вероятностей. Поскольку все элементарные события 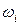 равновозможны и
равновозможны и 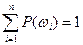 , то вероятности элементарных событий равны друг другу и равны
, то вероятности элементарных событий равны друг другу и равны 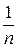 , т.е. P(w1) = P(w2) = … = P(wn) =
, т.е. P(w1) = P(w2) = … = P(wn) = 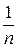 .
.
Этот метод задания вероятностей называется классическим или лапласовским.
При классическом методе задания вероятностей, вероятность любого события A Í W, 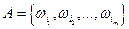 вычисляется по формуле
вычисляется по формуле
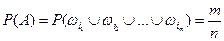 , (1.2)
, (1.2)
где 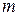 – число элементарных событий, входящих в A, а
– число элементарных событий, входящих в A, а 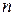 – общее число элементарных событий пространства W.
– общее число элементарных событий пространства W.
Таким образом, чтобы найти вероятность любого события A Í W, нужно подсчитать все элементарные события w, входящие в A, которые мы назовем благоприятствующими или благоприятными появлению событию A и все элементарные события, входящие в пространство W (все элементарные события являются равновозможными событиями).
Покажем, что функция 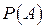 , определенная по формуле (1.2), удовлетворяет аксиомам 1 – 3 Колмогорова.
, определенная по формуле (1.2), удовлетворяет аксиомам 1 – 3 Колмогорова.
1. Для любого события 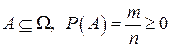 , так как
, так как 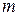 и
и 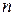 неотрицательные числа.
неотрицательные числа.
2. 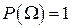 , так как
, так как 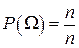 =1.
=1.
3. Если события 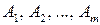 несовместны, то вероятность того, что произойдет хотя бы одно из этих событий, равна сумме их вероятностей, т.е.
несовместны, то вероятность того, что произойдет хотя бы одно из этих событий, равна сумме их вероятностей, т.е. 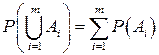 . Покажем это. Рассмотрим в пространстве элементарных событий
. Покажем это. Рассмотрим в пространстве элементарных событий 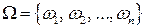 два события
два события 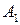 и
и 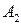 :
: 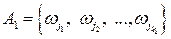 ,
, 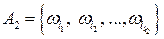 . Они не имеют общих элементарных событий, так как несовместны. Тогда по определению объединения событий, событие
. Они не имеют общих элементарных событий, так как несовместны. Тогда по определению объединения событий, событие 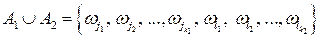 наступит, если произойдет хотя бы одно элементарное событие
наступит, если произойдет хотя бы одно элементарное событие 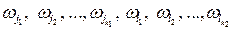 . Вероятность этого события, по формуле (1.2), равна
. Вероятность этого события, по формуле (1.2), равна 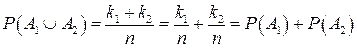 .
.
Предположим далее, что аксиома 3 справедлива для 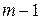 события, т. е.
события, т. е. 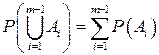 .
.
Вводя обозначение 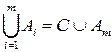 , где
, где 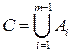 , и пользуясь доказанным утверждением для двух событий, получим:
, и пользуясь доказанным утверждением для двух событий, получим: 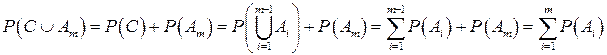 , что и требовалось доказать.
, что и требовалось доказать. 
Таким образом, при классическом определении вероятностей аксиомы Колмогорова выполняются.
Пример 1.6.На шахматную доску случайным образом ставят две ладьи – белую и черную. Какова вероятность того, что ладьи не побьют друг друга?
Решение. Пространство элементарных событий W состоит из элементарных событий 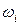 ={случайная расстановка двух ладей}. На шахматной доске 64 клетки. Поэтому число способов
={случайная расстановка двух ладей}. На шахматной доске 64 клетки. Поэтому число способов 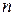 , расставить две ладьи, равно произведению
, расставить две ладьи, равно произведению 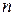 = 64´63 (первую ладью мы можем установить 64-мя способами, а вторую 63-мя способами, так как одна клетка будет занята).
= 64´63 (первую ладью мы можем установить 64-мя способами, а вторую 63-мя способами, так как одна клетка будет занята).
Пусть A – событие, состоит в том, что ладьи не побьют друг друга. Они не побьют друг друга, если не будут расставлены на одной линии. Поэтому, если первая ладья установлена, то из рассмотрения должны быть исключены 8 +7 = 15 клеток и, следовательно, для установки второй ладьи остается 49 клеток. Значит, событию A будут благоприятствовать 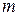 = 64´49 элементарных событий.
= 64´49 элементарных событий.
Воспользовавшись формулой (1.2), получим:
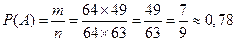 .
.
Ответ: вероятность того, что при случайной расстановке на доске две ладьи не побьют друг друга, составляет, примерно, 0,78.
Для вычисления числа элементарных событий m и n применяются формулы из области математики, называемой комбинаторикой.
Комбинаторика – раздел математики, посвященный решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствие с заданными правилами.
Каждое правило комбинаторики определяет способ построения некоторой конструкции из элементов исходного множества, называемой комбинаторной конфигурацией. Простейшими примерами комбинаторной конфигурации являются размещения, перестановки и сочетания.
Размещения. Множества, у которых указан порядок элементов, называют упорядоченными. Тогда множества, состоящие из одних и тех же элементов, но различающиеся порядком их расположения, будем считать различными. Например, если множество M состоит из трех элементов M = {a, b, c}, то можно образовать множества {a, b, c}, {a, c, b}, {b, a, c}, {b, c, a}, {c, a, b}, {c, b, a} , образованные из элементов a, b, c и отличающиеся друг от друга порядком их расположения. Размещением без повторений или просто размещением из n элементов по 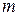 элементов называется упорядоченное множество, состоящее из
элементов называется упорядоченное множество, состоящее из 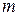 элементов с учетом их расположения. Размещения, состоящие из одних и тех же элементов, но различающиеся расположением элементов, считаются разными. Число размещений из n элементов по
элементов с учетом их расположения. Размещения, состоящие из одних и тех же элементов, но различающиеся расположением элементов, считаются разными. Число размещений из n элементов по 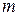 элементов вычисляется по формуле:
элементов вычисляется по формуле:
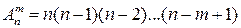 .
.
Например, чтобы определить, сколькими способами можно выбрать из 10 кандидатов 3 человека на 3 вакантные должности, нужно найти число размещений из 10 по 3. Тогда 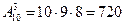 , то есть выбор из 10 кандидатов на три должности можно произвести 720 способами.
, то есть выбор из 10 кандидатов на три должности можно произвести 720 способами.
Пример 1.7. Рассмотрим эксперимент, состоящий в выборе без возвращений 4 букв из 10 первых букв русского алфавита и записи слова в порядке поступления букв. Какова вероятность того, что наудачу составленное слово будет оканчиваться буквой 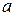 ?
?
Решение. Элементарное событие 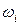 ={слово, составленное из выбранных букв},
={слово, составленное из выбранных букв}, 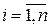 . Число всех слов равно числу упорядоченных множеств из четырех элементов, составленных из элементов множества, содержащего 10 элементов, то есть равно числу размещений:
. Число всех слов равно числу упорядоченных множеств из четырех элементов, составленных из элементов множества, содержащего 10 элементов, то есть равно числу размещений: 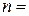
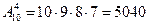 .
.
Введем событие A ={наудачу составленное слово из 4 букв оканчивается буквой 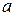 }. Число элементарных событий, благоприятствующих появлению события A, равно числу способов разместить на три оставшиеся места по одной букве из 9 оставшихся (буква
}. Число элементарных событий, благоприятствующих появлению события A, равно числу способов разместить на три оставшиеся места по одной букве из 9 оставшихся (буква 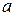 исключена из рассмотрения), то есть числу размещений:
исключена из рассмотрения), то есть числу размещений: 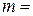
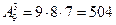 .
.
Воспользовавшись классической формулой (1.2), получим искомую вероятность:
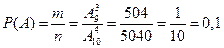 .
.
Ответ:вероятность того, что наудачу составленное слово будет оканчиваться буквой 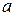 равна 0,1.
равна 0,1.
Если выбор 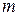 элементов из множества, состоящего из
элементов из множества, состоящего из 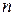 элементов, производится с возвращением и с упорядочением их в последовательную цепочку, то различными исходами будут всевозможные
элементов, производится с возвращением и с упорядочением их в последовательную цепочку, то различными исходами будут всевозможные 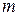 – элементные наборы, отличающиеся либо составом элементов, либо порядком их следования.
– элементные наборы, отличающиеся либо составом элементов, либо порядком их следования.
Полученные в результате множества называютсяразмещениями с повторениями, а их число определяется формулой 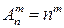 .
.
Пример 1.8. Пять человек вошли в лифт на первом этаже 9-этажного дома. Считая, что любой пассажир может с равной вероятностью выйти на 2-м, 3-м, ..., 9-м этажах, найти вероятность того, что все пассажиры выйдут на одном этаже.
Решение. Элементарное событие w данного эксперимента – комбинация выхода пяти пассажиров из лифта. Так как каждый пассажир может выйти из лифта на любом из 8-ми этажей независимо от другого, то он может выйти из лифта восемью способами. Столько же способов выйти из лифта существует для каждого пассажира. Поэтому число элементарных событий пространства W равно 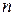 = 85.
= 85.
Пусть событие A = {все пассажиры выйдут на одном этаже}. Этому событию благоприятствуют 8 элементарных событий, так как они могут выйти на любом из 8-ми этажей. Тогда
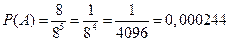 .
.
Ответ: вероятность того, что все пассажиры выйдут на одном этаже, равна 0,000244.
Перестановки. Перестановками из n элементов называются такие размещения из n элементов, которые различаются только расположением элементов. Число Pn перестановок из n элементов можно найти по формуле:
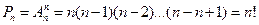 .
.
Например, число способов расположения 5 слушателей в ряду из 5 мест,
равно числу перестановок из 5 элементов:
P5 = 5! = 5×4×3×2×1 = 120.
Сочетания. Сочетаниями из n элементов по k элементов называются такие размещения, каждое из которых содержит k элементов и которые различаются по меньшей мере одним элементом. Число сочетаний из n элементов по k элементов вычисляется по формуле:
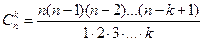 .
.
Сочетания, состоящие из одних и тех же элементов и различающиеся только их расположением, считаются эквивалентными, то есть из двух элементов 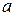 и
и 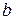 можно составить только одно сочетание (
можно составить только одно сочетание ( 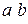 ). Тогда, если из каждого сочетания образовать все возможные перестановки, то получим все возможные размещения из
). Тогда, если из каждого сочетания образовать все возможные перестановки, то получим все возможные размещения из 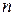 элементов по
элементов по 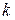 элементов:
элементов:
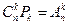 ,
,
откуда
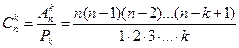 .
.
Можно доказать, что для сочетаний справедлива формула
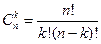 ,
,
которая во многих случаях упрощает процесс вычислений.
Свойства сочетаний.
1. 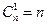 . 2.
. 2. 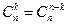 . 3.
. 3. 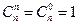 . 4.
. 4. 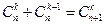 .
.
Пример 1.9. На оптовой базе имеется 40 телевизоров, среди которых 3 телевизора имеют некондиционные параметры. В розничную продажу отправляется 10 телевизоров. Найти вероятность того, что один из отобранных телевизоров не соответствует стандарту.
Решение. Пространство элементарных событий W состоит из 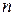 равновозможных событий
равновозможных событий 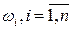 , где wi ={выбор 10 телевизоров из 40}. Число выборов 10 телевизоров из 40 определяется числом сочетаний
, где wi ={выбор 10 телевизоров из 40}. Число выборов 10 телевизоров из 40 определяется числом сочетаний 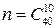 . Событие A ={выбор 10 телевизоров, из которых один некондиционный}. Для того, чтобы произошло событие A нужно один телевизор выбрать из 3 некондиционных и 9 из соответствующих стандарту. Число таких выборов определяется также числом сочетаний
. Событие A ={выбор 10 телевизоров, из которых один некондиционный}. Для того, чтобы произошло событие A нужно один телевизор выбрать из 3 некондиционных и 9 из соответствующих стандарту. Число таких выборов определяется также числом сочетаний 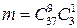 .
.
Воспользовавшись формулой (1.2), найдем вероятность события A:
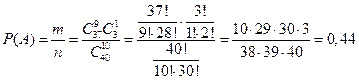 .
.
Ответ: вероятность того, что среди отобранных 10 телевизоров окажется один некондиционный, равняется P(A) = 0,44.
Если эксперимент состоит в выборе с возвращением m элементов множества, состоящего из n элементов, но без последующего упорядочения, то различными исходами такого опыта будут всевозможные m-элементные множества, отличающиеся составом. Получающиеся в результате данного эксперимента комбинации, называются сочетаниями с повторениями, и их число N определяется формулой:
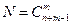 .
.
Пример 1.10. В библиотеке имеются книги по 20 разделам науки. Поступили
