Тема: Переход от алгебраической формы к показательной и тригонометрической, и обратно
Цель: Формирование навыков выполнения перехода от алгебраической формы комплексного числа к показательной и тригонометрической и обратно
Время выполнения: 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Запись комплексного числа 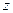 в виде
в виде 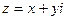 называется алгебраической формой комплексного числа. Переход от алгебраической формы записи к тригонометрической и обратно осуществляется по формулам
называется алгебраической формой комплексного числа. Переход от алгебраической формы записи к тригонометрической и обратно осуществляется по формулам
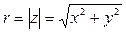 ; (25.1)
; (25.1)
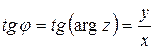 ; (25.2)
; (25.2)
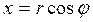 ; (25.3)
; (25.3)
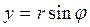 . (25.4)
. (25.4)
Для представления комплексного числа 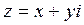 в тригонометрической форме необходимо найти: 1) модуль этого числа;
в тригонометрической форме необходимо найти: 1) модуль этого числа;
2) одно из значений аргумента этого числа. В силу многозначности 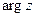 тригонометрическая форма комплексного числа также неоднозначна.
тригонометрическая форма комплексного числа также неоднозначна.
Формула Эйлера  устанавливает связь между тригонометрическими функциями и показательной функцией. Заменив в ней
устанавливает связь между тригонометрическими функциями и показательной функцией. Заменив в ней 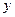 на
на 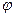 и на
и на 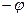 , получим
, получим
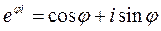 ;
; 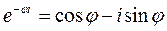 . (25.5)
. (25.5)
Складывая и вычитая эти равенства, получим
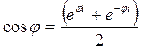 ;
; 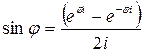 . (25.6)
. (25.6)
Эти две простые формулы, также называемые формулами Эйлера и выражающие тригонометрические функции через показательные, позволяют алгебраическим путем получить основные формулы тригонометрии.
Примеры
Задание 1: Представить в тригонометрической форме числа:
1) 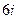 ; 2)
; 2) 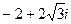 .
.
Решение: 1) Здесь 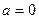 ,
, 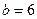 ,
, 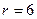 . Поскольку вектор, изображающий число
. Поскольку вектор, изображающий число 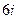 лежит на положительной полуоси
лежит на положительной полуоси 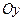 , главное значение аргумента
, главное значение аргумента 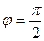 поэтому
поэтому
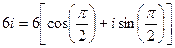
или
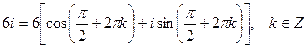 .
.
2) Здесь 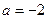 ,
, 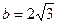 ,
, 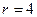 . Точка, изображающая число
. Точка, изображающая число 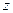 , лежит во II четверти;
, лежит во II четверти; 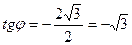 ,
, 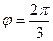 . Значит,
. Значит, 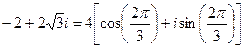
или
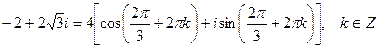 .
.
Задание 2: Представить в алгебраической форме числа:
1) 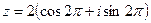 ; 2)
; 2) 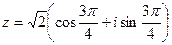 .
.
Решение: 1) Подставив значения 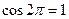 ,
, 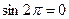 в данное равенство, получим
в данное равенство, получим  .
.
2) Имеем  .
.
Задание 3: Представить в показательной форме числа:
1) 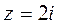 ; 2)
; 2) 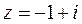 .
.
Решение: 1) Здесь 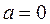 ,
, 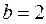 ,
, 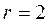 ,
, 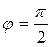 . По формуле
. По формуле 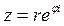 получим
получим 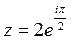 .
.
2) Здесь 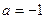 ,
, 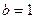 ,
, 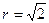 ,
, 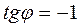 ,
, 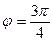 . По формуле
. По формуле 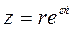 имеем
имеем 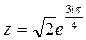 .
.
Задания для практической работы
1. Представьте в тригонометрической форме комплексные числа:
1) 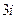 ; 2)
; 2) 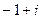 ; 3)
; 3) 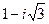 ;
;
4) 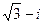 ; 5)
; 5) 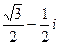 ; 6)
; 6) 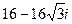 .
.
2. Представьте в алгебраической форме числа:
1) 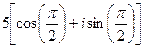 ;
;
2) 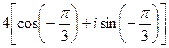 ;
;
3) 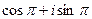 ;
;
4) 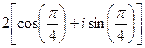 ;
;
5) 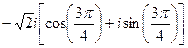 ;
;
6) 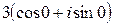 .
.
3. Представьте в показательной форме числа:
1) 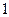 ; 2)
; 2) 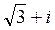 ; 3)
; 3) 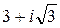 ;
;
4) 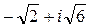 ; 5)
; 5) 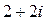 ; 6)
; 6) 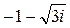 .
.
4. Представьте в алгебраической форме комплексные числа:
1) 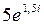 ; 2)
; 2) 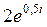 ; 3)
; 3) 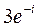 .
.
5. Найдите действительные числа 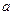 и
и 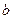 , такие, чтобы выполнялись равенства:
, такие, чтобы выполнялись равенства:
1) 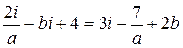 ;
;
2) 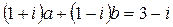 ;
;
3) 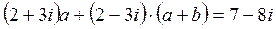 .
.
Контрольные вопросы:
1. Как осуществляется переход от записи комплексного числа, заданного в алгебраической форме, к его тригонометрической форме?
2. Как осуществляется переход от записи комплексного числа, заданного в тригонометрической форме, к его алгебраической форме?
3. Как осуществляется переход от записи комплексного числа, заданного в алгебраической форме, к его показательной форме и обратно?
Рекомендуемая литература: 1.2[с. 229-239].
СПИСОК ЛИТЕРАТУРЫ
1. Основная:
1.1 Богомолов, Н.В. Математика [Текст]: учебник для бакалавров / Н.В. Богомолов, П.И.Самойленко. - 5-е изд. - М.: Юрайт, 2014. - 396 с.
1.2 Богомолов, Н.В. Практические занятия по математике [Текст]: учебное пособие для бакалавров / Н.В. Богомолов. - 11-е изд. - М.: Юрайт, 2015. - 495 с.
1.3 Шипачев, В.С. Основы высшей математики: учебник и практикум/ В.С.Шипачев.-8-е изд. - М.: Юрайт, 2014. - 447 с.
2.Дополнительная:
2.1 Данко, П.Е., Высшая математика в упражнениях и задачах. В 2 ч. Ч.1: учеб. пособие для вузов / П.Е.Данко, А.Г. Попов, Т.Я. Кожевникова. – 8-е изд. – М.: ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и Образование», 2014. – 304 с.
2.2 Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2: Учеб. пособие для вузов / П.Е.Данко, А.Г. Попов, Т.Я. Кожевникова. – 8-е изд. – М.: ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и Образование»», 2014. – 416 с.
Учебное издание
ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ
Методические указания по выполнению практических работ
Составитель
