Тема: Решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
Цель: Формирование навыков решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
Время выполнения: 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Уравнение, содержащее производные (или дифференциалы) не выше второго порядка, называется дифференциальным уравнением второго порядка. В общем виде уравнение второго порядка записывается следующим образом:
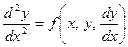 . (21.1)
. (21.1)
Общее решение дифференциального уравнения второго порядка содержит две произвольные постоянные.
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида:
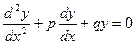 , (21.2)
, (21.2)
где 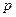 и
и 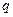 - постоянные величины.
- постоянные величины.
Для отыскания общего решения уравнения (21.2) составляется характеристическое уравнение
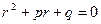 , (21.3)
, (21.3)
которое получается из уравнения (21.2) заменой 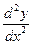 ,
, 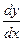 и
и 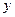 на соответствующие степени
на соответствующие степени 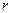 , причем сама функция
, причем сама функция 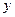 заменяется единицей.
заменяется единицей.
Тогда общее решение дифференциального уравнения (21.1) строится в зависимости от корней 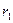 и
и 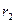 характеристического уравнения (21.3). Здесь возможны три случая.
характеристического уравнения (21.3). Здесь возможны три случая.
I случай: Корни 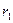 и
и 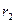 - действительные и различные. В этом случае общее решение уравнения (21.2) имеет вид
- действительные и различные. В этом случае общее решение уравнения (21.2) имеет вид
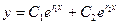 . (21.4)
. (21.4)
II случай: Корни 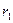 и
и 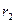 - действительные и равные:
- действительные и равные: 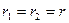 . Тогда общее решение уравнения (21.2) записывается так:
. Тогда общее решение уравнения (21.2) записывается так:
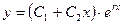 . (21.5)
. (21.5)
III случай: Корни 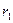 и
и 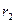 - комплексно – сопряженные:
- комплексно – сопряженные: 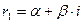 ,
, 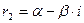 . В этом случае общее решение уравнения (21.2) записывается следующим образом:
. В этом случае общее решение уравнения (21.2) записывается следующим образом:
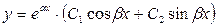 . (21.6)
. (21.6)
Примеры
Задание 1: Решить уравнение: 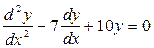 .
.
Решение: Составим характеристическое уравнение и найдем его корни: 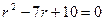 . Отсюда следует, что
. Отсюда следует, что 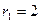 ,
, 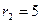 . Так как корни характеристического уравнения действительные и разные, то общее решение данного дифференциального уравнения согласно формуле (21.3) запишется так:
. Так как корни характеристического уравнения действительные и разные, то общее решение данного дифференциального уравнения согласно формуле (21.3) запишется так: 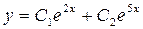 .
.
Задание 2: Найти частное решение уравнения 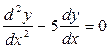 , если
, если 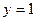 и
и 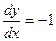 при
при 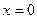 .
.
Решение: Составим характеристическое уравнение 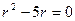 . Решая его, получим,
. Решая его, получим, 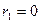 ,
, 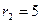 . Так как корни характеристического уравнения действительные и различные, то общее решение дифференциального уравнения имеет вид:
. Так как корни характеристического уравнения действительные и различные, то общее решение дифференциального уравнения имеет вид: 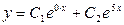 , то есть
, то есть 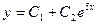 .
.
Для нахождения искомого частного решения нужно определить значения постоянных величин 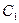 и
и 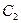 . Подставив в общее решение значения
. Подставив в общее решение значения 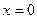 и
и 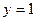 , получим
, получим 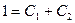 .
.
Продифференцировав общее решение и подставив в полученное выражение значения 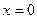 и
и 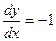 , имеем
, имеем 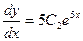 , отсюда следует, что
, отсюда следует, что 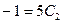 . Из данного выражения находим:
. Из данного выражения находим: 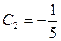 ,
, 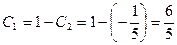 .
.
Таким образом, искомое частное решение имеет вид 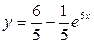 .
.
Задание 3: Решить уравнение 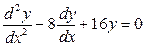 .
.
Решение: Составим характеристическое уравнение и найдем его корни: 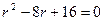 ,
, 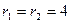 . Характеристическое уравнение имеет равные действительные корни; поэтому согласно формуле (21.5) общее решение данного дифференциального уравнения записывается в виде
. Характеристическое уравнение имеет равные действительные корни; поэтому согласно формуле (21.5) общее решение данного дифференциального уравнения записывается в виде 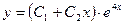 .
.
Задание 4: Найдите частное решение уравнения 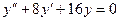 , если
, если 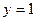 и
и 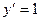 при
при 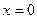 .
.
Решение: Так как характеристическое уравнение 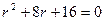 имеет равные действительные корни
имеет равные действительные корни 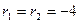 , то общее решение данного дифференциального уравнения записывается в виде
, то общее решение данного дифференциального уравнения записывается в виде
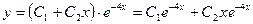 .
.
Дифференцируя общее решение, имеем
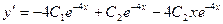 .
.
Подставив начальные данные в выражение для 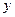 и
и 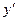 , получим систему уравнений
, получим систему уравнений
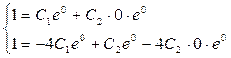 , или
, или 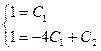 , откуда
, откуда 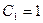 и
и 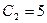 . Следовательно, искомое частное решение имеет вид
. Следовательно, искомое частное решение имеет вид 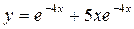 .
.
Задания для практической работы
1. Решите уравнения:
1) 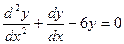 ;
;
2) 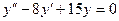 ;
;
3) 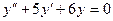 ;
;
4) 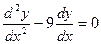 .
.
2. Найдите частные решения уравнений:
1) 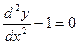 ;
; 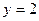 и
и 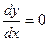 при
при 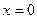 ;
;
2) 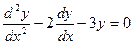 ;
; 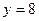 и
и 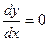 при
при 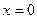 ;
;
3) 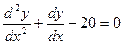 ;
; 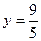 и
и 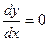 при
при 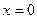 .
.
3. Решите уравнения:
1) 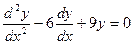 ;
;
2) 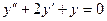 ;
;
3) 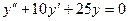 .
.
4. Найдите частные решения уравнений:
1) 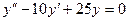 ;
; 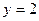 и
и 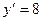 при
при 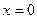 ;
;
2) 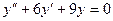 ;
; 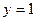 и
и 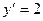 при
при 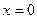 .
.
Вопросы для самоконтроля:
1. Какие дифференциальные уравнения называются уравнениями второго порядка?
2. Какие уравнения называются линейными однородными дифференциальными уравнениями второго порядка?
3. Какой вид имеет характеристическое уравнение? Для чего необходимо его нахождение?
4. Какие случаи возможны при нахождении общего решения дифференциального уравнения второго порядка?
Рекомендуемая литература: 1.2[с. 243-253], 2.2[с. 117-140].
Практическая работа №22
