Тема: Вычисление производных и дифференциалов высших порядков
Цель: Формирование навыков вычисления производных и дифференциалов высших порядков
Время выполнения: 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Производная второго порядка (вторая производная) от функции 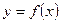 есть производная от ее первой производной:
есть производная от ее первой производной: 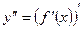 .
.
Производная третьего порядка (третья производная) от функции 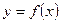 есть производная от ее второй производной:
есть производная от ее второй производной: 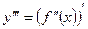 .
.
Производная n – го порядка (n – я производная) от функции 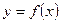 есть производная от ее (n – 1) – ой производной:
есть производная от ее (n – 1) – ой производной: 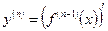 .
.
Дифференциал второго порядка (второй дифференциал) функции 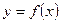 есть дифференциал от ее первого дифференциала:
есть дифференциал от ее первого дифференциала: 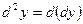 .
.
Дифференциал третьего порядка (третий дифференциал) функции 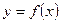 есть дифференциал от ее второго дифференциала:
есть дифференциал от ее второго дифференциала: 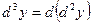 .
.
Дифференциал n – го порядка (n – ый дифференциал) функции 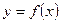 есть дифференциал от ее (n – 1) – ого дифференциала:
есть дифференциал от ее (n – 1) – ого дифференциала: 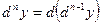 .
.
Примеры
Задание 1: Найти  ,
, 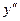 ,
, 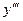 , …, если
, …, если 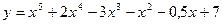 .
.
Решение: 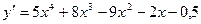 ,
,
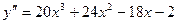 ,
,
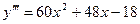 ,
,
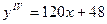 ,
, 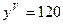 ,
, 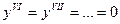 .
.
Задание 2: Найти дифференциалы первого, второго и третьего порядков функции 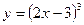 .
.
Решение: 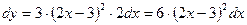 ,
,
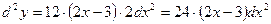 ,
,
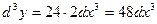 .
.
Задания для практической работы
1. Найдите производные второго порядка:
1) 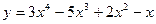 ; 2)
; 2) 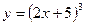 ; 3)
; 3) 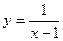 ; 4)
; 4) 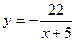 ;
;
5) 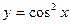 ; 6)
; 6) 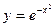 ; 7)
; 7) 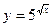 ; 8)
; 8) 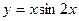 .
.
2. Найдите производные третьего порядка:
1) 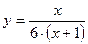 ; 2)
; 2) 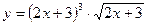 .
.
3. Найдите дифференциалы первого, второго и третьего порядков функций:
1) 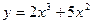 ; 2)
; 2) 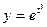 ; 3)
; 3) 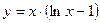 .
.
Контрольные вопросы:
1. Что называется производной второго порядка?
2. Что называется производной n – го порядка?
3. Что называется дифференциалом функции?
4. Что называется дифференциалом второго порядка?
5. Что называется дифференциалом n – го порядка? По какой формуле он вычисляется?
Рекомендуемая литература: 1.1[с. 236], 1.2[с.180-184],1.3[с. 276].
Практическая работа №13
Тема: Полное исследование функции. Построение графиков
Цель: Формирование навыков исследования функции и построения графиков
Время выполнения: 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Общая схема построения графиков функций
1. Найдите область определения функции.
2. Выясните, не является ли функция четной, нечетной или периодической.
3. Найдите точки пересечения графика с осями координат (если это не вызывает затруднений).
4. Найдите асимптоты графика функции.
5. Найдите промежутки монотонности функции и ее экстремумы.
6. Найдите промежутки выпуклости графика функции и точки перегиба.
7. Постройте график, используя полученные результаты исследования.
Пример
Построить график функции 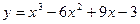 .
.
Решение:
1. Функция определена на всей числовой оси, то есть 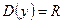 .
.
2. Данная функция не является ни четной, ни нечетной; кроме того, она не является периодической.
3. Найдем точку пересечения графика с осью  : полагая
: полагая 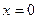 , получим
, получим 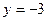 . Точки пересечения графика с осью
. Точки пересечения графика с осью  в данном случае найти затруднительно.
в данном случае найти затруднительно.
4. Очевидно, что график функции не имеет асимптот.
5. Найдем производную: 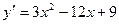 . Далее, имеем
. Далее, имеем 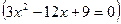
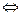
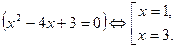 Точки
Точки 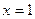 и
и 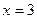 делят область определения функции на три промежутка:
делят область определения функции на три промежутка: 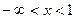 ,
, 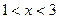 и
и 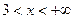 . В промежутках
. В промежутках 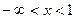 и
и 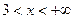
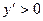 , то есть функция возрастает, а в промежутке
, то есть функция возрастает, а в промежутке 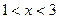
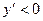 , то есть функция убывает. При переходе через точку
, то есть функция убывает. При переходе через точку 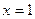 производная меняет знак с плюса на минус, а при переходе через точку
производная меняет знак с плюса на минус, а при переходе через точку 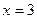 - с минуса на плюс. Значит,
- с минуса на плюс. Значит, 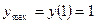 ,
, 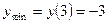 .
.
6. Найдем вторую производную: 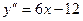 ;
; 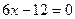 ,
,  . Точка
. Точка  делит область определения функция на два промежутка
делит область определения функция на два промежутка 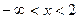 и
и 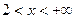 . В первом из них
. В первом из них 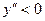 , а во втором
, а во втором 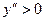 , то есть в промежутке
, то есть в промежутке 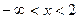 кривая выпукла вверх, а в промежутке
кривая выпукла вверх, а в промежутке 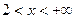 выпукла вниз. Таким образом, получаем точку перегиба
выпукла вниз. Таким образом, получаем точку перегиба 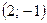 .
.
7. Используя полученные данные, строим искомый график (рис. 1).
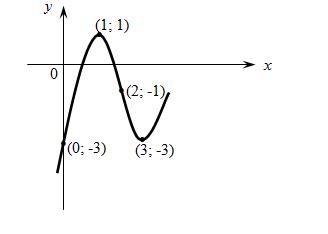
Рисунок 1 -График функции 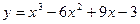 .
.
Задания для практической работы
Исследуйте следующие функции и постройте их графики:
1) 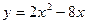 ; 2)
; 2) 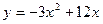 ;
;
3) 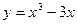 ; 4)
; 4) 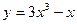 ;
;
5) 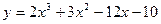 ; 6)
; 6) 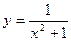 .
.
Контрольные вопросы:
1. Дайте определение возрастания и убывания функции.
2. Дайте определение экстремума функции.
3. Как найти наибольшее и наименьшее значения функции?
4. Сформулируйте определение асимптоты. Перечислите основные виды асимптот.
5. Сформулируйте общую схему исследования функции для построения графика.
Рекомендуемая литература: 1.1[с. 238-248], 1.2[с.180-184], 1.3[с. 310-325].
Практическая работа №14
